4.1.5.1 ECAH理论模型对纳米颗粒悬浊液的数值模拟
选取纳米二氧化钛-水、纳米铁-水悬浊液作为算例。计算中所用的物理参数见表4.3。
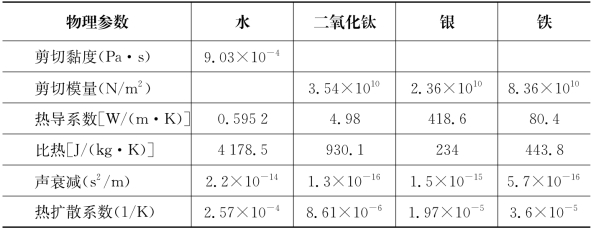
表4.3 水、二氧化钛、银和铁的物理参数(25℃)

(续表)
应用ECAH理论模型,对纳米级的二氧化钛、银、铁悬浊液进行了研究。图4.6a~c分别为直径20 nm的二氧化钛颗粒在浓度为1%~5%悬浊液中的衰减谱数值模拟结果、直径30 nm的铁在浓度为1%~5%悬浊液中的衰减谱数值模拟结果,以及直径为30 nm的银在浓度为1%~5%悬浊液中的衰减谱数值模拟结果。由图可以看出,声衰减始终随频率的升高而递增,同时这种递增趋势随浓度的增加而加剧。在颗粒粒度已知的情况下,通过测量两个频率下的声衰减系数就可以得到颗粒相的浓度。
图4.7a~c则是与图4.6a~c同等计算参数下所得到的声速与频率的关系图谱。与衰减明显不同的是,在纳米尺度下,单一尺寸纳米颗粒两相介质中的声速基本不随频率改变,而仅仅与浓度有关。这表明在单一尺寸纳米颗粒两相介质中,超声群速度与相速度数值相等,无频散特性。从图4.7可知,声速随颗粒相浓度增加而减小,在纳米颗粒粒度已知的情况下,只需测量颗粒两相介质中的声速便可确定颗粒相的浓度。
对不同频率下衰减和声速随颗粒尺寸变化的数值分析结果如图4.8、图4.9所示,悬浊液中的颗粒相体积浓度均为1%。由图4.8可以看出,声衰减随颗粒尺寸的增大而增加,这种变化趋势随超声频率的增加更加明显,表明在超声波纳米颗粒测量中,采用相对较高的检测频率,有利于获得更为丰富的频谱信息,这一点对直径小于20 nm的颗粒来讲更为重要。分析图4.8,考虑具有单一尺寸的纳米颗粒悬浊液,在忽略测量误差的情况下,只要测量其在一个波长下的声衰减并用上述模型进行数值分析,即可唯一地确定颗粒的大小。这一点与微米颗粒不同,后者至少需要测量三个波长下的声衰减系数,如果考虑测量中的误差因素,则可在更多波长下进行测量并进行数值分析,以确保所得到的颗粒尺寸是可靠的。
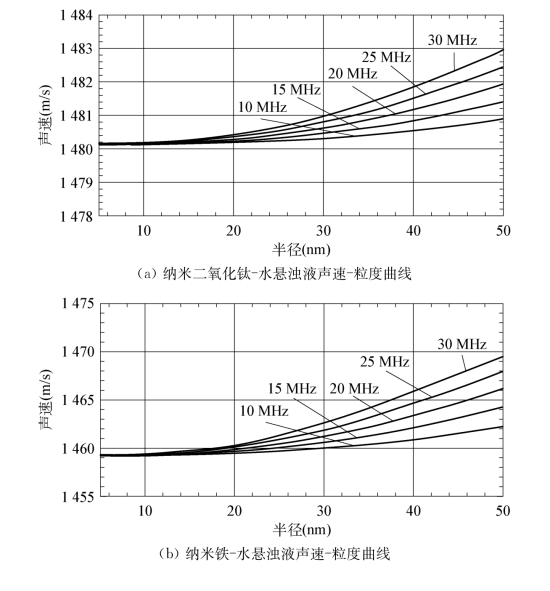
对相速度的研究则表明,当颗粒半径小于15 nm时,声速不随粒径大小改变,且群速度与相速度在数值上等同;当颗粒半径大于15 nm时,相速度随粒径增大而变大,该种变化趋势随频率的升高而变得明显,这意味着如要采用声速来测量粒径,只能有一个尺寸范围,该尺寸范围与被测颗粒的物理特性有关。
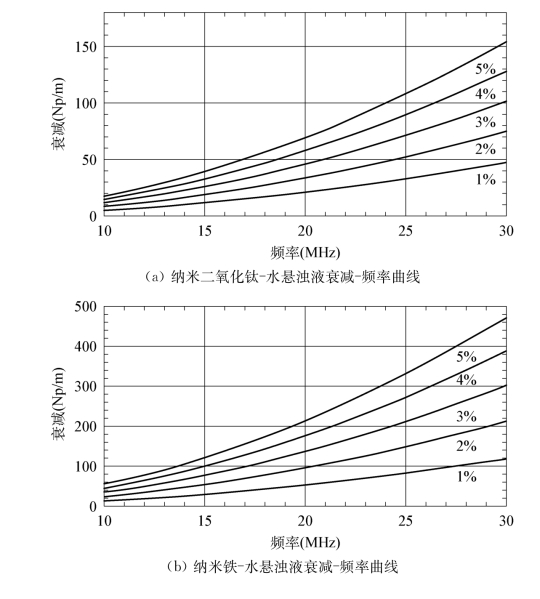
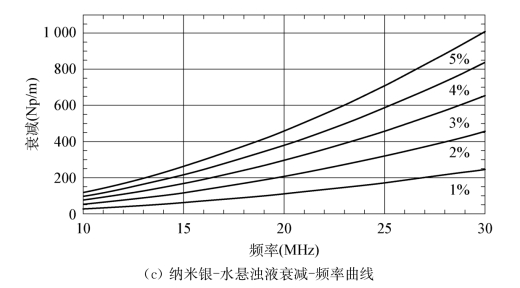
图4.6 纳米颗粒悬浊液的衰减-频率曲线
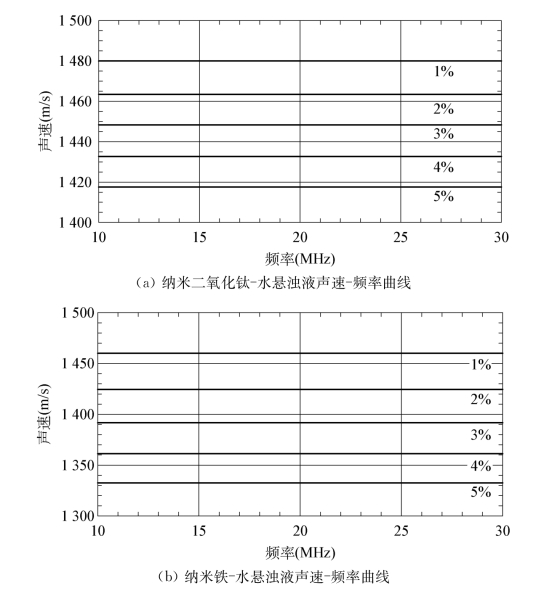
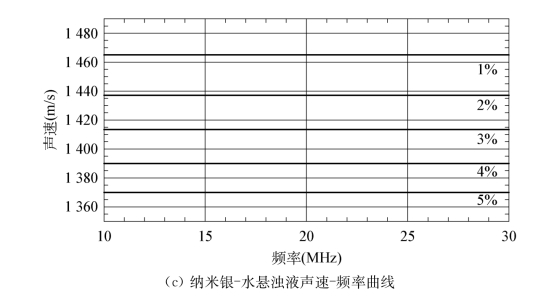
图4.7 纳米颗粒悬浊液的声速-频率曲线
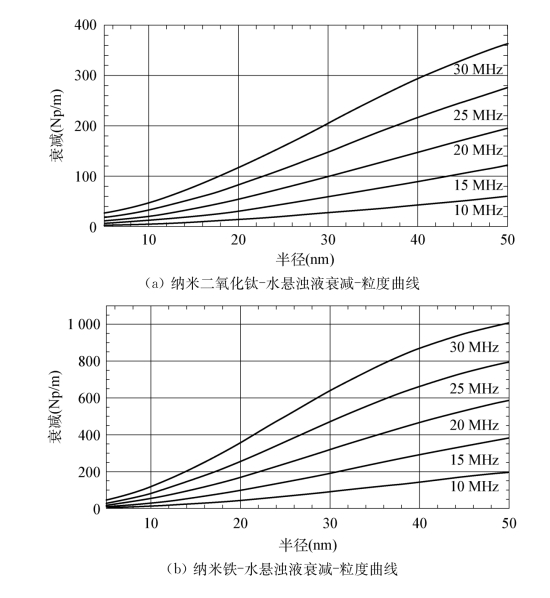
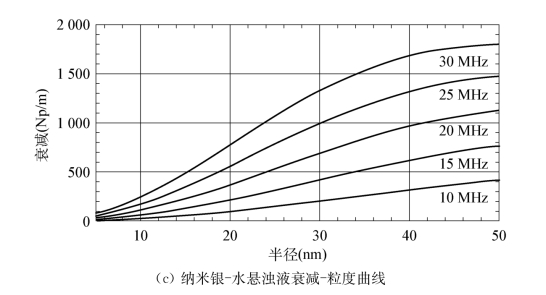
图4.8 纳米颗粒悬浊液的衰减-粒度曲线
 (https://www.xing528.com)
(https://www.xing528.com)
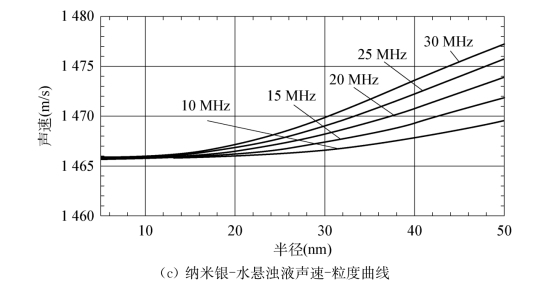
图4.9 纳米颗粒悬浊液的声速-粒度曲线
4.1.5.2 McClements理论模型叠加BLBL理论模型对纳米颗粒悬浊液的数值模拟
选取纳米玻璃珠-水悬浊液作为算例。分析图4.10,在“长波长”的情况下,ECAH理论模型与McClements理论模型叠加BLBL理论模型所做的算例吻合较好,尤其衰减曲线完全吻合,因此在低浓度(一般低于5%)情况下的超声衰减谱纳米颗粒粒度分布测量中完全可以由后者替代前者。在声速曲线中,ECAH理论模型与McClements理论模型叠加BLBL理论模型所做的数值分析相差低于4 m/s,因此在结合不同理论模型利用相速度测量纳米颗粒粒度分布时,只需做数值上的修正即可。
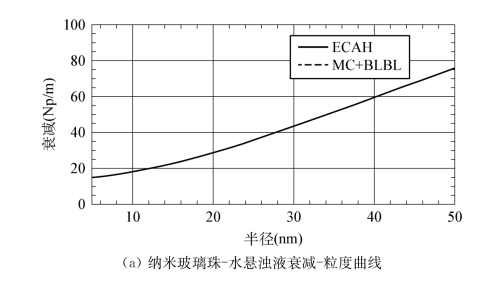
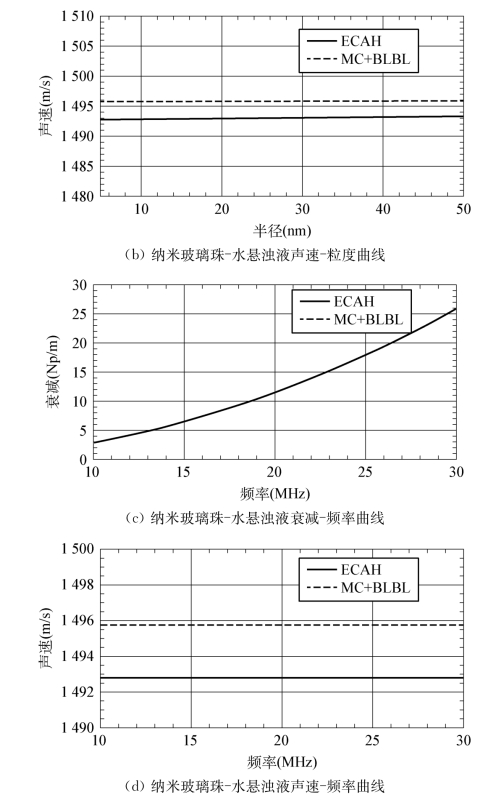
图4.10 ECAH理论模型与McClements+BLBL理论模型的对比
4.1.5.3 ECP理论模型对纳米颗粒悬浊液的数值模拟
选取纳米二氧化钛-水、纳米银-水悬浊液作为算例。计算所使用的物理参数见表4.3。
图4.11中数值模拟所用颗粒相体积浓度均为30%。从图中可以看出,当颗粒直径小于20 nm时,在30 MHz频段范围内,超声衰减对频率的改变相对不明显,意味着利用ECP理论模型检测高浓度状态下,低于20 nm的高密度差异纳米颗粒需要采用高频超声波检测更有利于获得所需信息。
图4.12中数值模拟所用均为单一粒径30 nm。从图中可以看出,声衰减基本随频率线性增加,这种增加趋势随体积浓度的升高而更加明显,这证明在已知颗粒尺寸的情况下,通过测量两个频率下的衰减值就可确定高密度差异颗粒两相介质中的颗粒相浓度。与ECAH理论模型对比可以发现,在高浓度情况时,相同超声频率下,相同体积浓度间隔,其衰减增量完全不同,表明此时声衰减并不是颗粒系中不同颗粒衰减的简单叠加,颗粒间相互作用所造成的声能损失已经显现。
图4.13中数值模拟所用颗粒相体积浓度为30%。高浓度情况时,同样存在越高检测频率声衰减的变化越明显,考虑具有单一尺寸的颗粒悬浊液,如果待测颗粒系的体积浓度为未知数,则在ECP理论模型复波数计算公式中便存在超声衰减系数α、待测颗粒半径a、颗粒相体积浓度ψ三个未知数。因此运用ECP理论模型,仅需要测量两个波长情况下的超声衰减系数便可唯一确定出颗粒的大小。如果考虑测量误差影响,则需要测量更多波长情况下的超声衰减,以得到较高的测量精度。
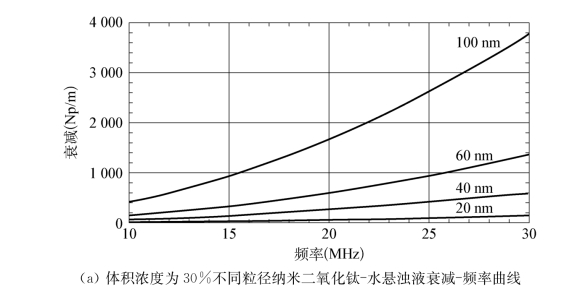
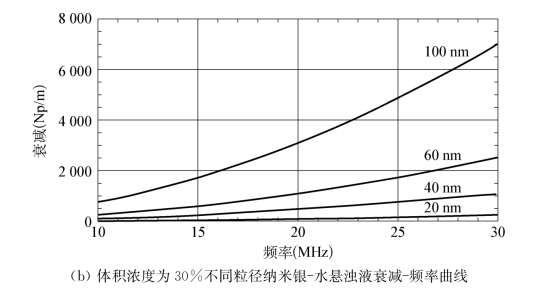
图4.11 特定体积浓度不同粒径纳米颗粒悬浊液衰减-频率曲线
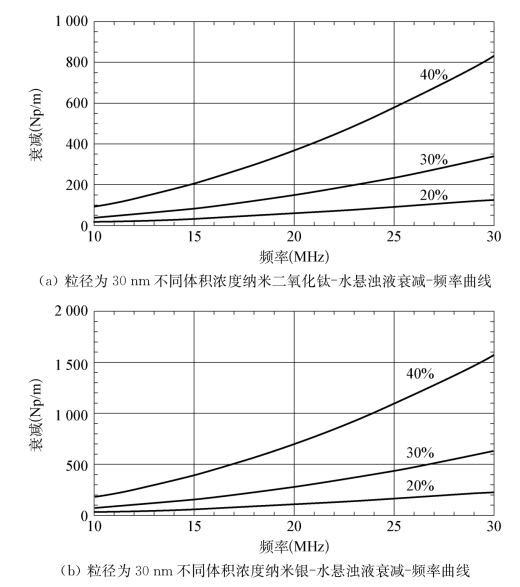
图4.12 特定粒径不同体积浓度纳米颗粒悬浊液衰减-频率曲线
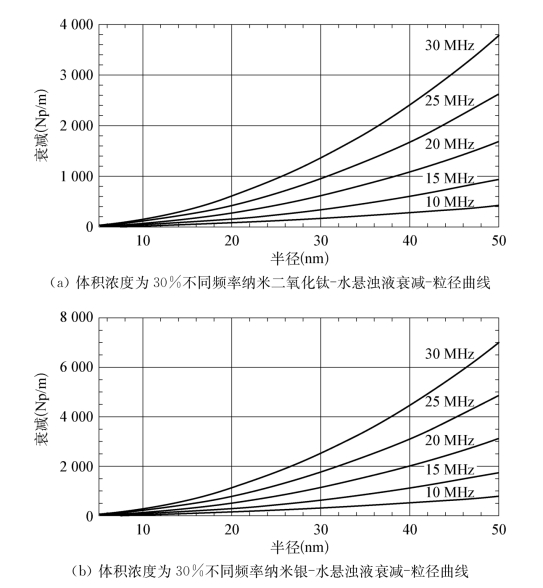
图4.13 特定体积浓度不同频率纳米颗粒悬浊液衰减-粒径曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




