在前面所提及的超声谱测量技术中,脉冲反射式是最为常见的测量手段,相较于其他测量方法,脉冲反射式的检测成本较低,检测技术容易实现。接下来重点分析短时傅里叶变换技术在脉冲反射式超声衰减谱与相速谱测量中的应用。
如前所述,通常情况下为获得超声衰减谱与相速谱,首先对超声波时域信号做快速傅里叶变换(fast Fourier transform,FFT),快速建立起时域和频域信号的联系。但是该技术仅可以测量纳米颗粒两相介质中的超声衰减谱,如果要测量两相介质中的相速谱还需要借助其他技术完成。而采用短时傅里叶技术,可以同时对超声信号进行时频处理,是一种快速、准确获取颗粒两相介质中超声衰减谱与相速谱的方法。
3.2.3.1 短时傅里叶变换
短时傅里叶变换的实质是一种加窗后的移动傅里叶变换,假设有一信号s(t),其短时傅里叶变换的定义如下:
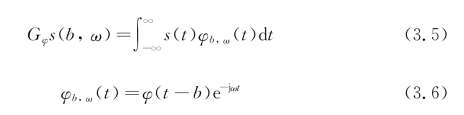
其中,![]() 。
。
式中 ψ(t)——窗函数,其定义由下式给出:
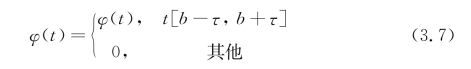
式中 b——某特定时刻;
τ——该时刻的时间窗宽度;
ω——角频率。
根据式(3.5)~式(3.7),在某特定时刻b,用宽度为2τ的时间窗截取信号s(t),对得到的信号进行快速傅里叶变换,即可获得信号s(t)在特定时刻b的幅度谱,将时间窗后移,依次进行相同操作,最终可得到某一特定频率下的信号在整个信号有效时间内的幅度谱。图3.8a、b分别为中心频率5 MHz的超声波信号以及对信号进行短时傅里叶变换后的幅度谱。
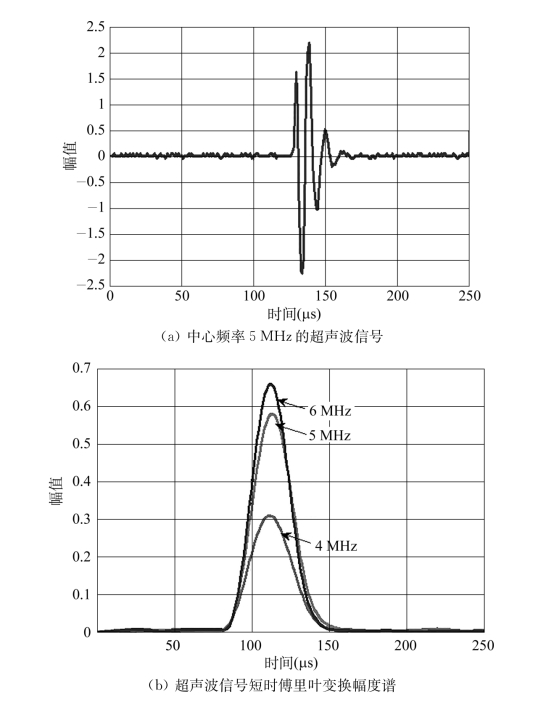
图3.8 超声波信号及其短时傅里叶变换幅度谱
在短时傅里叶变换中,时间窗函数以及窗函数宽度如何确定关系到最终的测量结果准确与否,不同类型的窗函数具有不同的频率特性,窗函数的宽度选择应该兼顾时间与频率分辨率。
1)窗函数选择
现有两列声程不一但完全相同的超声波信号,中心频率5 MHz,信号长度为0.368μs(时长92个采样点,采样频率250 MS/s),两信号前沿相距1.756μs(时长439个采样点),分别采用宽度100个采样点的不同窗函数,对两列超声波信号做短时傅里叶变换。图3.9为5 MHz单频超声波信号的时间-幅值变化关系。
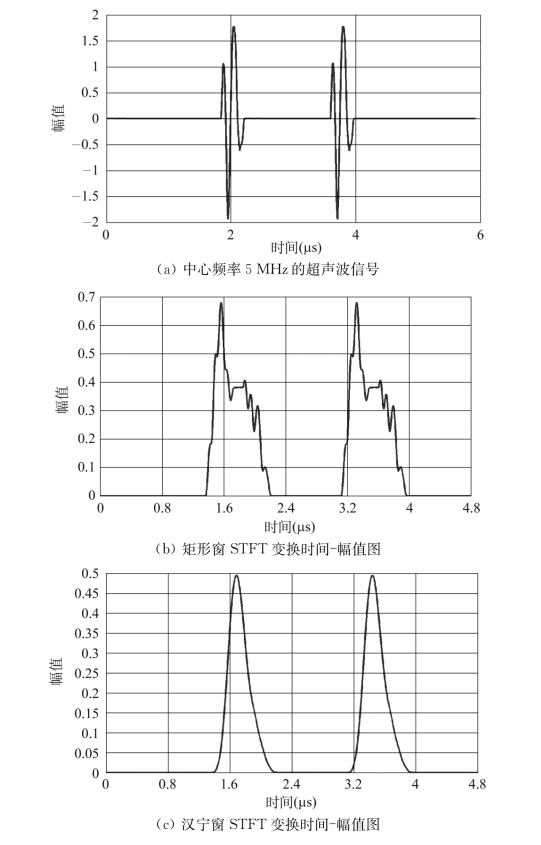
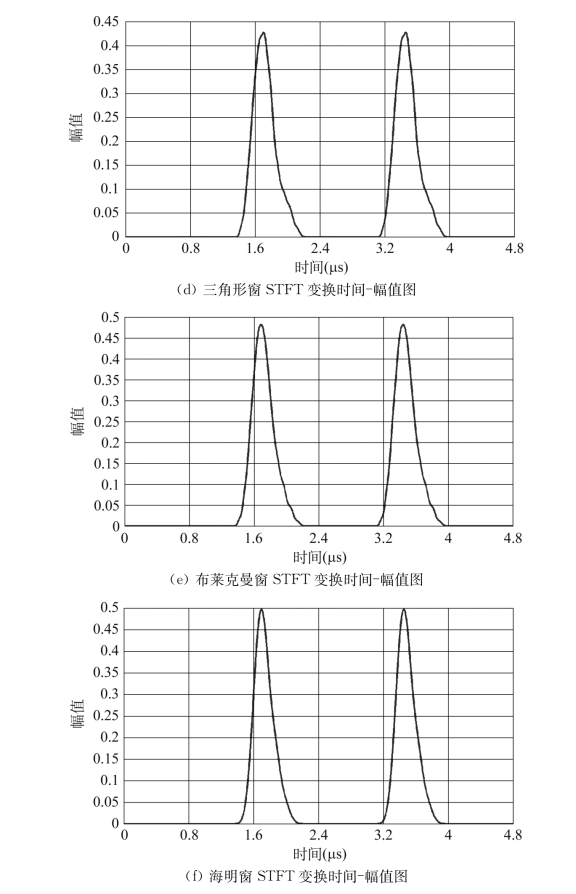
图3.9 中心频率5 MHz超声波信号及其不同窗函数STFT变换时间幅值图
根据图3.9,矩形窗函数用于短时傅里叶变换后的信号顺滑度很差,变换后的信号严重粗糙,无法确定信号的峰值,可以舍弃。汉宁窗函数、海明窗函数、布莱克曼窗函数以及三角形窗函数短时傅里叶变换后所得到的信号光滑度较好,有利于信号峰值的确定。图3.9c、d、e、f中,信号处理后所得两列信号的峰值坐标见表3.1。
表3.1 不同窗函数短时傅里叶处理结果
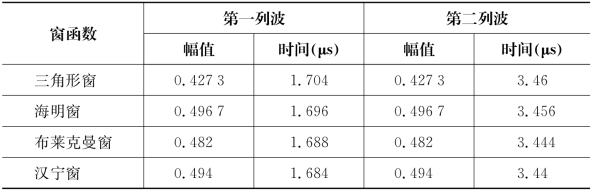
从表3.1中可以看出,将上述四种窗函数用于短时傅里叶变换后所得的前后两列单频信号幅值完全相同,而时间差分别为1.756μs、1.76μs、1.756μs、1.756μs,差别为0.004μs(差别1个采样点),对相速度的影响甚微,可以忽略。从四种窗函数所得单频信号的幅值比较看,海明窗函数所得单频信号幅值最大,因此相对而言更适合于超声衰减谱与相速谱的测量。
2)窗函数宽度选择
短时傅里叶变换的本质就是傅里叶变换的移动窗处理,按照式(3.5)~式(3.7),计算处理后的局部频谱为G(f-f0)ej2πft。其中,G(f)为分析窗函数ψ(t)的频谱,而单频信号的局部特征包含在相位因子ej2πft里面。由此可见,局部频谱被分析频谱展宽。因此随着窗函数的宽度变窄,局部频谱会变宽,此时会降低局部频谱的频率分辨率;为增加局部频谱的频率分辨率,需要将窗函数的宽度展宽,以减小分析频谱的宽度。但随着窗函数宽度的增加,时间分辨率会下降,因此必须在频率分辨率与时间分辨率之间寻找一个合适的窗函数宽度。
将海明窗函数用于短时傅里叶变换,选取不同窗函数宽度对图3.9a的超声波信号做信号处理,得到多个不同频率信号的时间-幅值谱,如图3.10所示。
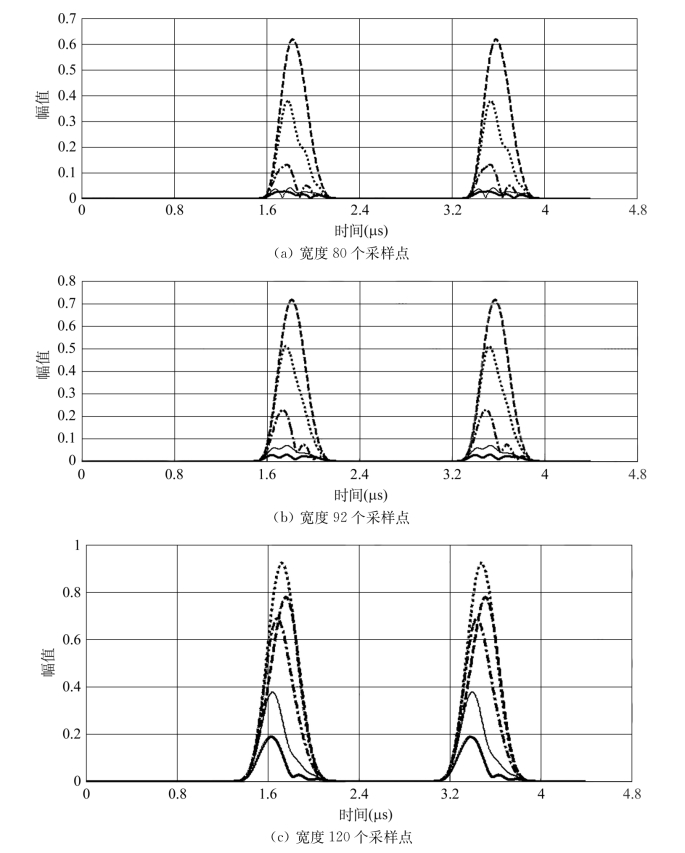
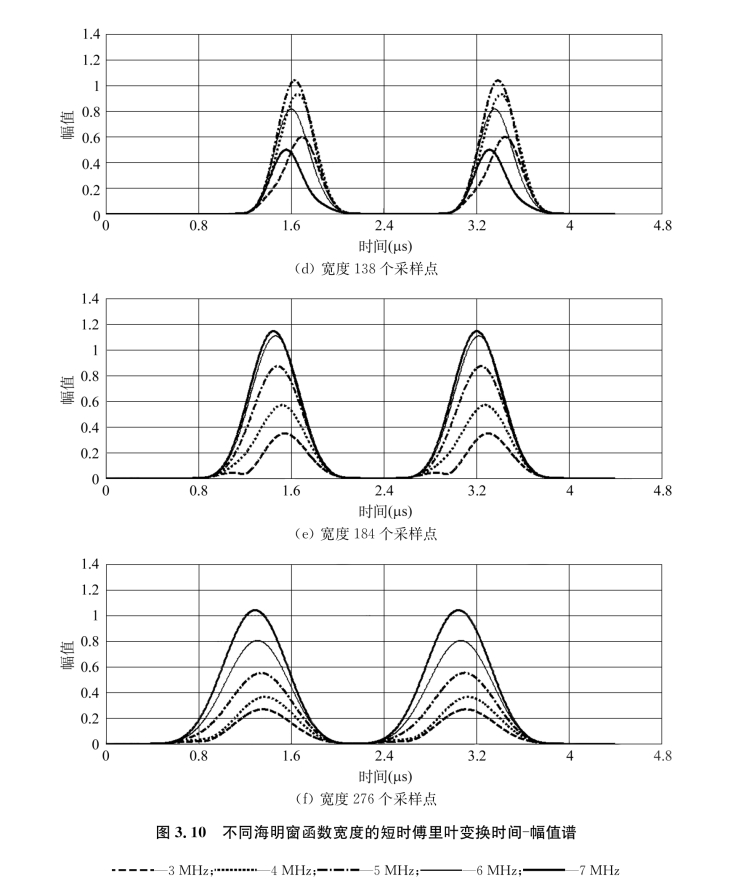
图3.10 不同海明窗函数宽度的短时傅里叶变换时间-幅值谱
从图3.10a、b中可以看出,如果超声波信号长度大于或等于窗函数宽度,则短时傅里叶变换后的时间-幅值谱对频率的分辨率较差,图中6 MHz和7 MHz单频信号的峰值不能够准确定位;在图3.10c中,当窗函数宽度为超声波信号长度的1.3倍时,短时傅里叶变换后的时间-幅值谱对频率的分辨率有所改善,图中6 MHz与7 MHz单频信号的峰值已经较好地分辨出;继续加大窗函数宽度,则出现高频信号幅值增加,而低频信号幅值降低以及所有单频信号时间-幅值谱展宽的现象。按照图3.10e、f,当窗函数宽度大于超声波信号长度的2倍时,在3 MHz、4 MHz、5 MHz、6 MHz、7 MHz所有单频信号的时间-幅值谱中,存在多点幅值同时处于最大值的情况,这意味着对时间的分辨率较差;对比图3.10c、d,图3.10d中所显示的信号幅值大小以及信号的光滑程度明显好于图3.10c中所显示的信号。因此可以得出这样一个结论,即短时傅里叶变换中窗函数宽度的最优值应该为待分析时域信号长度的1.5倍左右。
3.2.3.2 相位谱法测量相速谱
在已知声程长度X的情况下,通过测量前后两列超声回波信号中各不同频率分量信号的相位差,该相位差与对应角频率的比值便是角频率为ω的超声波在声程长度为2X的距离内传播所经过的时间:
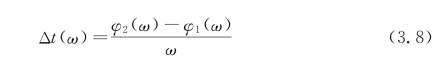
式中 ∆t(ω)——声时;(https://www.xing528.com)
ψ2(ω)——第二次超声回波信号的相位;
ψ1(ω)——第一次超声回波信号的相位;
ω——超声波角频率。
某单一频率ω的超声波信号在颗粒两相介质中的相速度计算由下式获得:

需要指出,计算机得出的超声波信号相位始终是[-π,π]内的相位主值,必须将其转换为连续相位,即实现信号的相位展开,具体如图3.11所示。
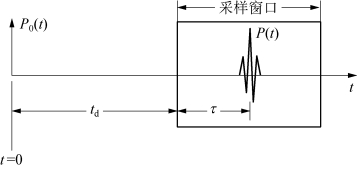
图3.11 相位展开示意图
图3.11中,t=0表示激励信号前沿,将超声波信号P(t)以信号中心为界一分为二,移动信号中心至采样窗口起始处,求得已移动半边信号的相位值ψ(t),则原信号与已移动信号的相位关系为
![]()
式中 θ(f)——信号移动前的相位;
n——某频率信号从t=0至t=td+τ内的周期数。
3.2.3.3 短时傅里叶变换超声衰减谱与相速谱的试验测量
在平均粒径为281 nm、体积浓度为0.4%、温度为10℃的超细氧化锌-水悬浊液中,改变超声信号反射板的位置,获得声程长度分别为40 mm和60 mm的两列超声回波信号,以超声激励信号的上升沿为初始点,将两列超声波信号叠加在一起,最终的波形显示如图3.12所示。
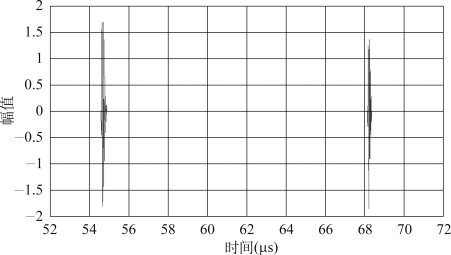
图3.12 超声回波叠加信号
图3.12中,所用信号采样频率为250 MS/s,前列波形的采样起始点为13 500,后列波形的采样终止点为17 100,即68.4μs;前后两列波的长度均为79个采样点,即0.316μs;两列波形之间的声程差为3 380个采样点,即13.52μs。
分别对两信号做快速傅里叶变换,所得频谱信号如图3.13所示。
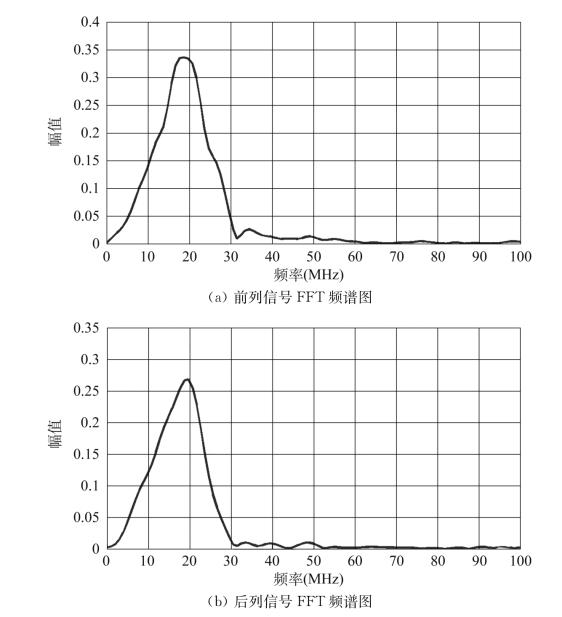
图3.13 前后两列超声回波信号的FFT频谱图
参照式(3.4)、式(3.8)~式(3.10)可分别得到所测氧化锌-水悬浊液中的超声衰减系数及超声相速度。
利用海明窗函数对图3.12的信号做短时傅里叶变换处理,将窗函数宽度定为超声波信号长度的1.5倍,即118.5个采样点,窗函数每移动一个采样点所对应的时间为0.004μs。图3.14为前后两列信号中单一频率20 MHz分量信号的时间-幅值谱图。
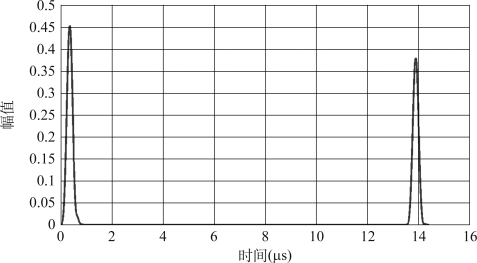
图3.14 20 MHz超声波信号时间-幅值谱图
依次做11~22 MHz单一频率超声信号的时间-幅值谱图,参照式(3.3)、式(3.4)得到所测氧化锌-水悬浊液的超声衰减系数与超声相速度。图3.15、图3.16分别为不同方法所测得的超声衰减谱与相速谱。
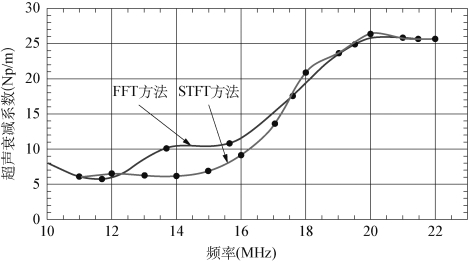
图3.15 氧化锌-水悬浊液超声衰减谱
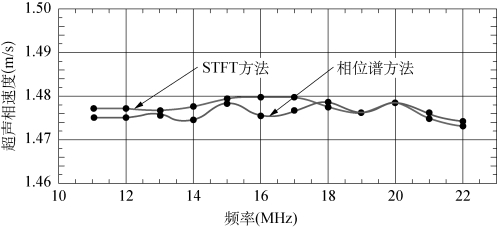
图3.16 氧化锌-水悬浊液超声相速谱
由图3.15,采用短时傅里叶变换所测得纳米氧化锌-水悬浊液超声衰减其总的趋势随频率升高而变大,但是某些频率段的超声衰减系数产生波动,19~21 MHz波动显著增大。分析产生此种现象的可能原因如下:
(1)超声声场自身影响。由于不同频率的单频超声波在相同媒质内传播过程中其声压在声轴线方向的变化规律不同,且声场扩散规律不同,因而产生超声衰减系数波动现象。
(2)测量装置产生的影响。如与超声换能器发射面之间的平行度不是很好以及容器壁面产生的超声反射、衍射造成超声相位损失,也对超声衰减系数的测量产生影响。
(3)所测颗粒两相介质产生的影响。测量过程中,纳米颗粒随时间变化产生凝聚,从而引起超声衰减系数的改变。
短时傅里叶变换测得的结果与快速傅里叶变换测得的结果对比,超声衰减系数变换趋势大体吻合,其中最大超声衰减系数差别在5 Np/m以内,具体的频段范围在12~17 MHz。在该频段范围内,快速傅里叶变换测得的超声衰减系数较小,而快速傅里叶变换方法测得的超声衰减谱在14 MHz附近出现明显跳动,产生这种现象的原因可能是由于快速傅里叶变换的离散化计算使得信号能量分布不均所造成。依据前面章节的分析,当在短时傅里叶变换过程中,增加窗函数宽度,会使得低频信号的分辨率下降,因此通过适当减小海明窗函数宽度,可以减小两种方法所测结果之间的差别。
分析图3.16,对比短时傅里叶变换与相位谱方法分别所测纳米氧化锌-水悬浊液相速谱,相位谱方法所测结果在11~18 MHz频段范围内较短时傅里叶变换所测结果偏小,最大声速差约为5 m/s。分析原因可能是相位谱方法中所测该频段范围内的信号传播声时较长,这可能由于在求解前后两列超声波信号相位差过程中,信号处理系统的信噪比偏低,同时由于低频信号能量较低,导致部分低频信号被淹没在系统噪声中,因此信号偏移时所截取的不是整数周期,造成低频信号偏移距离减小,由此产生相位差变小、声时增加、相速度减小这一现象。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




