固体中的声波特性分析

固体兼具体积弹性和剪切弹性两种性质，其应力、应变和弹性需要用矢量、张量表示，在数学推导方面较为复杂。

假设在无限大弹性固体媒质中一个小体积元δxδyδz，作用在此六面体小体积元各表面上的应力分量为Tij，Tij的下脚标i表示应力的方向，j表示应力所在的垂直于坐标轴的平面。按照牛顿第二定律，该应力分别等于小体积的质量（ρδxδyδz）与各自单一方向上的加速度的乘积，即

式中　ξx、ξy、ξz——质点位移沿X、Y、Z方向的分量。

对各向同性的理想弹性固体媒质，其独立的弹性常数只有拉梅常数λ和μ。其中，μ是剪切模量；λ不对应于弹性力学中的任何弹性模量，但和μ一起，与杨氏模量E、泊松比σ、体积弹性模量B存在以下关系：

利用λ和μ，将广义胡克定律简化为下面形式：

式中　εij——应变的分量；

∆——体积元相对形变，即形变时单位体积的体积增量，∆=εxx+εyy+εzz。

将式（2.20）代入式（2.23），以矢量表示：

或

式（2.25）与式（2.26）即为弹性固体媒质中以质点振荡位移所表示的波动方程。

1）固体中的压缩波(www.xing528.com)

对于固体媒质中的压缩波，可假设ξ为无旋矢量，即

则波动方程为

式中　cl——压缩波的传播速度，。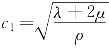

由上，固体媒质中的波动方程与流体中的波动方程相似，当质点仅做X方向振荡时，由于ξy=ξz=0，因此上式可简化为

式（2.28）所表示的即为沿单一方向传播的平面纵波波动方程，表明平面纵波的传播速度就是压缩波的声速。

2）固体中的切变波

与压缩波相对应，假设ξ为螺旋矢量，即

则波动方程变为

式中　ct——切变波的波速，。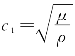

在通常情况下，固体媒质中声波的传播是压缩波和剪切波相互叠加，也就是说可分解成压缩波以波速cl传播，剪切波以波速ct传播。当这两种波在固体媒质中传播时，遇到界面后所表现出来的反射特性，包括反射以及波形的转换等将截然不同。在无损检测中，经常利用该特性得到理想的检测波形用以检查零部件、材料表面或者内部的缺陷。