在小振幅的情况下,将式(2.7)与式(2.8)线性化近似,得到下面的线性方程:
综合式(2.9)~式(2.11),得到以声压p表示的三维波动方程:
式中 ![]() ——拉普拉斯算符,它在不同的坐标系下具有不同的形式。
——拉普拉斯算符,它在不同的坐标系下具有不同的形式。
1)气体和液体中的平面波
对于无限均匀流体媒质中的平面波,在直角坐标系中有
设平面波仅沿X方向传播且为单频简谐波,则其波动方程具有以下形式的解:
关于声压空间部分p(x)的常微分方程为
式中 k——角波数,k=ω/c0,该方程为亥姆霍兹公式。
采用特征值解法,并考虑沿X轴正向传播的平面波,则解为
如果将p(t,x)代入波动方程,则可以得到质点速度为
且有
由此得到平面波的声阻抗率表达式:
综上所述,对于均匀无限的媒质,平面波的波前是无数与声线垂直的无限大的平面,并且传播过程中始终保持为平面。实际上,当平面声源尺寸远远大于声波波长时,即可认为在媒质中所传播的为平面波;当声源为球面或者柱面等其他形式但距离足够远时,如果在其波前上截取小的一块面积,也可以将其波看作平面波。在理想媒质中,如不考虑媒质中的声衰减,则平面波的幅度不随传播距离的改变而发生变化。此外,声压p与质点速度同相,这是平面波所特有的现象。
2)气体和液体中的球面波
对于式(2.12),采用中心对称球坐标系的拉普拉斯算符,有
只考虑简谐波和从坐标原点向外传播的球面波,经过与平面波情况类似的推导,所得波动方程的解为
将式(2.15)代入式(2.7),可求出
式中 pm——声压值,pm=jωρA;(https://www.xing528.com)
um——质点速度幅值,um=![]() ;
;
A——表征振幅的任意参数;
r——波前到圆心的距离。
媒质中如果有球面波传播,其声阻抗率Zs可表示为
其中
式(2.18)表示声阻率,式(2.19)表示声抗率。
3)气体和液体中的柱面波
依据式(2.12),假设有一半径为a的无限长圆柱声源,做柱体径向振荡,在流体媒质中产生柱面波,柱坐标系中的拉普拉斯算符为
只考虑简谐波和外行波,求解波动方程,得到声压表达式为
当kr→∞时,第二类零阶汉克耳函数为
远场声压可简化为
式中 pm——声压幅值,pm= 。
。
相应地,质点速度为
当kr→∞时,第二类一阶汉克耳函数为
远场质点速度简化为
式中 um——质点速度幅值,um=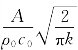 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




