消谐模型在直流电源电压波动下的求解方案

根据上述原理，利用多种群遗传算法对消谐模型进行算法编程，得出三种情况下的开关角度解，如表3-8～表3-10 所示[98]。

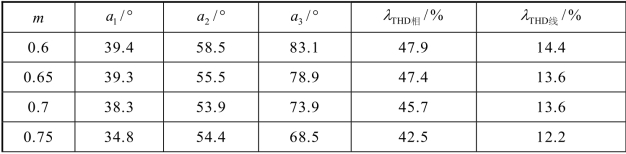
表3-8　情况1：V1＝1 pu，V2＝1 pu，V3＝1 pu

续表

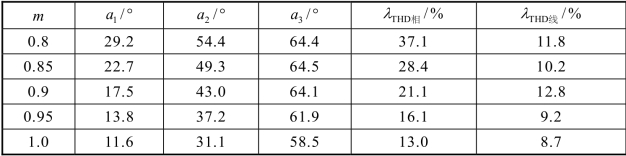
表3-9　情况2：V1＝1 pu，V2＝1 pu，V3＝0.8 pu

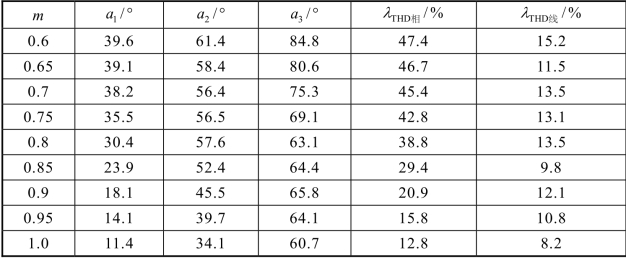
表3-10　情况3：V1＝0.85 pu，V2＝1 pu，V3＝0.75 pu

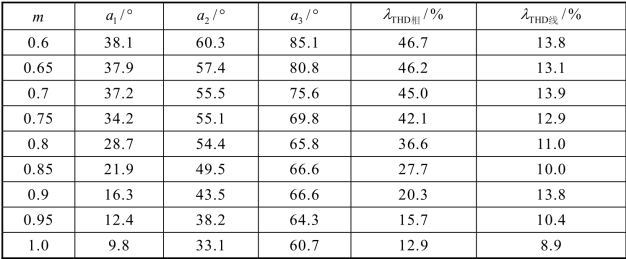
表3-8 至表3-10 分别给出了在不同调制度下，三种直流侧电源在不同情况时满足消谐要求的各开关角度解和对应的逆变器输出相电压和线电压的大小。由各表格中数据可以看出，开关角度和THD 都呈现输出随着调制度的增大而越小的变化规律。开关角度在调制度变化范围内的轨迹如图3-21 所示。

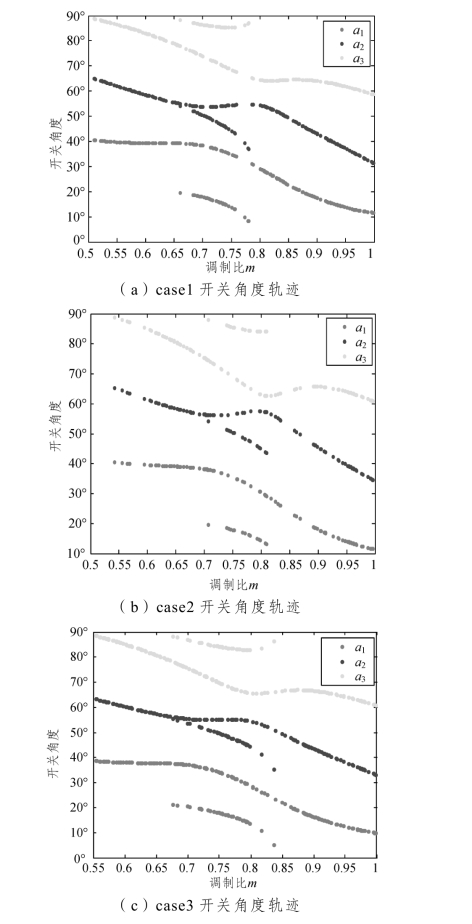
图3-21　开关角度轨迹图

由图3-21 可见，三组开关角度轨迹与传统SHEPWM 角度轨迹一样都具有连续性，且三组开关轨迹都发生了分叉现象，出现两组有效解，这些看似冗余的角度可以增加实际控制时的灵活性。为了对比分叉区间内两组解的差异性，通过计算给出了三种情况下两组解的角度值及输出电压 THD 值，如表3-11～表3-13 所示。(www.xing528.com)

表3-11　情况1：V1＝1 pu，V2＝1 pu，V3＝1 pu 时两组解

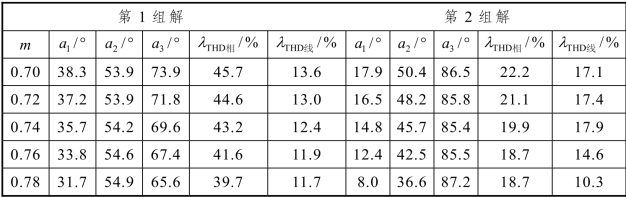
表3-12　情况2：V1＝1 pu，V2＝1 pu，V3＝0.8 pu 时两组解

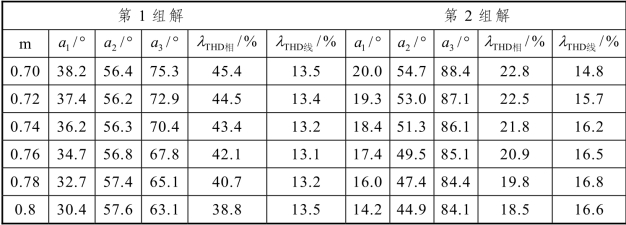
表3-13　情况3：V1＝0.85 pu，V2＝1 pu，V3＝0.75 pu 时两组解

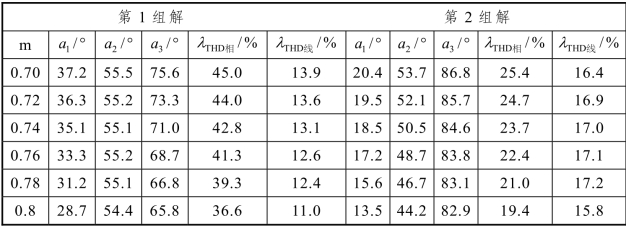
对比表3-11 至表3-13 中数据可见，第1 组解和第2 组解的线电压THD相差不大，但是在相同调制度情况下，第2 组解相电压THD 比第1 组解减小了近50%。在实际控制过程中可以考虑在特定调制区域内选用第2 组解进行控制，以达到最优的消谐效果。为了更加形象地展现输出电压 THD 的变化情况，图3-22 和图3-23 给出了利用Matlab 软件绘制的CHB 逆变器输出电压THD 三维图。

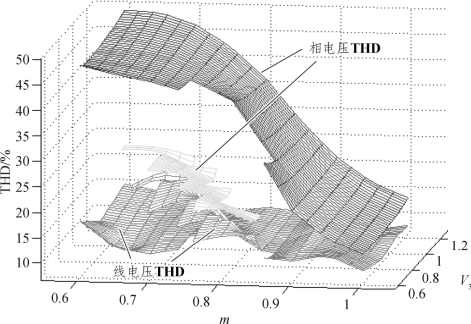
图3-22　V3和m 变化时THD 三维图（V1＝V2＝1 pu）

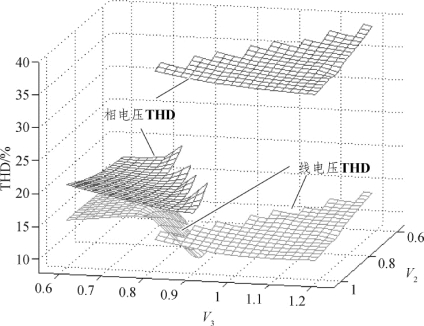
图3-23　V2和V3变化时的THD 三维图（m＝0.8，V1＝1 pu）

由图3-22 和图3-23 可见，CHB 逆变器输出相电压和线电压随调制度变化的规律跟理论计算规律相同，在特定调制度区域，第2 组解和第1 组解线电压THD 值基本接近，但相电压THD 值明显要小很多。