目标函数值与进化代数的关系

选取表3-7 中的5 组数据，利用Matlab 软件绘制出了目标函数与迭代次数的进化过程图，更加直观地反映出两种算法的优化效果，如图3-15 所示。

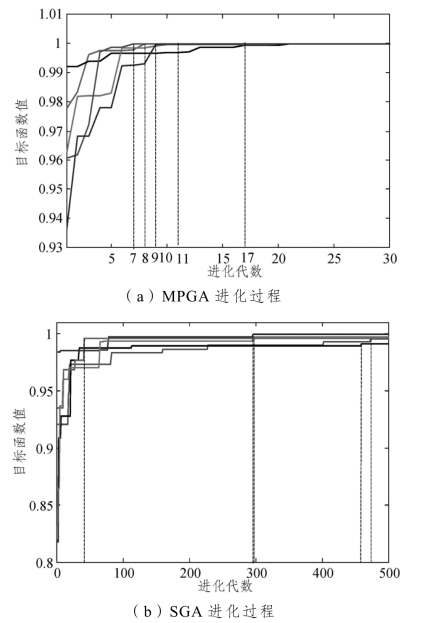
图3-15　目标函数值与进化代数的关系

由图3-15 可见，MPGA 在进化到20 代时已搜索出全局最优解，进化过程目标性非常强；而SGA 的最大进化代数间差距较大，最小和最大代数分别为40 和480 代，进化过程随机性很强。MPGA 在5 次运行中大多能够使得最终目标函数值达到1，优化效果比较精确；而SGA 在5 次运行中目标函数只有一次优化到1，其他各次均不到1，而且还各不相同，存在一定误差。由仿真结果可见，MPGA 算法对目标函数的优化效果更好。

为了对不对称CHB 多电平逆变器多波段SHEPWM 在全调制度范围内的消谐效果进行研究，本节利用MPGA 算法对多波段SHEPWM 消谐模型进行了求解，得出了三个波段下的开关角度轨迹，如图3-16 所示。

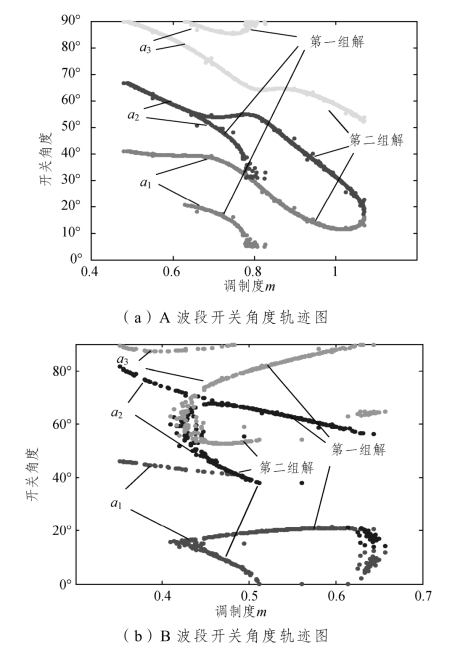
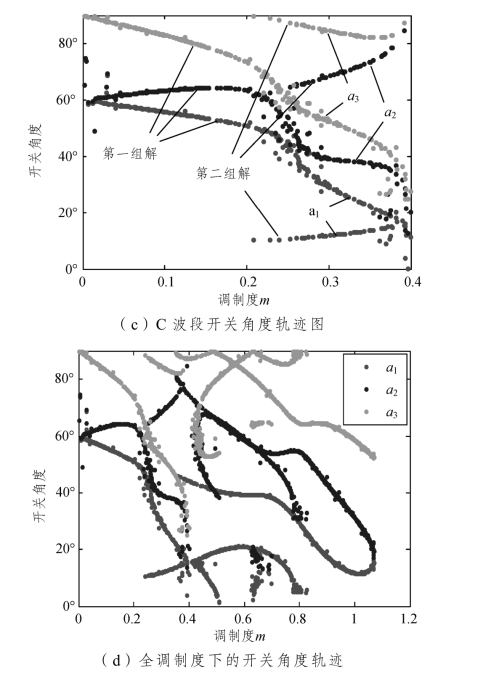
图3-16　开关角度轨迹

从图3-16（a）～（c）中可以看出，三个波段下的开关角度轨迹都有很好的连续性和规律性，这有利于SHEPWM 的在线查表控制。由图3-16（d）可见，A 波段、B 波段和C 波段开关角度解的范围分别介于[0，0.4]、[0.35，0.67]和[0.47，1.10]，基本上覆盖了全部调制度范围，且三个波段的开关角度解在临界区域存在重叠现象，具有一些冗余的开关角度解。另外，三个波段内还存在开关角度多解分岔现象，这增加了在消谐过程中开关角度选择的灵活性。(www.xing528.com)

为了验证开关角度解的正确性，本节进行了建模仿真研究，仿真参数为：A 波段[m＝0.9，16.9°，42.2°，63.9°]、B 波段[m＝0.4，43.9°，73.8°，87.4°]、C 波段[m＝0.12，55.1°，63.8°，81.7°]。A、B、C 波段下CHB 逆变器输出电压波形和频谱如图3-17（a）～（f）所示。

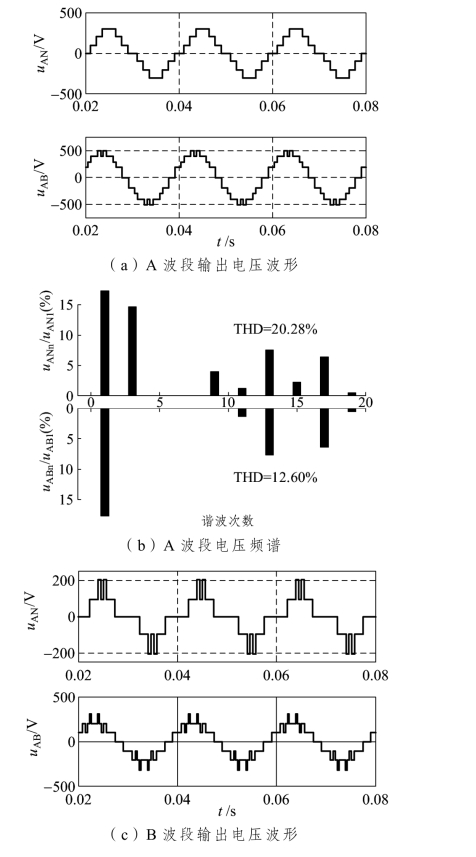
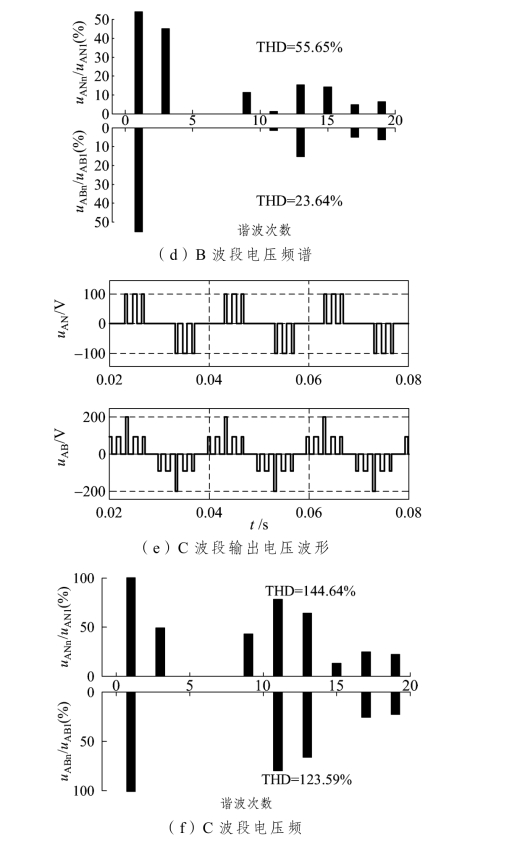
图3-17　电压仿真波形及频谱

由图3-17 可见，CHB 逆变器输出电压中的5 次和7 次谐波均已被消除，且随着调制度的降低，相电压的电平数逐步下降，THD 含量相应上升。为了验证多解的合理性，分别选取A、B、C 波段内的两组不同解进行FFT 分析，得出其相电压THD 变化曲线，如图3-18 所示。

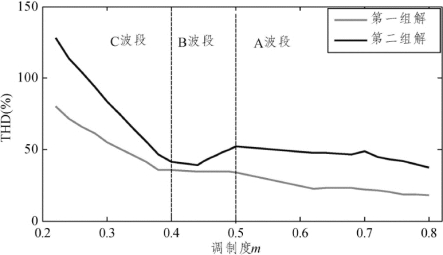
图3-18　THD 值与调制度关系

由图3-18 可见，两组解的值在各波段都有所差异，第一组解控制下逆变器相电压 THD 在全调制度范围内都小于第二组解，因此消谐效果要好于第二组解。但是第二组解作为另一组参考解也能够消除5 次和7 次谐波。