遗传算法及其改进方法

标准遗传算法SGA 是以达尔文自然进化论和自然遗传学为基本思想，是一种迭代自适应及概率性搜索的智能算法。该算法首先需要定义一个解空间，通过适者生存的规则，适应能力大的个体（利于优化目标函数的个体）更容易被选择。然后经过个体随机交叉和变异等操作产生新的个体，使新的种群逐步趋于最优，最后筛选出目标最优个体。SGA 控制主要有种群初始化、选择操作、交叉操作和变异操作等环节。SGA 的主要流程如图3-13 所示。

图3-13　标准遗传算法流程图

早熟是SGA 中较为普遍的现象，主要表现在种群中的所有个体都趋于同一状态而停止进化，从而导致算法得不到最优解。早熟发生的主要原因有：

（1）当种群中存在个别超常个体时（适应度很高），该个体在选择操作中会被多次选中，从而造成下一代种群中所含比例过大，使得群体失去竞争性。

（2）交叉概率 Pc和变异概率 Pm的选取适当与否决定了算法全局搜索和局部搜索能力的均衡，因此进化搜索的结果对 Pc、 Pm的取值非常敏感。

（3）种群规模对算法性能也有较大影响。当种群规模较小时，种群的多样性低，个体间竞争性弱；当规模较大时，会增加计算量，迭代速度较慢。

（4）SGA 常用的终止判据为设定最大进化代数，这样容易造成迭代次数过少而进化不完全的问题。

针对以上的问题，本节提出了 MPGA（Multiple Population Genetic Algorithm，多种群遗传算法），通过引入多个种群同时进行优化搜索，让不同的种群赋以不同的控制参数，实现不同的搜索目标，从而较好地解决了SGA 中的早熟现象[96]。MPGA 算法流程如图3-14 所示。

(www.xing528.com)

图3-14　多种群遗传算法流程图

相比SGA 而言，MPGA 加入了移民算子（Immigrant）、精华种群（Elite Population）和人工选择环节；为了扩大种群的多样性和增大搜索空间而设置多个种群，每个种群中的个体随机产生；为了平衡算法中全局搜索和局部搜索的比重，设计交叉概率cP 和变异概率mP 随着进化代数Gen 的变化而变化。MPGA 通过多个不同控制参数种群的协同进化，同时兼顾了全局和局部搜索，扩大了个体的多样性与竞争性。交叉概率和变异概率与进化代数关系如下：

移民算子的设定方式是将各种群在进化过程中出现的最优个体定期地（每隔一定的进化代数）引入到目标种群之中，替换掉目标种群中的最劣个体，这样就实现了种群之间的信息交换。精华种群（保存每一代每个种群中最优个体）的设定方式是通过人工选择筛选出每一代中各个种群的最优个体，再与上一代精华种群中相应的个体进行比较，如果优于前者则进行替换和保存成为新的精华个体。精华种群的优势在于它不进行选择、交叉、变异等遗传操作，保证了进化过程中各个种群产生的最优个体不会被破坏和丢失。

另外，相对于传统的以进化次数为判据的SGA，MPGA 采用精华种群中最优个体最大保持代数maxGen 作为终止判据，该方法充分利用了SGA 在进化过程中的知识累积，避免了进化次数不够而造成的早熟现象。

本节采用MPGA 对SHEPWM 消谐模型进行求解，本质上属于SGA 的多目标优化问题，因此可以把目标方程组转化为如下的多项式组[96]：

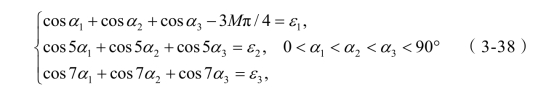
优化目标函数为：

同理可以建立B 波段和C 波段的多项式组。当目标函数优化到最大值1时就等同于SHEPWM 方程组已完成求解。