深入探讨Walsh函数及其变换

1. Walsh 函数原理

Walsh 函数可表示为Wal（n，t），三电平归一化后的1/4 周期波形如图3-5 所示，记c 为1θ 归一化后的开关角度值，把T(0～1)划分为2m个区间，上升沿所在的区间数计为N，图3-5 的波形经Walsh 变换后可得一组Walsh 函数的集合，如下所示：

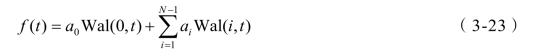
式中：

式（3-23）根据1/4 周期对称性简化如下：

记W4i-3= Fω(4i - 3)为Walsh 变换函数Wal(4i -3， t)对应波形f(t)的Walsh 变换系数，结合图3-5 有：

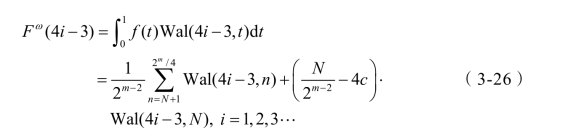
图3-5　归一化波形

2. Walsh 域和傅立叶域的转换

由公式（3-23）可将傅立叶域下的非线性方程组转换为Walsh 域下的分段线性方程组，公式如下：

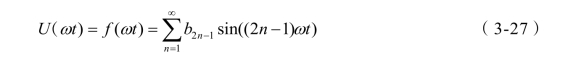
式中：(www.xing528.com)

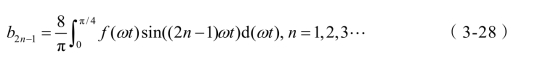
令ω 相等，将式（3-25）式展开至无穷项，使得其与式（3-27）相等，而后将式（3-25）带入式（3-28），整理得：

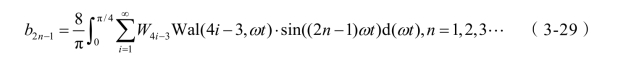
令

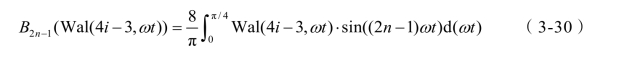
式（3-30）为Walsh 函数Wal(4i -3，ω t)的（2n-1）次谐波的傅立叶系数，将它代入（3-29）式整理可得：

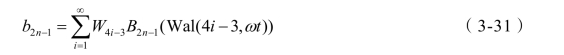
式（3-30）很难求解，文献[80]给出了一种非递归通用公式，令k＝2i-1，i＝1， 2， 3…，m＝4n-3，n＝1， 2， 3…，则：

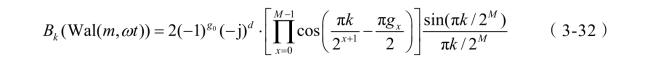
式中，j = ( -1)1/2；m 为Walsh 函数的阶；b 为m 的二进制表达式；记b 的格雷码形式为g，格雷码的第x 位为gx；M 是g 的总位数，d 为g 中1 的个数。

3. 计算步骤

整理（3-30）式得：

式中，[b]和[U]都为谐波系数矩阵；[B]为Walsh 转换矩阵；[F]为Walsh 系数矩阵。令k 次谐波的系数Un为0 即可建立Walsh 变换后的分段线性方程模型，步骤如下：

选定区间总数N，给一组开关角度初值，并利用所计算的归一化后判定区间数作为初始条件；利用式（3-32）计算出转换矩阵[B]；再利用式（3-26）计算系数矩阵[F]；最后利用式（3-33）建立分段线性方程组进行求解。