对称CHB逆变器的TPWM调制原理

1. 梯形波调制（T-PWM）信号

图2-31 所示为梯形调制波 us波形，它由幅值为US的三角波 ust经对幅值±UT截取后得出，UC和UT分别为载波与调制波的幅值，所以调制比M =UT/UC。

图2-31　T-PWM 信号波形

假定幅值比MT=US/UC，梯形波幅值UT与三角波幅值US的比值为δ ，则梯形波的三角化率δ 为：

当δ =1 时对应三角波。假定梯形波上顶边宽为2y，则y 和δ 的关系：

由图2-31 可知，梯形波不是连续函数，因此将一个周期内的梯形波分为5 个区域，在每个区域内，我们可以求解出的三角载波与梯形调制信号的相位交点φ 角。

根据文献[78]可知，利用数学复数形式的双重傅立叶基数公式来表示逆变器输出的PWM 线电压为：

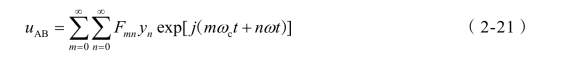
式中， Fmn为复数傅立叶系数，且

则可以计算出复数傅立叶级数 Fmn为：

式中，x=ωct ， y=ωt ， （e x， y） = E·exp[ -j(mx +ny )]。

将计算出的 Fmn值代入式（2-21）中，并将 uAB展开成实数傅立叶级数，得到采用梯形波调制信号的逆变器输出线电压与直流侧电压比值：

式中：

上述为T-PWM 信号输出线电压与直流侧电压比值的关系。因此，把式（2-24）中的相位角 tω 分别滞后2π/3 和4π/3，则可以得到线电压 uAC和 uBC与直流侧电压比的表达式。

2. 梯形波三角化率的选取(www.xing528.com)

IPD-TPWM 策略的原理如图2-32 所示，由于δ 值的选择对CHB 多电平逆变器的直流侧电压利用率跟其谐波特性有着根本性的影响，因此把δ 与两者之间的数学联系进行深刻分析，并根据推导得出的结论选择最优的δ 值。

由式（2-24）可知，基波和n＝3， 5， 7， …次谐波的幅值为

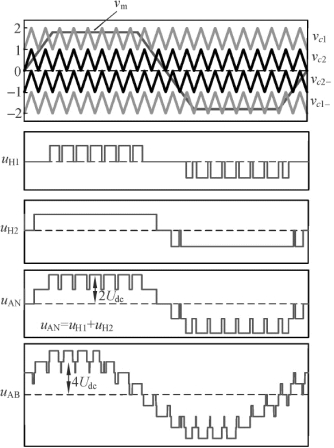
图2-32　IPD-TPWM 策略原理图

由式（2-25）与（2-26）可知：

根据式（2-20），上式中：

将式（2-28）和（2-29）代入式（2-30）可得

由上式可得逆变器输出线电压的总谐波畸变率为

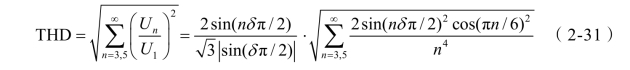
式（2-30）、式（2-31）及式（2-32）分别体现了TPWM 逆变器输出线电压的谐波含量、总谐波畸变率、基波幅值和直流电压利用率。由上述式子可知，谐波含量、总谐波畸变率和基波幅值仅与梯形波三角化率δ 有关，现将Un/U1与δ 、U1，Mi=1(THD )/E 与δ 的关系曲线分别绘制如图 2-33 和图2-34 所示。

图2-33 所示表明了各个低次谐波相对基波的幅值与δ 的关系曲线。由于在输出线电压中3 的倍数次谐波互相抵消，因此不需要进行分析，则该图包含了5 次、7 次、11 次和13 次谐波。当δ =0.4时，虽然7 次谐波含量略高于在0.3≤δ 1≤时的其他7 次谐波含量，但其5 次谐波的含量为0，并且其他的谐波例如11 次，13 次含量很小。

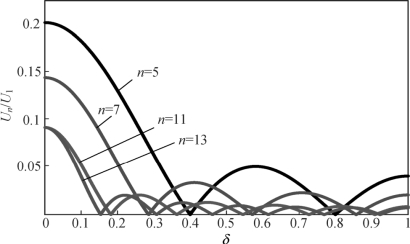
图2-33　各次谐波相对幅值与三角化率δ 的关系

由图2-34 可以得出，当δ 取较小值时，IPD-TPWM 策略的直流电压利用率不仅大幅超过了SPWM 时的0.866，而且打破了1 的限制。随着δ 值由0逐渐向1 处增加， U1，Mi=1/E 逐渐降低，接着梯形波逐渐变成三角波，逆变器的直流电压利用率也随δ 值增加而降低。

图2-34　直流电压利用率及波形畸变系数与三角化率δ 的关系

δ =0.4时，输出基波电压幅值只是略小于δ ≤ 0.4时的基波电压幅值，并且此时得到的线电压总谐波畸变率只稍微高于在δ =0.8附近的谐波畸变率；但δ =0.8时，逆变器输出基波电压幅值却又非常小。因此，综合考虑上述三者与δ 的关系，可以确定δ =0.4时的梯形波为最佳梯形调制波。