特定谐波消除SHEPWM技术优化

特定谐波消除脉宽调制（SHEPWM）法能够以较低的开关频率得到较高质量的输出电压波形，考虑到多电平逆变器通常应用在中高压大功率场合，为了减少器件开关损耗，提高系统效率，通常多电平逆变器SHEPWM 的工作频率限制在1 kHz 左右，因此其数学模型多采用梯形波SHEPWM 的形式进行控制，如图1-10 所示。

该电压波形可以用傅立叶级数的形式表示。由于相电压波形的半波对称性和1/4 对称性，电压波形的基波以及各次谐波可以由下面的公式表示：

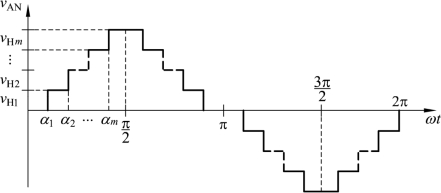
图1-10　2m＋1 电平逆变器的输出电压波形(www.xing528.com)

根据式（1-1），在消除一定数量的谐波时，所有的开关角度必须小于π/2。如果开关角度不满足这个要求，那么该策略就将无法实现。可见传统基于阶梯波的多电平逆变器SHEPWM 控制都只有很窄的调制度范围，这也正是传统基于阶梯波的多电平逆变器SHEPWM 技术在实际应用中的主要劣势。

消谐的建立及求解是多电平逆变器SHEPWM 控制技术中的两个最为核心的问题。按照逆变器输出相电压波形对称性的不同可以把SHEPWM 分为1/4 周期对称 SHEPWM、1/24 周期对称 SHEPWM 和一个周期都不对称SHEPWM 三种。其中1/4 周期对称SHEPWM 消谐的建立和求解最简单，但是要求1/4 周期对称也限制了解的空间。针对1/4 周期对称SHEPWM 消谐模型数值算法求解的方法主要有牛顿法[31]、同伦法[32]、多项式合成法[33]和Walsh 函数变换法[34]几种。其中牛顿法对开关角度初值的依赖程度很高，如果找不到与准确值较为接近的初值则有可能导致迭代算法不收敛；同伦法的收敛速度快，对初值的依赖程度较小；多项式合成法是将消谐模型转化为多项式方程组进行求解，该方法需要根据不同电平数SHEPWM 进行多项式的重新推导，不利于推广应用；基于Walsh 函数变换法是利用Walsh 函数对该数学模型进行变换，把对非线性方程组求解的难题转换为对分段线性方程组的求解问题。该方法使得对多电平逆变器SHEPWM 的开关角度实施在线计算及实时控制成为可能。

上述研究文献都是对相电压波形满足1/4 周期对称SHEPWM 进行的研究，但是1/4 周期对称并非是必须的约束条件。如果取消1/4 周期对称的约束条件也可以进行 SHEPWM 控制，而且取消 1/4 周期对称约束后可以使SHEPWM 消谐模型具有无穷多组解[35]。文献[36]对一个周期内无对称两电平SHEPWM 和五电平SHEPWM 进行了研究，该方法SHEPWM 变量多，所建立的消谐模型比较复杂，因此几乎没有什么实用价值。

文献[37，38]比较了1/4 周期对称SHEPWM 和1/2 周期对称SHEPWM开关角度解的区别与联系，指出1/2 周期对称SHEPWM 可以得到无穷多组满足消谐要求的开关角度解，并给出了两种类型的数值解。这些文献都只从某一个方面对1/2 周期对称SHEPWM 进行了相关研究，尤其是在对所建立的半周期对称SHEPWM 非线性方程组进行算法求解方面，上述文献都是利用了Matlab 软件下提供的一个 fsolve()函数来进行求解的。但是该函数对初值的精确度要求较高，而求解所得到的开关角度的精度却不高，当初值不够精确时，fsolve()函数还会发散不收敛，无法求解出所要的结果。

除了上述SHEPWM 控制方法以外，文献[39-43]还对遗传算法[39]、蜂群算法[40]、粒子群算法[41]、改进遗传算法[42，43]等智能算法求解SHEPWM 消谐模型进行了研究，这些优化算法都是仿生优化算法，具有自学习、自训练和自优化的能力。如何将这些方法应用到多电平逆变器SHEPWM 控制中，与传统的多电平逆变器SHEPWM 控制方法相结合，将会是非常具有理论意义和研究价值的新思路和新方向。