应用示例：声衰减在3.5中的作用

在多晶金属中，一个晶粒本身就是弹性各向异性的。一个晶粒的晶轴与相邻晶粒的晶轴取向可以不同，各个晶粒在密度上也可能有所不同（双相合金就是一例），在晶界上也可有析出物。这样，当晶粒尺寸D不是远大于入射声波的波长λ时，这种声特性的不连续性可使晶粒产生几乎各向均匀的再发射声波，称为散射波，由之而引起的入射声压的下降为散射衰减。这是在金属中引起声衰减的主要因素。

利用声衰减来表征材质的差异或变化，衰减系数的绝对值有时并不特别重要，往往重要的是其相对变化，试举例如下。

1.微观组织差异的频谱表征

不同的微观组织所引起的声衰减可不同。图10.3-22a、10.3-22b所示为Ti-6A1-4V合金试样A和试样B的宏观组织和微观组织。用带延迟段的10MHz接触式宽带直射纵波平探头进行试验，用时间选通门取出试样A和B的前表面和背面反射信号进行频谱分析，结果如图10.3-22c所示。可以看出，两试样尺寸相同，前表面反射信号的频谱是几乎相同的而背面反射信号频谱则相差甚大。对于粗大的微观组织（B），背反射信号的幅度及频带宽度较之细晶组织（A）要低得多、窄得多。

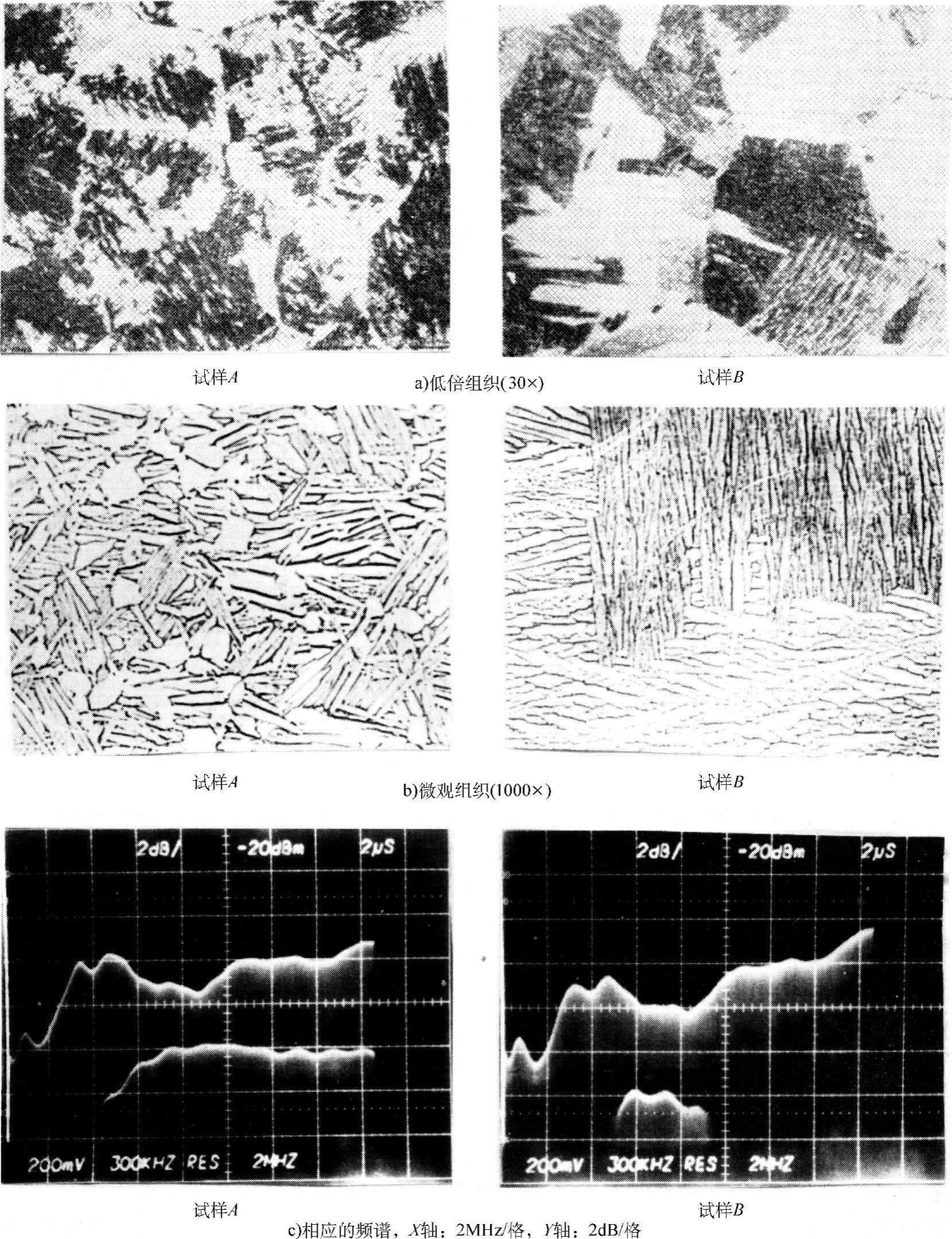
图10.3-22 Ti-6A1-4V合金试样A和试样B的比较

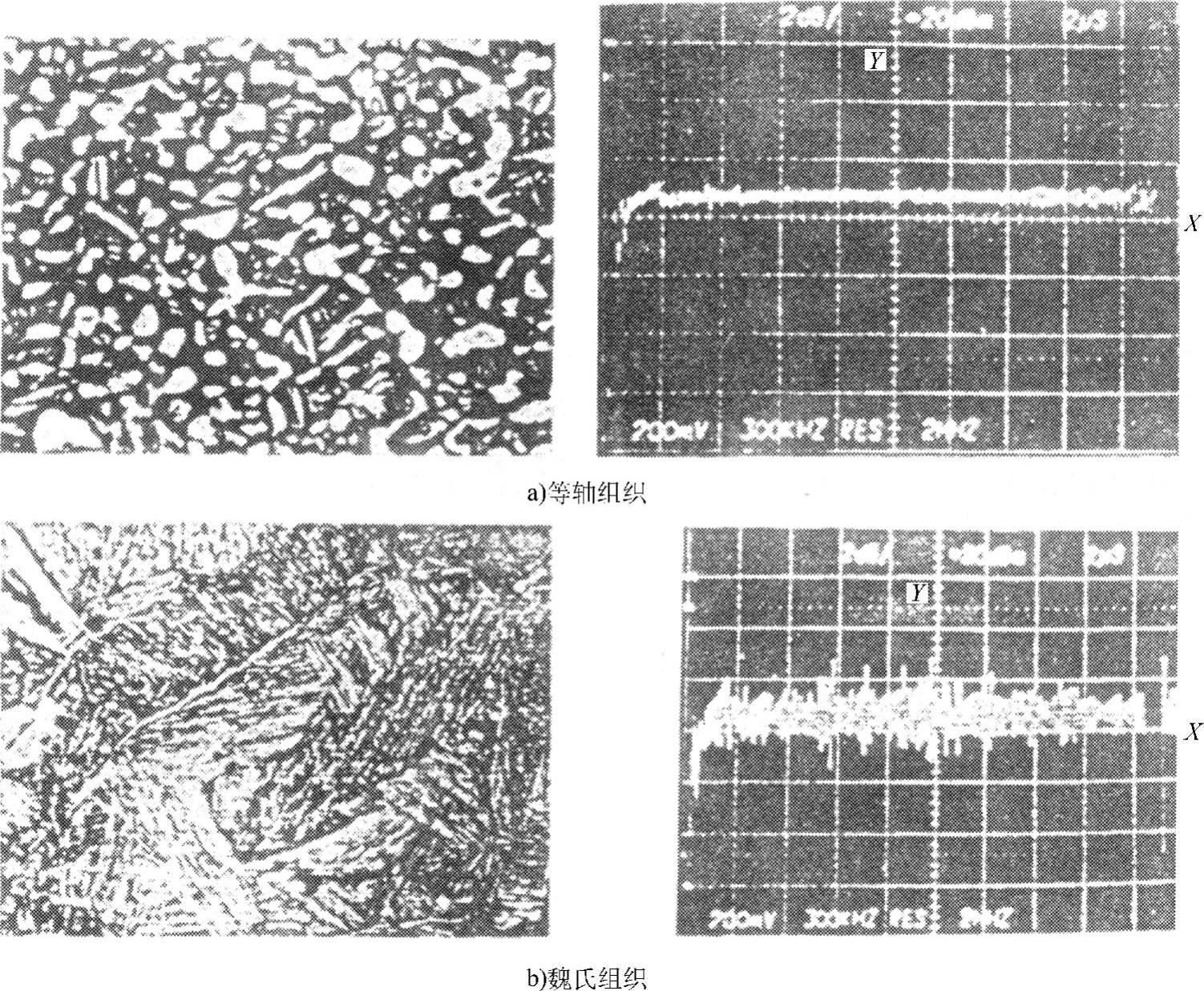
图10.3-23 两种不同组织的Ti-6A1-3Mo-Zr-Si 合金锻坯微观组织的超声波反向散射表征

X轴：3μs/格Y轴：200mV/格

2.微观组织差异的反向散射表征

对于上、下表面并不平行的试样，微观组织的差异在一些情况下，可用以杂波形式出现的反向散射波来表征。图10.3-23所示为两种不同组织的Ti-6A1-3Mo-Zr-Si合金锻坯微观组织的超声波反向散射表征，差异是相当明显的。

3.多晶固体断裂韧度的表征

断裂韧度是一个非本征的外赋力学性能，测量的是材料的断裂抗力。在此应力强度下，裂纹将变成不稳定的，可作灾难性的长大。已经知道，在多晶固体中，断裂韧度是受微观组织和形态控制的，因为超声波衰减也受类似因素控制，所以两者之间有一定的关系。图10.3-24和图10.3-25是说明不同微观组织下，韧度与超声波衰减因子关系的两个例子。从图10.3-24可以推出晶粒尺寸的减小与韧度的增大相对应的结论；图10.3-25的显微照片则说明了相反的情况，晶粒（碳化钨晶体）尺寸的增大与韧度的增大相对应。但是，这种与晶粒尺寸的视在关系是易于使人误解的，因为实际上控制断裂韧度的是带有高位错密度的钴结合剂的体积。显然，与晶粒尺寸乃至晶粒的形状和纵横尺寸相比，要更多考虑控制断裂的标志因素。超声波检测补充了在显微照片上所看到的信息，可以使我们增加对控制动态断裂行为因素的了解。

分析表明，除了晶粒尺寸和形状外，能量在晶粒边界的反射和弹性散射、弹性各向异性和位错阻尼都是构成断裂韧度和超声波衰减的因素。超声波衰减可以预示金属中活性裂纹附近出现的裂纹钝化区尺寸（特征长度），如图10.3-26所示。图中，横坐标刻度为（K_IC/σ_y）²，纵坐标刻度为C_lβσ。这里，C_l为超声纵波速度，为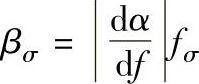，表示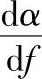是在频率f_σ=C_l/σ时评定的，而σ为与平均晶粒尺寸相当的超声波波长。裂纹钝化区范围越大，局部吸收能量就越多，断裂韧度也就较大，这就形成了用超声波法将金属按断裂韧度分等的基础。

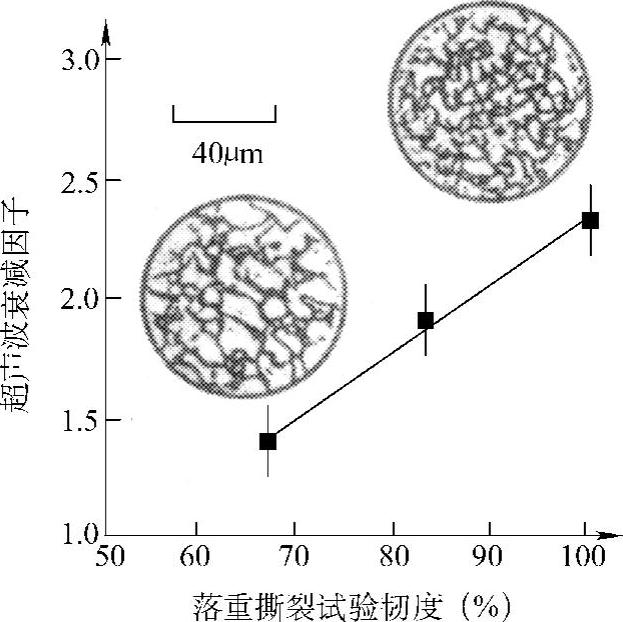
图10.3-24 对于低碳钢落重试验，所测得的韧度与超声波衰减因子的关系(www.xing528.com)

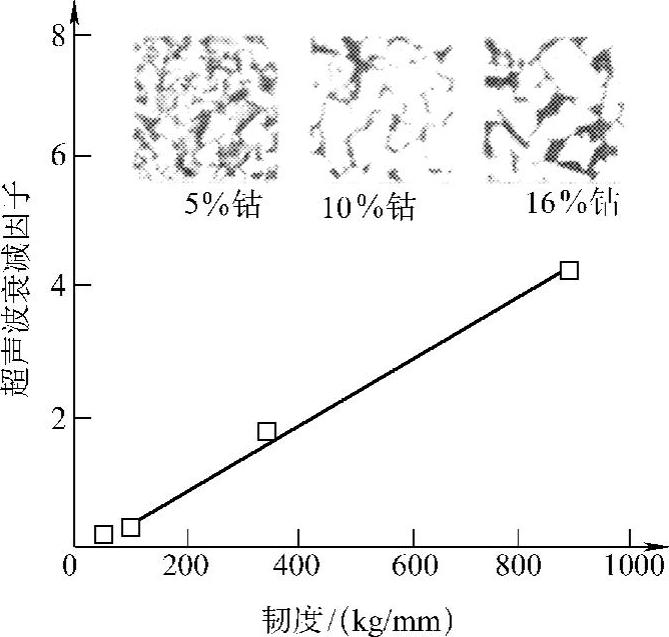
图10.3-25 用Palmovist法测得的碳化钨-钴（WC-Co）合金韧度与超声波衰减因子的关系

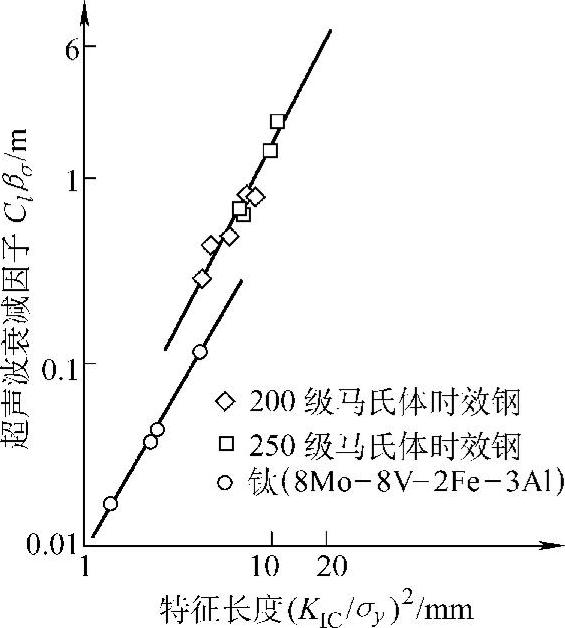
图10.3-26 超声波衰减因子与断裂韧度因子（特征长度）的关系

4.多晶Ti合金微观组织的表征

利用在时间域中第一个背面回波具有多于1个峰的换能器，这前两个峰值之比用作一新的超声波参数，称之为时间域峰值比。已经发现，这回波在时间域的峰值比与其在自功率谱中的两峰值比有线性关系，这表明时间域峰值比可用来研究频率与衰减的关系。与通常的衰减参数相比，这参数的优点是需对第一个底面回波进行分析，也仅需在时间域进行，且与耦合情况无关。由于只需要第一个背面回波，对于有相当高衰减、难以获得好信噪比、多次背面回波的大厚度材料来说是有用的。时间域峰值比与耦合情况无关，有重要的实用意义，就是说如果时间域峰值比用于微观组织的表征，对于在线检测，则由于耦合情况的变化所引入的测量误差可减至最小。作为示例，图10.3-27和图10.3-28为在不同固溶温度下的VT14钛合金（Ti-4.5Al-3Mo-1V）上所进行的工作。

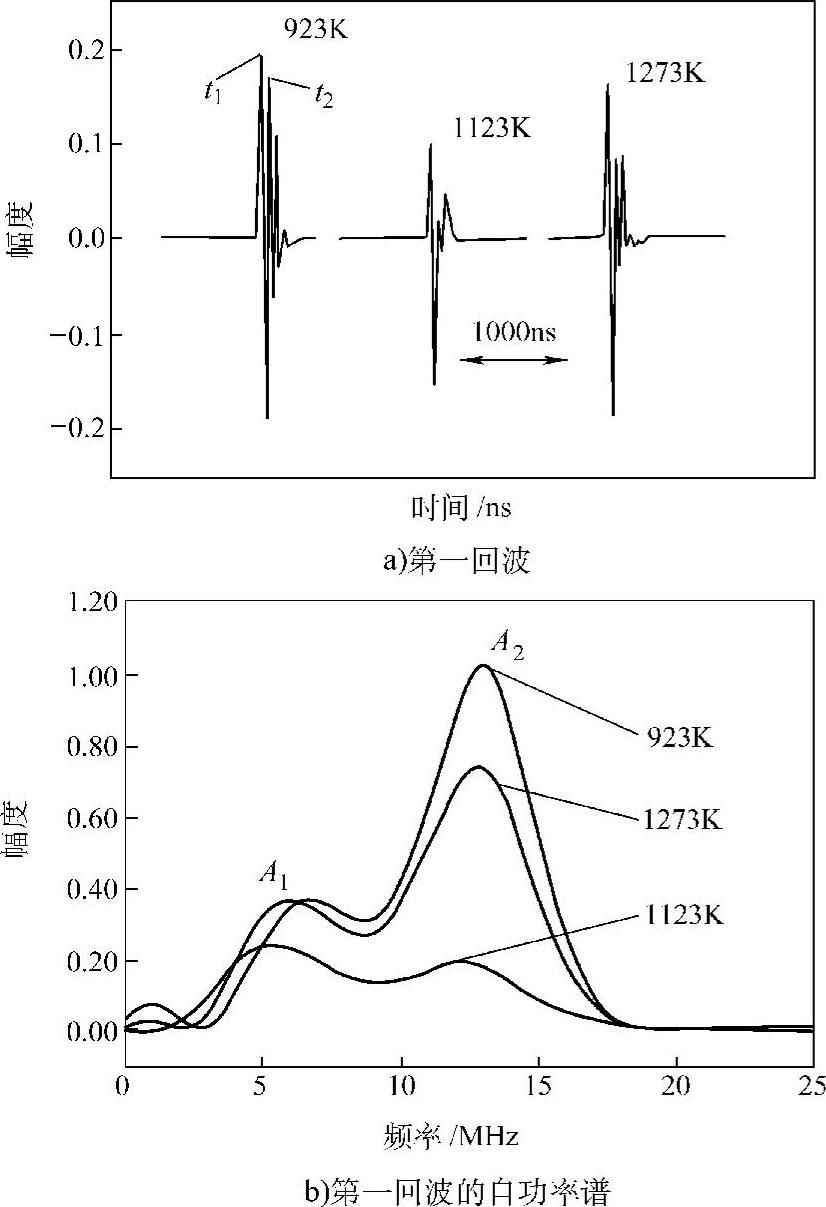
图10.3-27 背面回波（幅度单位任选）试样在923K、1123K和1273K（1202℉、1562℉和1742℉）的热处理1h后水淬

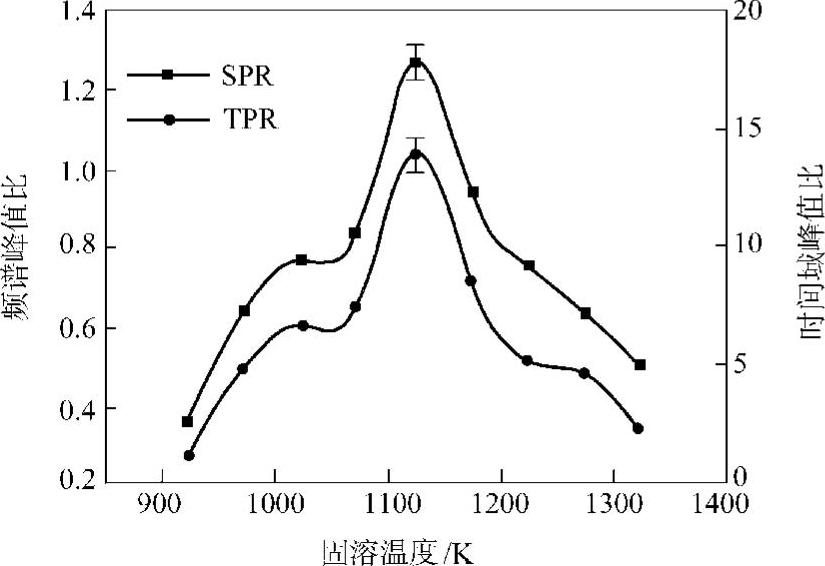
图10.3-28 不同的固溶退火温度频谱峰值比和时间域峰值比（TRR）的变化

5.钢中珠光体层间间距的测定

超声波能量的衰减取决于材料组织的变化，珠光体层之间的晶粒尺寸和层间距离大都会影响钢中超声回波的特性。在晶粒尺寸不变的情况下，衰减随层间距离的增大而上升。

为了确定珠光体的层间距离，可采用超声脉冲回波法。当试样和探头间的耦合保持良好不变时，超声波的衰减可从一次和二次底波的幅度差来测得。相关因子φ（d/l₀）可用来修正底面回波随距离而引起的幅度线性下降。这里，d为试样厚度，l₀为近场长度。平均进给量尺寸B=0.022mm和B=0.177mm珠光体的层间距与衰减系数的关系如图10.3-29所示。

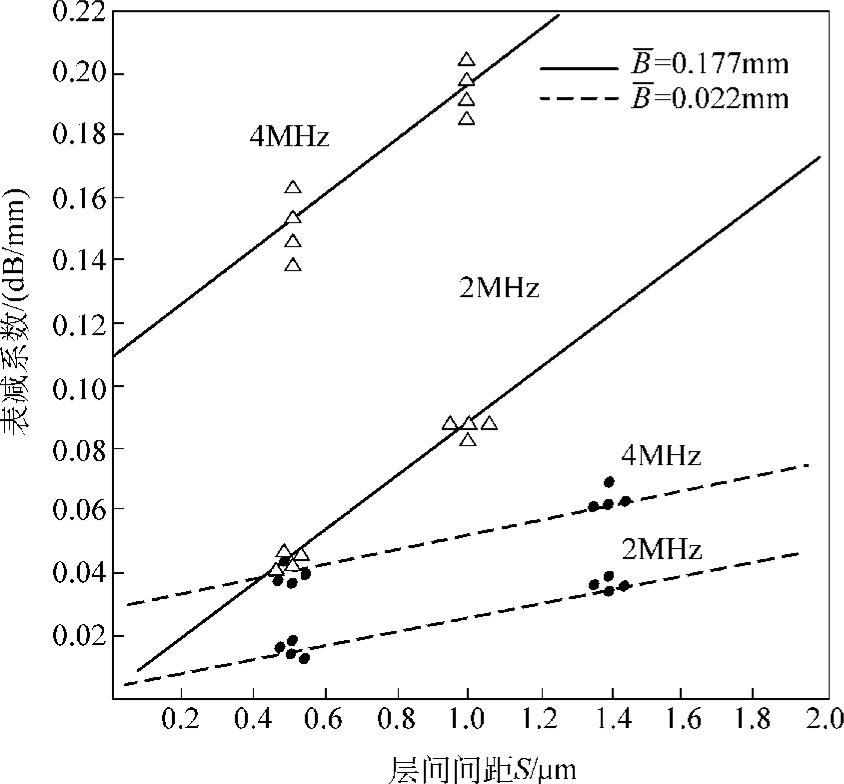
图10.3-29 平均进给量尺寸B=0.022mm和B=0.177mm珠光体层间距与衰减系数的关系