弹性与广义胡克定律的分析介绍

1.弹性

金属的弹性行为起源于其晶体点阵内原子间的相互作用——吸引作用和排斥作用，当两者达到平衡时，金属就处于最低的能量状态。当外力迫使原子靠近或分开时，平衡被破坏，在外力和吸引力、排斥力之间建立起新的平衡，使原子稳定在新的平衡位置上，金属就发生变形。如果此外力还不足以在晶体内部产生其他质的变化，则一旦此外力去除后，由于这种新的平衡又被破坏，为了恢复平衡，原子将重新恢复到原来所在的吸引力和排斥力达到平衡的位置，于是物体在宏观上恢复了原状，这就是弹性变形的物理过程。在变形量较小的范围内，金属弹性变形的应力和应变之间存在着正比直线关系，即所谓的胡克定律。

2.固体中的应变分析

固体发生应变时，不仅各方向的长度可发生变化，同时棱边夹角也会发生变化。前者是长度应变，后者是切应变。从弹性体中取一小体元dv分析与xOy面平行的面的投影面形变，如图10.1-14所示，应变前棱边为M′A′和M′B′，形变后移到M″A″和M″B″。

如取M（x，y，z）点的位移为（ξ，η，ζ），则M′的位移为（ξ，η），由于介质中各点位移不同，（ξ，η，ζ）均为坐标（x、y、z）的函数，所以A′（x+dx，y）沿x轴的位移为（ξ+∂∂ξxdx），线段M′A′沿x轴的伸长相对值为

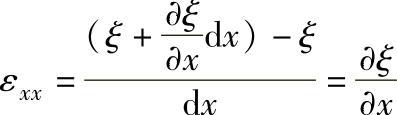
称为x方向的伸长应变。同理可得，y方向和z方向的相对伸长应变为

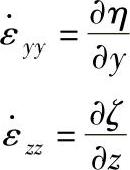
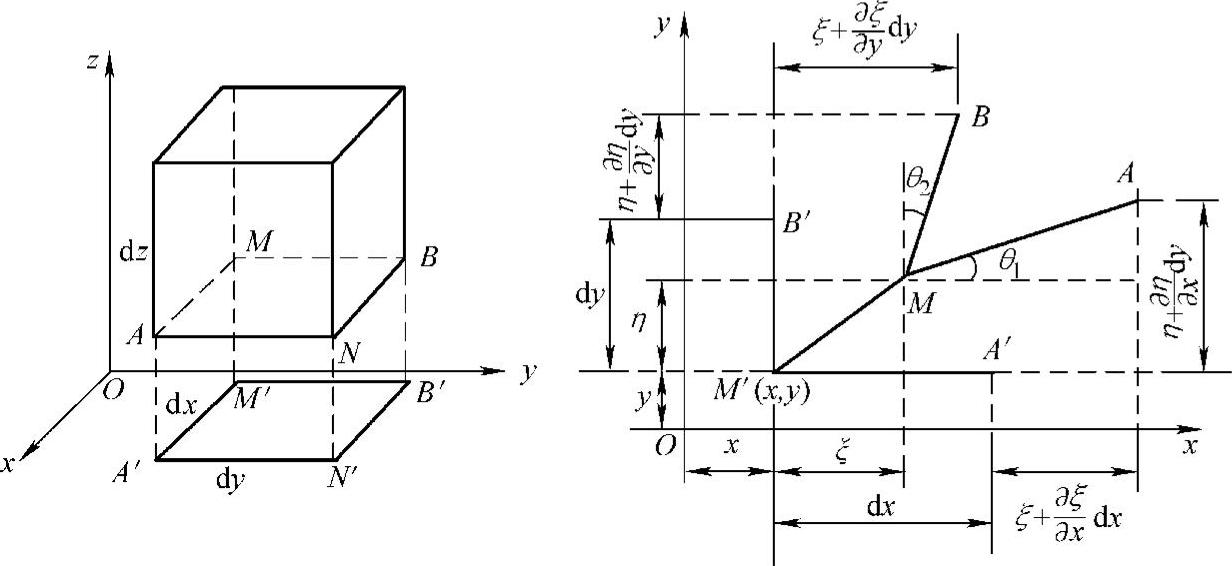
图10.1-14 固体内小体元的应变

∠B′M′A的形变可以用M′A和M′B的交角变化量（θ₁+θ₂）表示，它反映投影面A′M′B′N的切应变。由于M″（x，y）点沿y方向的位移为η，所以A（x+dx，y）的y方向位移为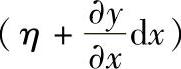，而M″A″的长度变为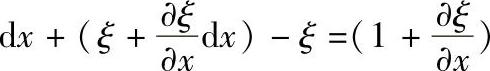dx，所以M″A″相对于M′绕Oz转角

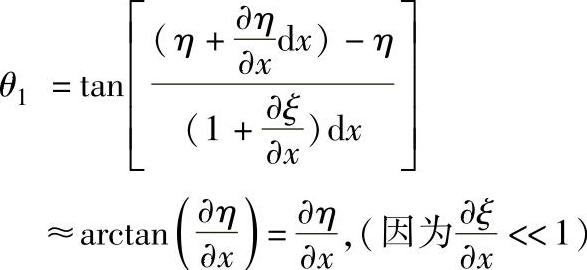
同理可得y方向棱边绕Oz轴的旋转角

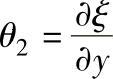
因此，立方体在xOy平面中两棱边的切应变，同理可得：

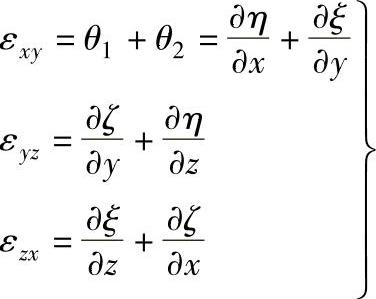
可见，形变分量有六个，即三个伸长应变ε_xx、ε_yy、ε_zz和三个切应变ε_xy、ε_yz、ε_zx。(www.xing528.com)

3.固体中的应力分析

设想从弹性体中取一小体元dv来进行分析，切去部分对dv作用的力作用在断面上，断面上的不同点取同样大小的面积，其上作用力大小不等，方向也不同。同样，在断面上一点附近取一小面积元ds，当所取面积的大小改变时，作用在ds的力f的大小和方向也随之改变。当ds趋于零时，f/ds的极限值定义为该点的应力向量f，其方向等于其极限方向，其大小等于f/ds的极限值。应力向量f在坐标轴上的三个分量f_x、f_y、f_z称为该面的应力分量。可以证明，只要知道通过该点所作的三个相互正交的微分面元上应力向量的分量，就可以确定过该点任意方向面元上的应力分量。三个微分面元上可有九个应力分量，表示为

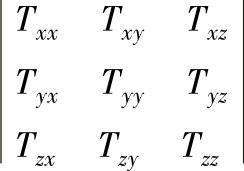
式中，应力分量的下标前一字母表示力所作用的面的法线方向，后一字母表示力的作用方向，如图10.1-15所示。此外，我们用T_ij（i，j=x，y，z）来表示应力，则当i=j时，表示法向应力；当i≠j时，表示切应力。稍加证明还可指出，一般这九个应力分量并不完全独立，它们具有对称性，即T_ij=T_ji，因此实际上，只要用六个应力分量就可完全确定固定的应力特性。

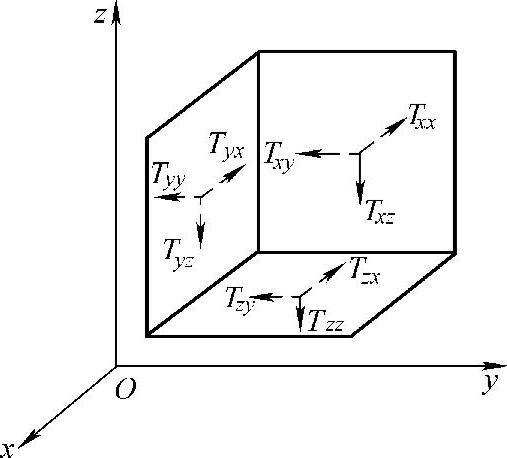
图10.1-15 固体中的应力分量

4.广义胡克（HOOK）定律

假定所研究的是小形变的情况，应变与应力具有线性关系，而且所有的应变分量对每一应力分量都有贡献，所以每一应力应该是六个应变分量的线性函数，它们的一般关系式可表示成以下形式，这就是广义胡克定律。

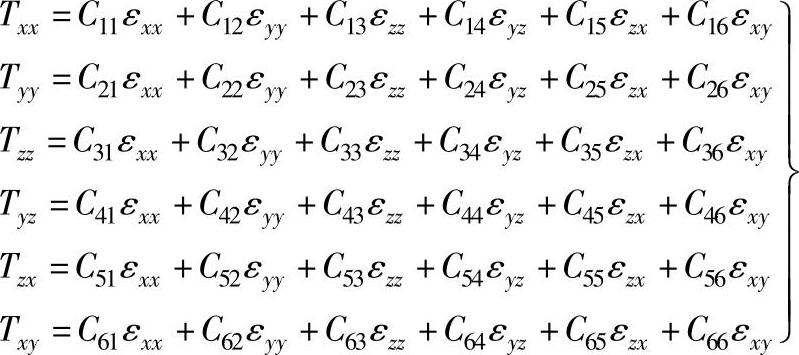
式中，各个系数C_ij（i，j=1，2，3，4，5，6）称为弹性系数（弹性模量），它决定于固体的弹性。由上式可知，这样的弹性模量共有36个，但是实际上这36个系数不是完全独立的，因为弹性模量是应变的单值函数，故可以证明弹性模量具有对称性，即C_ij=C_ji。这样，独立的弹性模量就减少到21个。

工程上用的金属材料一般是多晶体，可认为是伪各向同性的，因此，只有两个弹性模量，即（正）弹性模量（杨氏模量）E和切变模量G，两者关系是

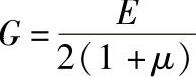
式中，μ为泊松比（μ=ε_xx/ε_yy），表示单向受力状态下横向变形与正向变形间的关系。此外，在各向同性体的金属材料上还有一个体积弹性模量K，它表示物体在三向压缩（流体静压力）下，压强p与体积变化率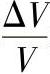之间的线性比例关系

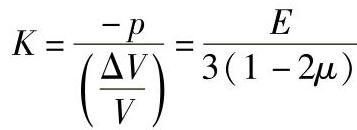
在E、G、μ、K这四个表征多晶体金属材料的弹性性质基本参数中，只有两个独立，即一般把E和G看做是独立的。