如何确定相位差Δ的值？

式（6.3-3）和式（6.3-4）中的Δ是物体变形使P、Q点光程差变化而导致的相对相位差。参考图6.3-4，计算变形前、后由P（x，y，z）点反射至像平面的光波的光程差：

变形前：l=SP+PO，其中：

SP²=（x-x_s）²+（y-y_s）²+（z-z_s）²

PO²=（x-x_o）²+（y-y_o）²+（z-z_o）²

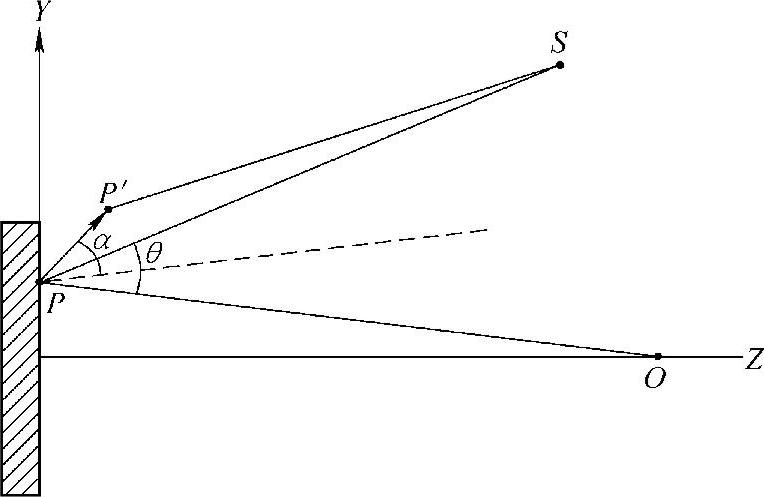
图6.3-4 位移与光程关系

变形后：l′=SP′+P′O，其中：

SP′²=（x+u-x_s）²+（y+v-y_s）²+（z+w-z_s）²

P′O²=（x+u-x_o）²+（y+v-y_o）²+（z+w-z_o）²

略去小量后可得到：

(www.xing528.com)

其中R²_o=x²_o+y²_o+z²_o，R²_s+x²_s+y²_sz²_s。

对于在底片上与P成像于同一点的Q（x+δx，y，z），其位移可表达为（u+δu，v+δv，w+δw），于是与P（x，y）点一样，可得光程差表达式：

所以：

其中：

一般情况下R_s、R_o都较大，故：很小，可以近似认为D=0，而略去。所以有：

此式为错位散斑干涉测量技术的基本关系式。式（6.3-4）与式（6.3-5）建立了ES技术中变形与干涉图像之间的联系。激光全息和ESPI技术得到的干涉条纹图大致可视为等位移图（通常关注离面位移，得到环状条纹图可近似视为等高线图），与之相比，错位散斑得到的干涉条纹图的物理含义复杂，解释更为抽象。