全息干涉测量方法：时间平均法

采用与实时法、双曝光法相同的光路，对作稳态周期振动的物体，用比振动周期大得多的曝光时间进行记录。这样获得的全息图，在参考光束的照射下，物像表面会出现干涉条纹。这些干涉条纹带有物体振幅的信息。这种全息干涉测量方法，称为时间平均法。

从实质来看，时间平均法实际上是多次曝光干涉法的一种极限情况。略去推导过程，时间平均法记录的干涉条纹图光强可表示为

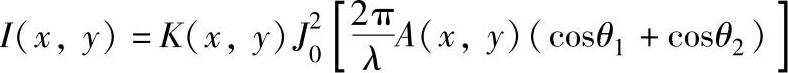
式中 K（x，y）——与位置（x，y）有关的一个常数；

A（x，y）——该点处的振幅；

θ₁，θ₂——振动方向与光源入射方向及干版观察方向之间的夹角（见图6.2-4）；

J₀——0阶贝塞尔函数。

0阶贝塞尔函数J₀的平方的函数曲线见图6.2-6。(www.xing528.com)

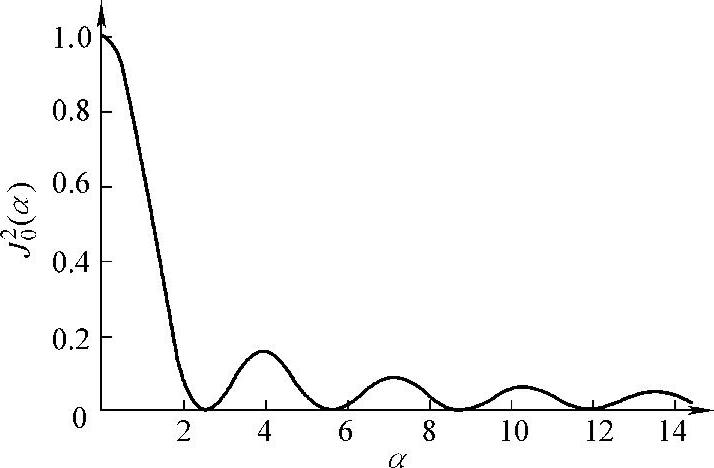
图6.2-60 阶贝塞尔函数平方的曲线

令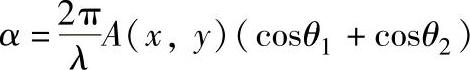。当J₀（α）=0时，I=0，出现黑色的干涉条纹。

设J₀（α）=0的根为α_i，i=1，2，3，…称为条纹级次，那么有：

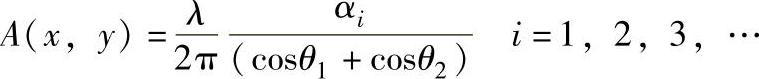
上式表明物体各点的振幅A（x，y）与像上的干涉条纹i之间的定量关系。比较上式与双曝光法的位移计算公式，其型式十分相似。条纹级次反映的是振幅在灵敏度矢量方向上的投影。只是在时间平均法中条纹级次不是按照整数逐级增加。出现亮条纹的前4级亮条纹的位置分别是：α₁=2.40，α₂=5.52，α₃=8.86和α₄=11.79。

从图6.2-6贝塞尔函数平方的曲线可以看到不同条纹级次之间的光强分布规律。位移为零处得到最亮的条纹。所谓位移为零的地方也就是谐振动中的节线。高级次的亮条纹光强衰减得很快，第1、2、3级亮条纹的光强分别只有零级的16%、8.9%和2.3%，这意味着高级次亮条纹的对比度下降，很不清楚。