双曝光法及其应用于固支方板载荷测试的原理和实验结果

图6.2-3为双曝光法的光路示意图。扩束镜L₁、L₂后的SF₁、SF₂为空间滤波器，改善光源质量。快门在物体变形前后分别开启一次使全息干板两次曝光。干板经过显影、定影处理后，用原来的参考光再现。这时物体变形前后的两个物光波同时出现。由于变形引起它们之间的相位改变，从而发生干涉，形成干涉条纹图。利用干涉条纹可测量物体表面位移。

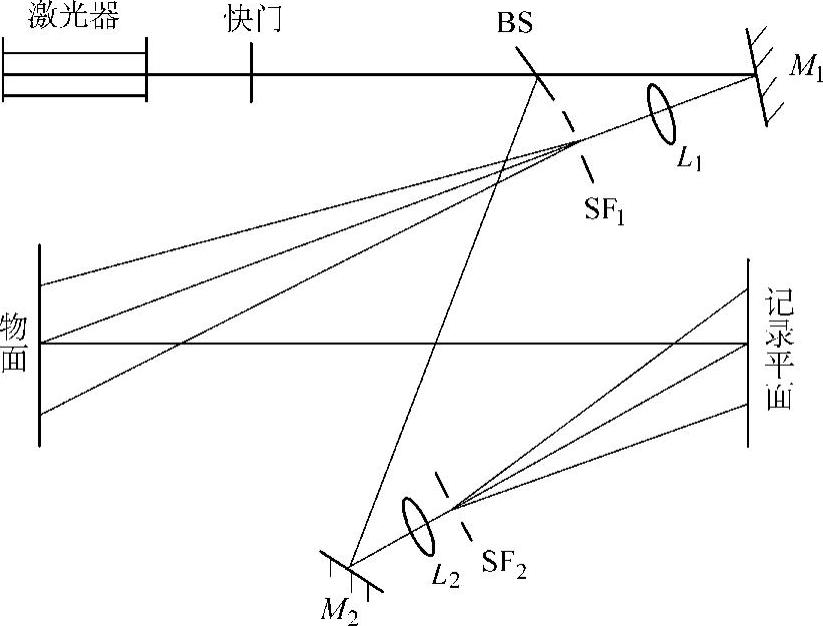
图6.2-3 双曝光法记录光路

双曝光法产生干涉条纹的过程推导如下：

设物体变形前物光波复振幅为O=O₀（x，y）exp[iφ₀（x，y）]

物体变形后物光波复振幅为O′=O₀（x，y）exp[iφ（x，y）]

参考光光波的复振幅为R=R₀（x，y）exp[iφ_r（x，y）]

第一次曝光时到达全息底片的光波是H₁，光强是I₁。

H₁=O+R

I₁=H^∗₁·H₁=（O^∗+R^∗）（O+R）

第二次曝光时到达全息底片的光波是H₂，光强是I₂。

H₂=O′+R

I₂=H^∗₂·H₂=（O′^∗+R^∗）（O′+R）

两次曝光总光强为：I=I₁+I₂=（O^∗+R^∗）（O+R）+（O′^∗+R^∗）（O′+R）

在一定的曝光量范围内，振幅的透射率与光强成正比，为简化起见，取比例常数为1。将两次处理后得到的全息图，用原参考光照明，其透过的物光波ψ为

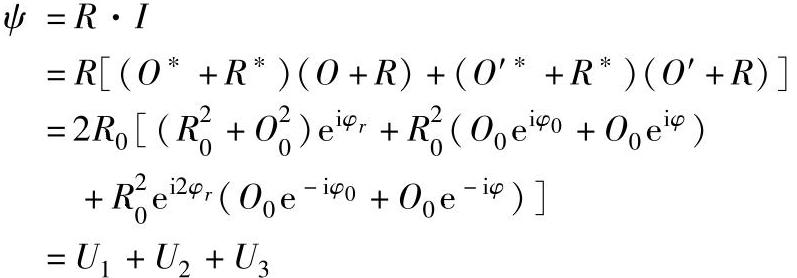
其中第一项U₁是零级衍射波，第二项是两个重现的物光波，一个是变形前的，一个是变形后的，第三项是共轭光波，其中第二项是我们感兴趣的。U₂形成虚像，可透过底片看到，其光强为：

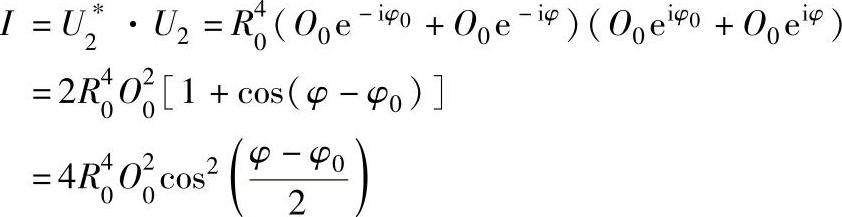(www.xing528.com)

上式表明，两次曝光所得到的虚像的光强是相位差（φ-φ₀）余弦的函数。当φ-φ₀=2mπ（m=0，±1，±2，…，称为亮条纹级数，位移为零的地方为0级条纹）时为亮条纹；当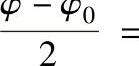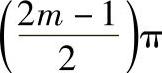（m=0，±1，±2，…，）时出现暗条纹。

位相差与被测物体表面位移量的关系。如图6.2-4所示。设变形前物体表面的点P，变形后产生微小位移d移动到P′。照明光源位置为S，全息底片位置为H，设∠SPH的角平分线为PO，设θ₁=∠SPP′，θ₂=∠HPP′，分别为入射光、反射光与位移方向之间的夹角。

第一次曝光时物光的光程为（SP+PH），第二次曝光时物光的光程为（SP′+P′H）。位移量与物光光程相比是极小量，可以认为变形前后角θ₁和θ₂不变。由于位移d引起的光程差Δ=（SP′+P′H）-（SP+PH）=dcosθ₁+dcosθ₂

相应的相位差为：

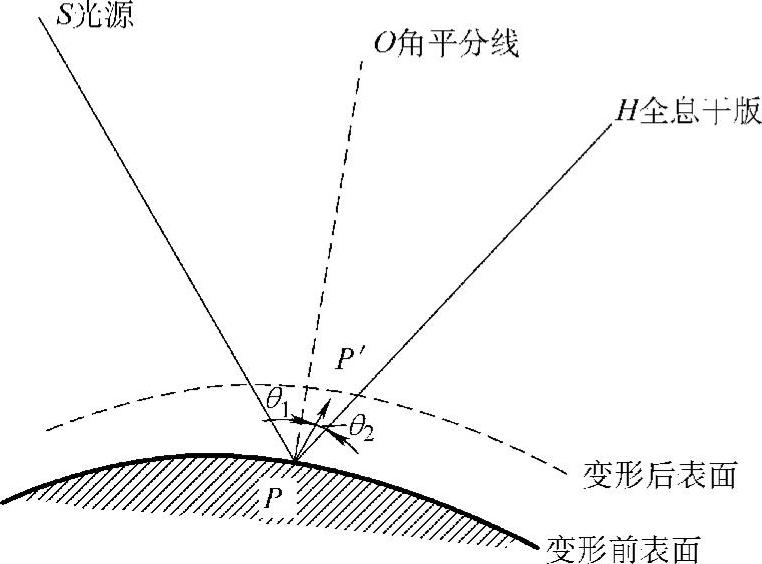
图6.2-4 物体变形前后的位移与位相差的关系

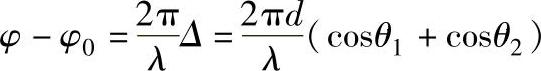
若令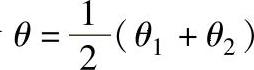，即入射光与反射光夹角的一半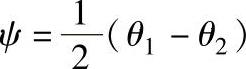，为分角线与位移方向的夹角，则有

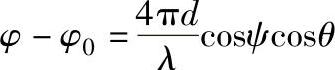
再现象上亮条纹处φ-φ₀=2mπ（m=0，±1，±2，…是亮条纹的级次），代入上式可得

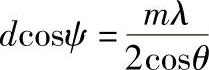
式中 λ——使用的激光的波长。

经过上面的推导，对双曝光法得到的干涉条纹图的物理意义加以说明。通常将入射光与反射光夹角（图6.2-4中的∠SPH）的角平分线（PO）的方向称为灵敏度矢量方向。物体表面任意点处的条纹级数m一般从零级条纹（位移为零的地方）的地方起计数可得，θ角可以根据光路布置得到，所以可计算出该点的dcosψ。此参数代表该点的位移在灵敏度矢量方向的分量。因此，两次曝光全息干涉条纹图给出表面位移矢量在灵敏度矢量方向的投影分量。

如果取照明方向和观察方向与表面法线夹角都相等，即ψ=0，则可以直接得到离面位移。实际使用的光路一般灵敏度方向与表面法线方向夹角很小，通常可以近似认为得到的条纹图就是离面位移的等值线图。在无损检测的实际应用中，通常缺陷在整个视场中占据面积不大，典型的显示是局部的多重环绕的条纹。

图6.2-5是周边固定的方形板受中心集中载荷情况下双曝光法得到的条纹图。周边位置固定其位移为零，条纹级次也为零；条纹级次从周边向中心逐渐增加，中心离面位移最大，达到7级左右。同级次条纹可视为离面位移相同的点，多级环状条纹包围的区域往往代表一个突起区或凹陷区。这在复合材料实际检测中是分层或脱粘缺陷的典型显示。

图6.2-5 固支方板受中心集中载荷时双曝光法的条纹图