MAE和磁致伸缩：研究进展与应用前景

产生磁声发射需具备两个条件，其一是磁化时磁畴的巴克豪森跳跃，另外就是伴随巴克豪森跳跃磁畴有体积应变，它来自于磁致伸缩效应。

众所周知，铁磁材料磁化时具有伸长或缩短的效应，谓之磁致伸缩。通常用磁化方向上材料单位长度的伸长量λ，即磁致伸缩系数来表征磁致伸缩的大小。对钢铁材料，λ＞0，称正磁致伸缩的材料；像镍等，λ＜0，称负磁致伸缩系数的材料。磁致伸缩系数λ随磁化场变化，饱和磁致伸缩系数用λ_s表示。对晶体来说，各方向磁致伸缩系数不一，易磁化轴方向最大，磁致伸缩是各向异性的。

如图5.5-3所示，以90°畴壁分割的畴，未磁化前各畴磁化方向皆为易磁化轴方向，该方向磁致伸缩系数为λ_s。磁化时作巴克豪森跳跃的畴，其磁化方向从易磁化轴转了90°，体积压缩，因此伴随巴克豪森跳跃产生体积应变Δε，将以弹性波的形式释放出形变能，这就是MAE。另外，磁畴转动磁化时，也有体积应变，亦相应激发MAE。如图5.5-3c所示，以180°畴壁隔离的畴，磁致伸缩是等效的。因而巴克豪森跳跃前后，磁畴的体积无应变，Δε=0，故无MAE产生。由此看来，MAE来源于90°畴壁的不可逆跳跃和磁畴的不可逆转动，而180°畴壁的不可逆跳跃不产生MAE。这与MBN产生的机制是不同的，MBN主要来自180°畴壁的不可逆跳跃。

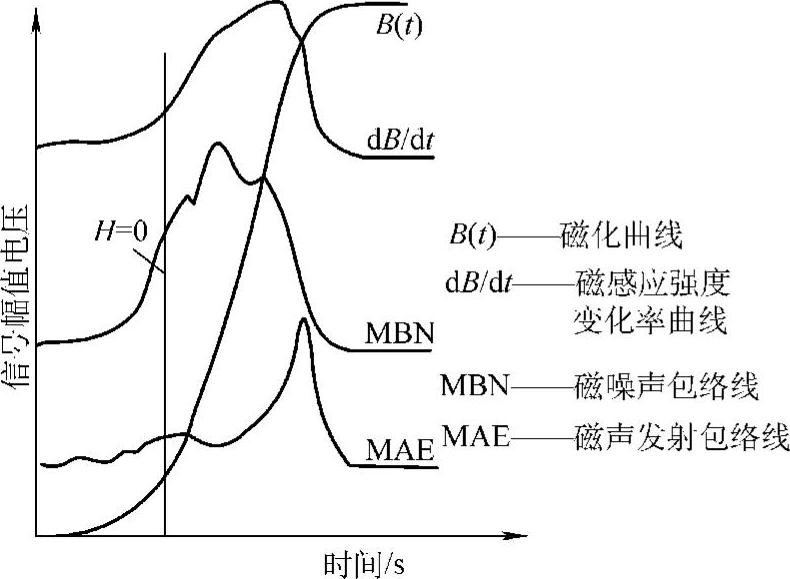
图5.5-2 磁化中MAE和MBN的脉冲包络

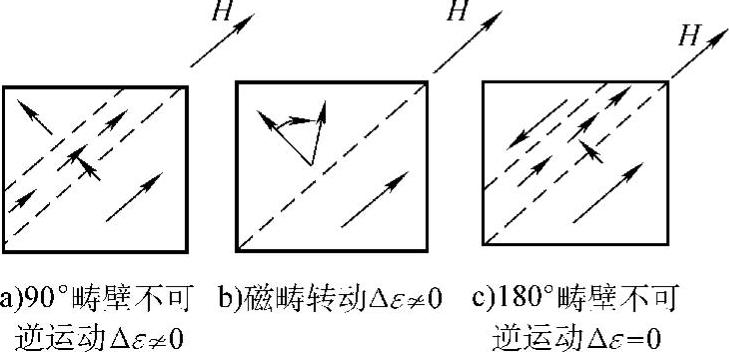
图5.5-3 MAE的产生和磁致伸缩应变(www.xing528.com)

设磁化时某磁畴参与不可逆跳跃的体积为ΔV，体积的应变Δε^∗，跳跃持续时间τ，该跳跃产生的MAE脉冲能量ΔE，可由下式表示

ΔE=CΔε^∗ΔVτ

C是与材料特征相关的系数。材料的磁致伸缩系数λ愈大，Δε^∗愈大，随之MAE愈强。若设单位变化磁场间隔内巴克豪森跳跃的数密度为n（H），每次跳跃释放的平均能量为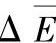，则在一周期T₀内MAE能量的平均值为

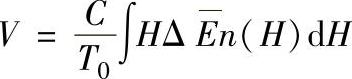
MAE受多种因素的制约，需进行综合分析。