如何选择适合的深度检测方案？

巴克豪森跳跃所产生的电磁信号在材料中传播有衰减现象。信号所在的位置距表面越深，信号传播至材料表面衰减越甚。因此MBN检测中有一个有效检测深度问题。通常将材料某一深度的信号传至表面衰减为原信号的1/e（约为0.37倍）的深度定义为检测深度。

MBN的检测深度由以下几个因素决定。

1）材料的相对磁导率。

2）材料的电导率。

3）信号的检测频率。

对于一个给定频率（f）的信号来说，其检测深度由式（5.4-1）决定：

式中 σ——材料的电导率（1/Ω·m）；

μ——材料的磁导率（H/m），μ=μ_rμ₀；

μ₀——真空磁导率，μ₀=4π×10^-7N/A²；

μ_r——材料的相对磁导率。

如碳钢，μ_r=1000，σ=5×10⁶/Ω·m，对频率为f=6kHz的信号，其S=0.09mm。

一般，MBN信号的检测频率范围为（f₁-f₂），此时引入一个衰减函数D（x），其D（x）为1/e所对应的x即为检测深度。D（x）由式（5.4-2）确定。

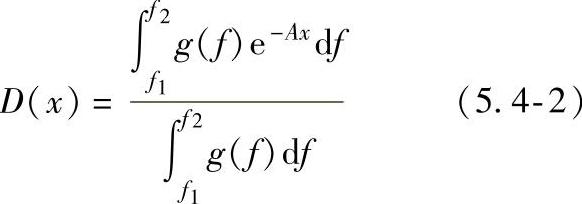(www.xing528.com)

式中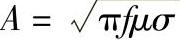

x——距材料表面的距离；

g（f）——频率函数。

对白噪声信号g（f）=1，而MBN为非纯白噪声，各频率段g（f）的取值可从1至0.1，为计算方便，这里取g（f）=1，实际检测深度计算值高出10%～30%。

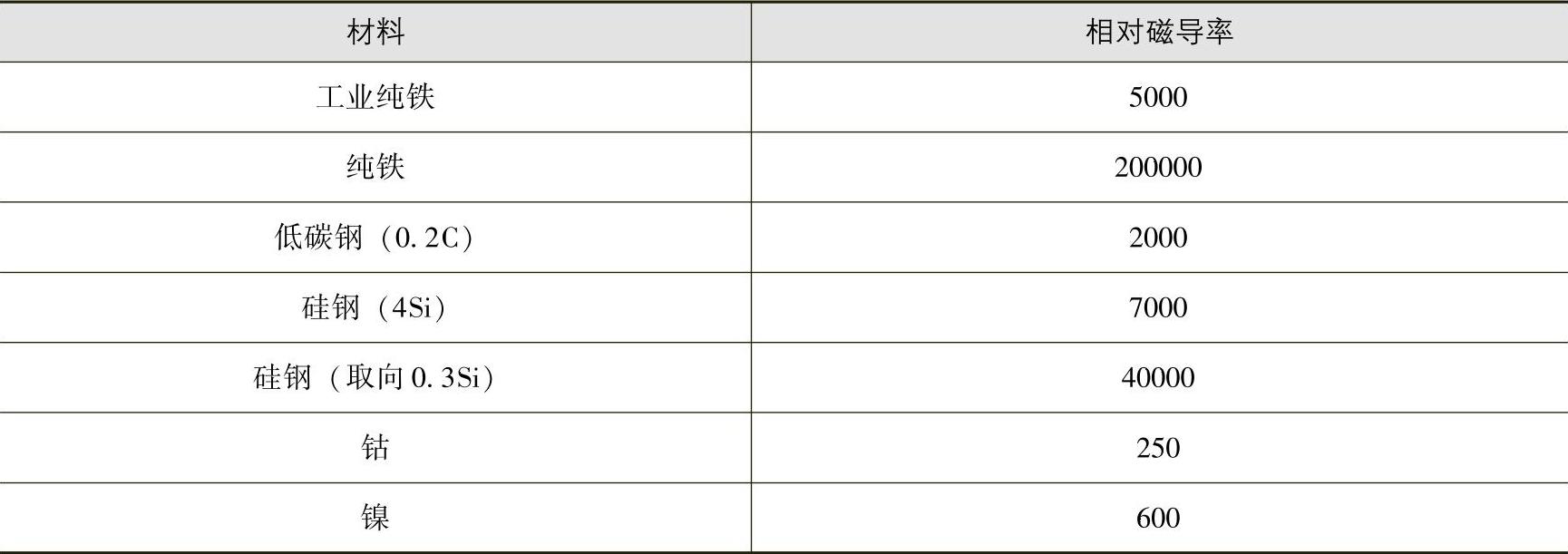
已知材料的磁导率、电导率和信号的频率范围就可求出D（x）。例如材料的μ_r=1000，σ=5×10⁶/Ω·m，频率间隔70～200kHz，则D（x）随x的变化如图5.4-14相对1/e的x值约为0.02mm，即是有效检测深度。图5.4-15则为检测深度与磁导率、电导率的关系。表5.4-1所列为几种材料在几个频率段的有效检测深度。表5.4-2为某些材料的相对磁导率。

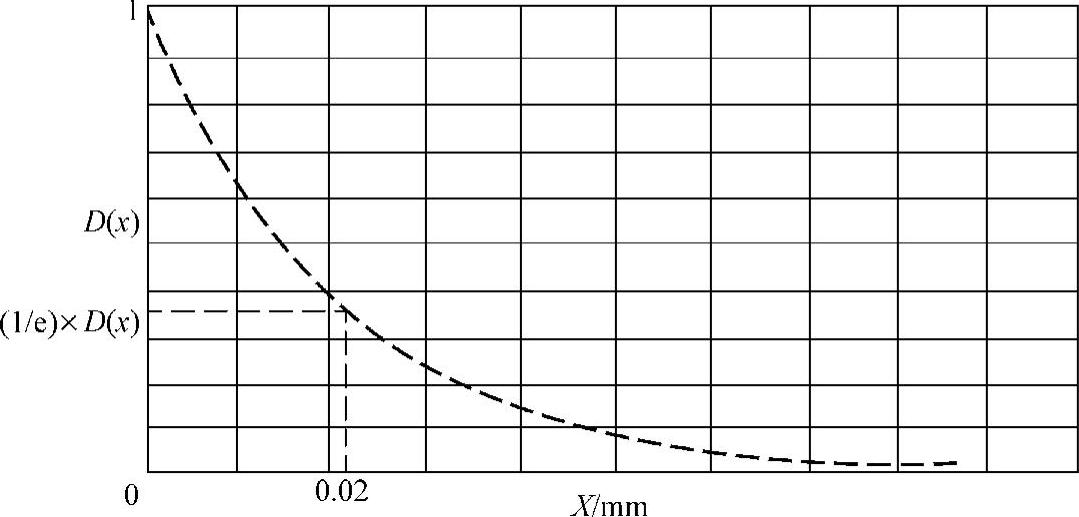
图5.4-14 MBN的衰减函数

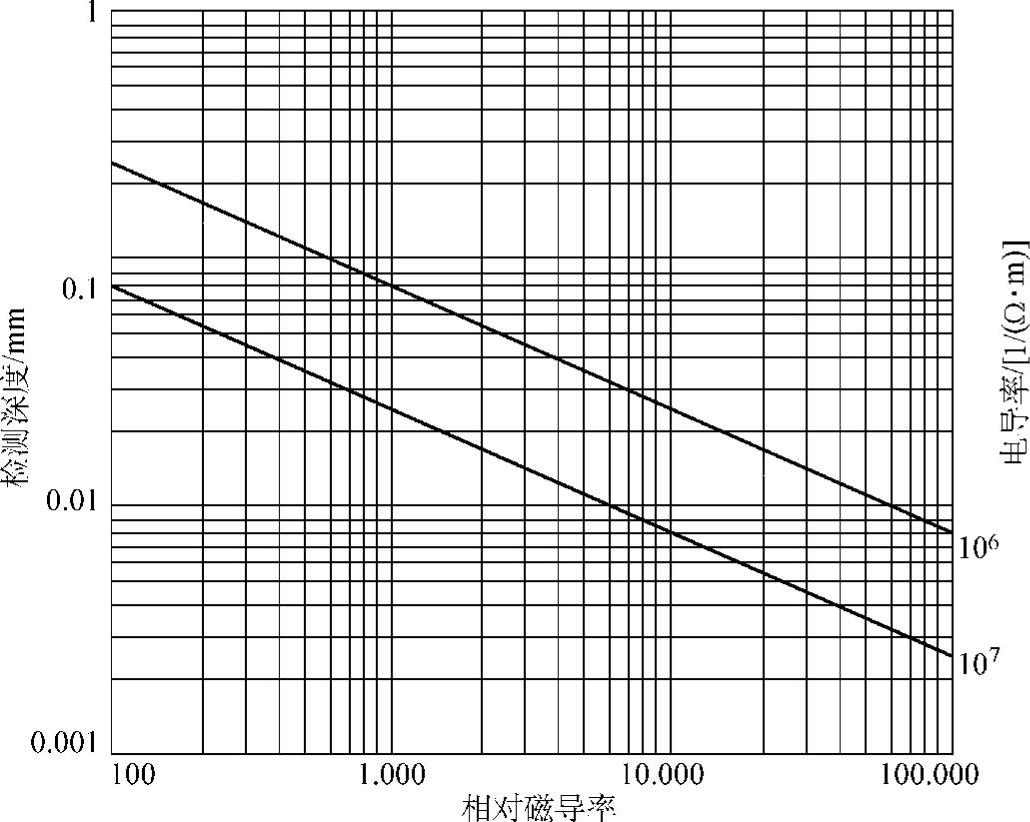
图5.4-15 检测深度与磁导率电导率的关系

表5.4-1 几种材料的有效检测深度 （单位：mm）

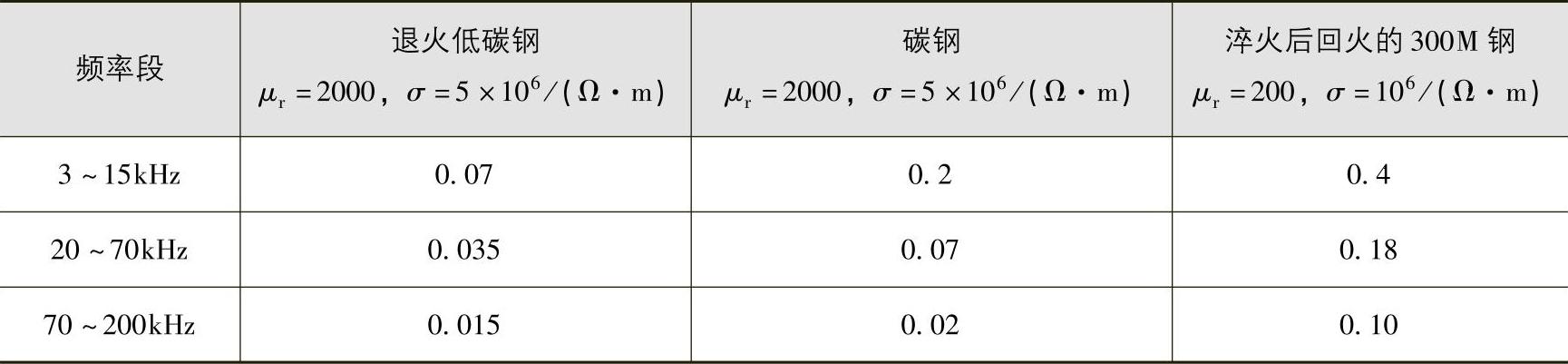
表5.4-2 某些材料的相对磁导率