重要的基础研究工作与基本原理

有关金属磁记忆方法机制方面的研究尚有很多不确定的地方，学术界也有许多争论，本部分主要从磁机械效应的角度对其原理进行解释。

磁机械效应是指由于应力的施加而引起的铁磁性材料磁化强度的变化，这是金属磁记忆方法的基本原理。研究磁机械效应具有较大的工程应用价值，它与诸多技术问题，如磁性材料传感器的开发，无损检测领域中应力检测的磁学方法研究等密切相关。

磁机械效应的研究具有较长的历史。1939年9月，德国人首次在泰晤士河口采用“磁性水雷”攻击带磁的英国舰艇；同年，前苏联舰船遭到德国“磁性水雷”轰击后，前苏联科学院院士Alexan-drov等首次解释了在地球磁场中因振动载荷的影响导致船体金属磁化强度增大的原因。

20世纪四五十年代，Bozorth，Liboutry等对恒定外场下应力加载导致的磁化强度的变化进行了研究，但是并没有得到一致的结论。

最初的研究是建立在磁机械效应完全可逆这个假设的基础上的。假设的核心思想是，既然磁化能改变磁性材料的尺寸，那么磁性材料的应变也可能会引起材料磁化强度的变化。Bozorth对这种设想进行了深入的讨论，Cullity甚至根据Le Chatelier原则进一步研究，得出以下应力-磁感应强度变化式：

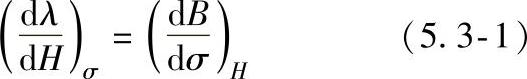
式中 B——磁感应强度（T）；

H——磁场强度（A/m）；

σ——应力单位（Pa）；

λ——磁弹系数，无量纲。

公式的前半部分是在应力为常数的情况下磁致伸缩系数随外磁场的变化率，后半部分是在外磁场恒定的情况下磁感应强度随应力的变化率（SI单位制）。因为B=μ（H+M），而H不是应力的函数，即后半部分等于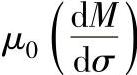。此式成为后来研究磁机械效应的核心公式。

该公式确实适用于较小的可逆变化，对于可逆过程而言，磁致伸缩应变率越大的材料磁机械效应越大。但事实上，磁化的过程是有磁滞损失的，虽然部分可逆，但不可逆的磁畴行为是磁化过程的重要特征。

1949年，Brown发表了他的著名的布朗理论：假设在外磁场较小的情况下，磁化强度的变化是由遵循Rayleigh原理的磁畴运动引起的。

Rayleigh原理在磁学领域的应用描述了微弱磁场下的磁滞行为，即初始磁化曲线。Rayleigh认为，低磁场下的磁滞行为可由式（5.3-2）表达：

B=μ₀H±ηH² （5.3-2）

式中 B——磁感应强度（T）；

μ₀——初始磁导率（H/m）；

η——Rayleigh常数，无量纲；

H——磁场强度（A/m）。

Brown根据Rayleigh原理，并认为外场和应力对磁畴的作用均可等效为对磁畴壁的静压力，得出图5.3-2的应力、外场影响畴壁的理论曲线。

布朗理论存在几个基本的问题。首先，应力是张量，磁场是矢量，具有不同的对称性，不能简单等效。而布朗理论最大的问题在于，它认为磁化强度在拉应力和压应力条件下有相同的变化。这个推论可通过磁畴结构的理论推导得出：一般认为，应力加载只会影响非180°畴壁。在钢和铁中，非180°畴壁就是90°畴壁。将铁磁材料内部90°畴壁分为两种，即应力导致的磁畴运动方向与同轴外磁场一致的90°畴壁，以及运动方向与此方向相反的90°畴壁。假设这两种90°畴壁具有相同的密集程度，那么改变应力的方向只是互换这两种畴壁在磁化过程中所起的作用，拉应力和压应力导致的材料磁化强度的变化应该没有区别。但是很快这个推论就被证实了与实际情况不相符，图5.3-3为Craik和Wood对不同铁磁材料进行试验得到的拉压应力不对称效应的结果。另外，由Brown创建，后来由Brugel和Rimet进一步发展的“畴壁压力”理论还预言，如果应力从最大值卸载，磁化强度将会保持恒定不再变化。同样，这个预言与实验结果也存在差距。

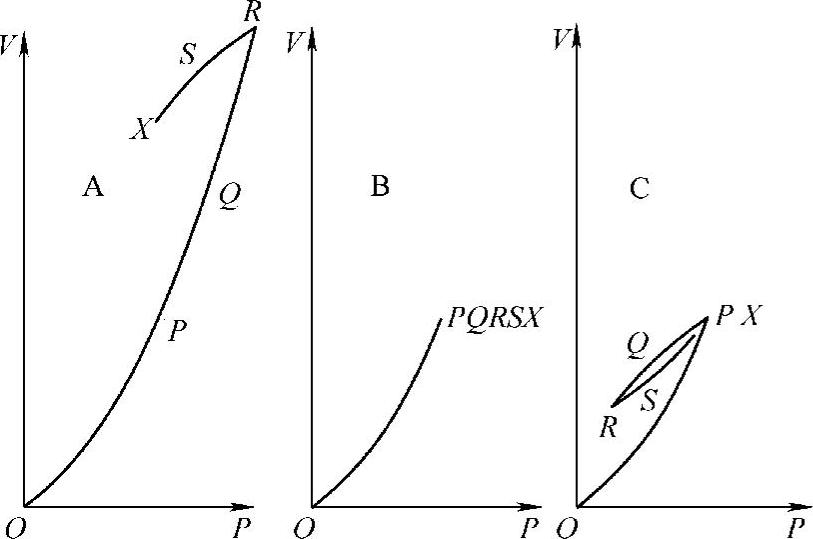
图5.3-2 各类畴壁的行为

A类，拉应力等效于正磁化力的90°磁畴壁；B类，拉应力等效于180°畴壁；C类，拉应力等效于负磁化力的90°畴壁。OP表示磁化力的加载。PQR为加载拉应力，RSX为卸载拉应力。横坐标表示磁化力跟张力等效后的静压力。纵坐标表示试件单位体积内被特定种类磁畴壁侵并的磁畴体积

Craik和Wood根据他们的试验结果得出结论，认为应力对磁化强度的影响不能用简单的磁畴壁运动理论解释，指出在应力作用下磁畴结构发生了不连续的变化，任何磁机械效应的理论必须考虑到这一点。

随后，Birss也根据试验结果给出了许多有关磁机械效应机理的重要认识。他认为，由应力加载导致的90°畴壁所承受的静压力，其作用包含三个过程，即：引起磁畴壁的运动，改变畴壁节点的能量，以及造成磁畴结构的不可逆变化。而Brown理论只描述了上述三个过程中的第一个过程。

1970年到1980年间，主要是发现各种不同材料的磁机械特性。20世纪80年代，Bozorth和Wil-liams获得了应力作用下坡莫合金的磁化曲线，并且发现，施加39MPa的应力后的磁化曲线，十分接近坡莫合金的非磁滞磁化曲线，磁机械效应的研究有了新的进展。

1984年，Jiles和Atherton等人提出建议，认为循环施加的应力对磁性材料磁化强度的影响是一个剩余磁化强度向非磁滞磁化强度不断靠近的不可逆过程。文章没有给出定量的分析，只是定性地推测磁感应强度的变化可能与初始磁感应强度和非磁滞磁感应强度之间的间距成正比。这就是他们提出的接近原理概念。

接近原理随后得到了试验证明，图5.3-4、图5.3-5为Pitman的试验结果。

Pitman工作的独特之处在于，他研究了不同剩余磁感应强度在同一外场下的（dB/dσ）H值。即：80A/m外场下，剩余磁化强度接近正剩余磁化强度时的（dB/dσ）H值，剩余磁化强度接近负剩余磁化强度时的（dB/dσ）H值，以及剩余磁化强度位于初始磁化曲线起始点接近退磁状态时的（dB/dσ）H值。试验发现，应力加载导致的从正剩余磁化强度和从负剩余磁化强度变化的结果几乎镜像对称。而初始磁化强度接近非磁滞状态的试样，其磁化强度的变化量要比前两者小得多。所以，在相同外场和外加应力的作用下，磁化强度变化的方向，由试件的初始磁化强度在非滞磁化曲线的上方还是下方决定。(www.xing528.com)

Maylin和Squire的试验结果进一步证实了剩余磁化强度从主磁滞回线上偏离的实验结果。但是他们发现，这些结果只适用于初始位置在对称磁滞回线上的点。在非主磁滞回线上（非对称），在应力作用下，磁化强度趋于某一平衡值，该值与非磁滞磁化强度不符合。他们的结论是，有三个因素决定磁机械效应变化方向和大小：

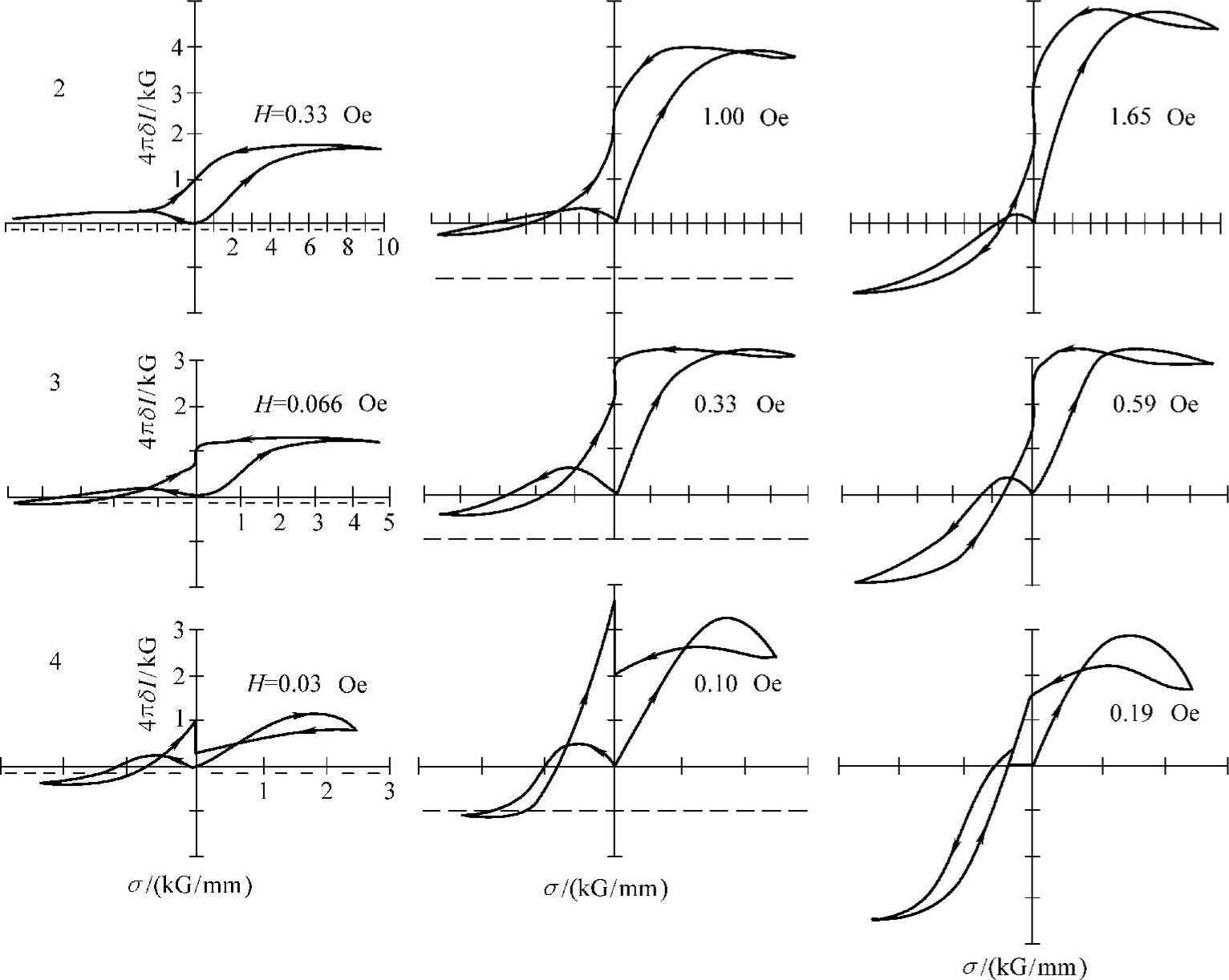
图5.3-3 软铁、普通硅铁等方硅铁材料的应力磁化曲线试验结果

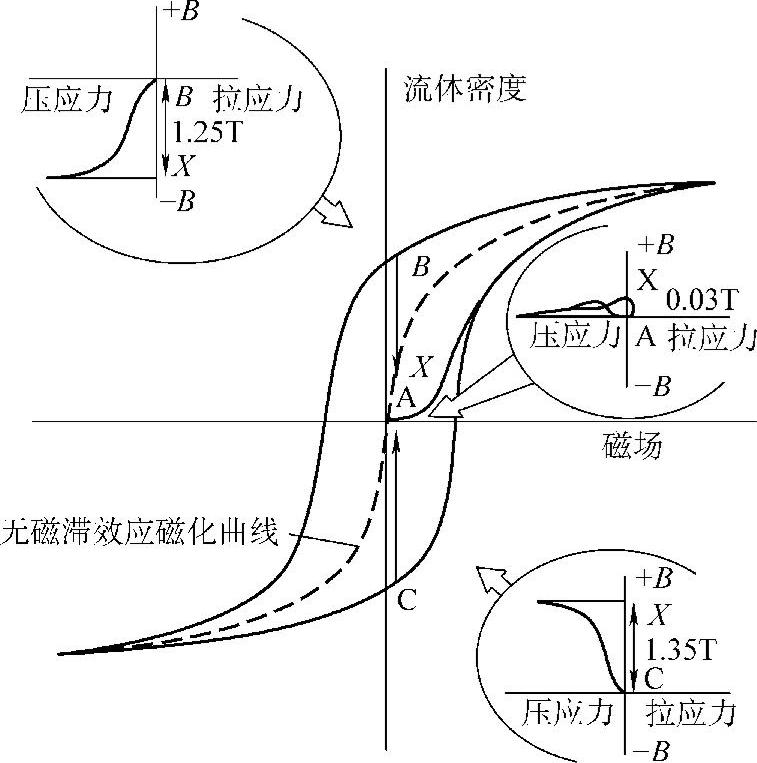
图5.3-4 剩余磁化强度的选取位置

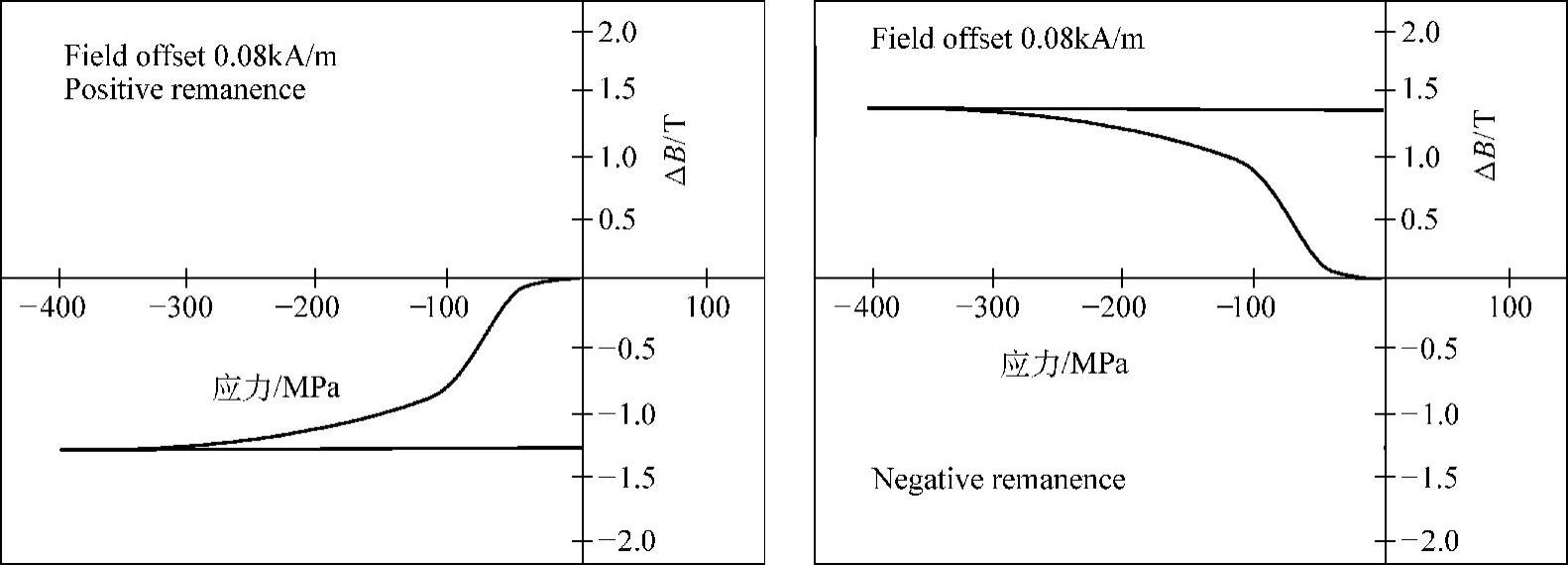
图5.3-5 正负剩余磁化强度试样的镜像对称结果

1）磁化强度与非滞磁化强度的距离（位移）。

2）该位移对应力的敏感程度（接近速率）。

3）非滞磁化强度本身随应力的变化。

1995年，Jiles提出了他的磁机械效应理论，仍然认为应力的作用可等效为一外加磁场的作用，但Jiles是从能量的角度进行分析的。

应力加载使材料沿非磁滞磁化曲线系统能量增加的值为

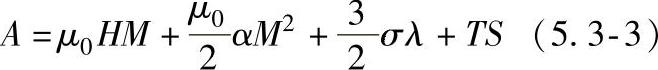
式中 A——系统能量的增加值（J）；

μ₀——真空磁导率，取4π×10^-7H/m；

H——外磁场（A/m）；

M——磁化强度（A/m）；

σ——应力（MPa）；

λ——磁致伸缩系数，无量纲；

T——温度（K）；

S——熵（J/K）；

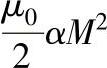——系统自耦合能量（J）。

α是材料内部单个磁性单元对磁化强度的结合能力，无量纲。

等效场导致磁化强度的变化，因此等效场由能量对磁化强度求导得到：

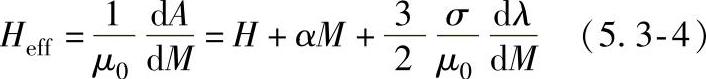
其中由应力加载引起的场为

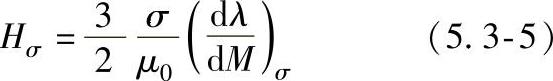
综上所述，有关磁机械效应的研究工作基本上解释清楚了在微弱磁环境下，均匀应力引起的磁场变化情况。显然均匀应力作用下的磁机械效应和金属磁记忆现象并不相同，从应力分布的角度讲，金属磁记忆现象中应力分布是非线性的，而且实际工程应用中的应力集中产生的磁场畸变现象时，外部的磁场也不再仅仅局限于微弱的地磁场。但是，上述研究工作是力磁耦合的基石，为后续研究非线性应力分布的磁机械效应奠定了基础。