对于表面裂纹来说,对材料或构件力学性能影响最大的形状参数是裂纹的深度,裂纹深度如何影响漏磁场的分布,怎样从检测的信号中获得裂纹的深度信息就成了漏磁场检测理论和实际应用研究中最重要的内容,也得到了比较一致的结论,几乎所有的理论和试验结果都支持这样的观点:在一定范围内,对于同样宽度的裂纹,检测到的Sy(p-p)值和裂纹的深度成线性关系,这也成为漏磁场检测量化缺陷的重要理论依据。
实际的检测中可以利用已知人工缺陷的线性关系来量化未知的缺陷,但问题是实际构件中裂纹的宽度不可能相同,其次实际裂纹的形状也不可能和得到线性关系的矩形槽一样。要真正实现检测结果的量化,必须考虑上述两个问题。
1)宽度的影响作用,在深度的量化中考虑宽度影响的唯一方法是将不同宽度的裂纹转化为相同宽度的裂纹,然后利用线性关系进行量化。
图5.2-24是45钢内部磁场强度为9000A/m时,对0.2mm深,不同宽度的矩形槽的漏磁场通过计算得到的Sy(p-p)值:
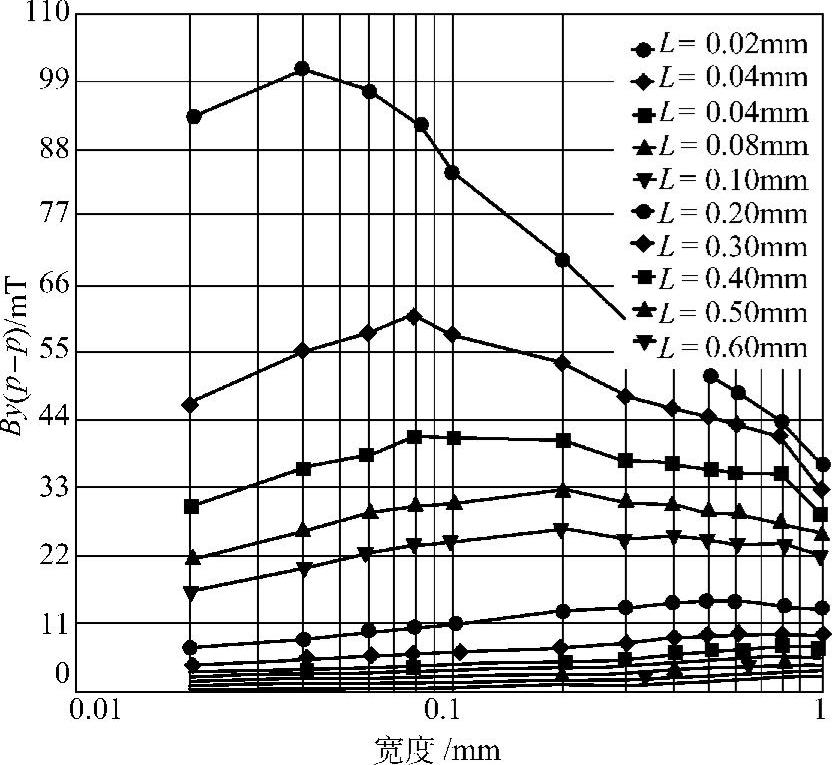
图5.2-24 对于不同的提离值(L),矩形槽宽度不同时Sy(p-p)值变化曲线
可以清楚地看出:
2)宽度不同时,Sy(p-p)值并不是单纯地增大或缩小,而是首先增大,然后变小。提离值不同时,宽度的影响规律基本相同。
3)上述先大后小的规律,在不同提离值大小时也不尽相同,这突出地表现在其拐点位置的变化,也就是说,其最大值随提离值的变大对应的缺陷的宽度值变大。经过认真的计算,发现拐点位于提离值两倍的宽度处。
上述结论在改变诸如磁化强度、矩形槽深度和材质(如铸铁)的情况下具有较好的一致性。
基于上述结果可以提出宽度的影响模型:
1)对于同样深度的矩形槽,当传感器的提离值为L时,矩形槽的宽度为2L时,检测到的Sy(p-p)值最大,记为Sy(p-p)max。
2)宽度的影响可用传感器的提离值和矩形槽的宽度之间的比值k来表述:
By(p-p)=By(p-p)max×k (5.2-9)
当宽度w小于等于2L时:

当宽度w大于2L时:

α、β的取值与提离值大小有关,通过对上述计算数据的分析,可按表5.2-1取值。
表5.2-1 α、β的取值
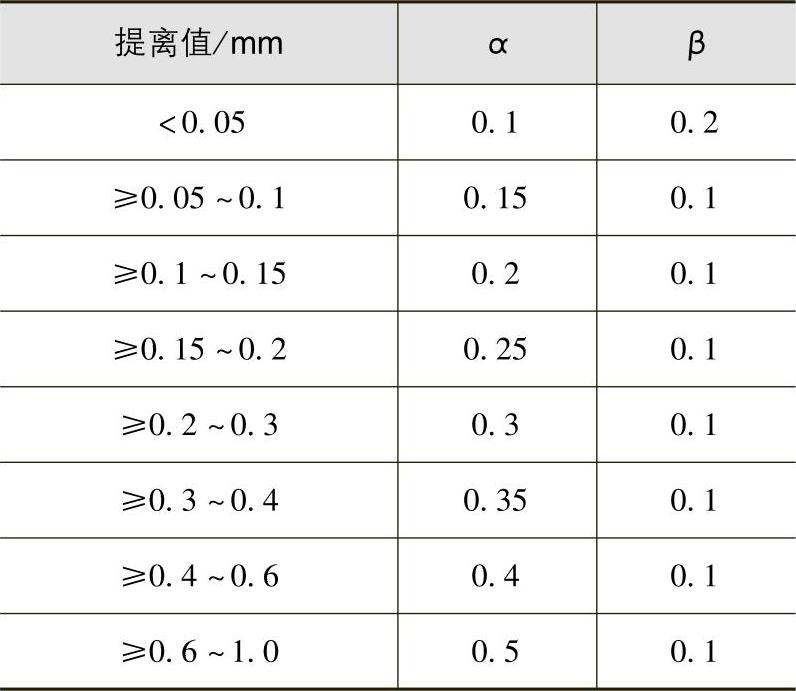
图5.2-25是试验结果和模型计算结果的比较。
利用上述模型就可以实现不同宽度和深度矩形槽的量化。量化按下面步骤进行:
1)在同样外加磁场强度、同样提离值下,同样宽度裂纹的By(p-p)值和裂纹的深度d成线性关系,可记为(https://www.xing528.com)
By(p-p)=c+b×d (5.2-12)
式中 c——常量,随提离值、磁化状态、宽度等不同而变化;
b——线性系数,随提离值、磁化状态、宽度等不同而变化。
(实际检测中,上述关系一般是通过人工缺陷获得。)
2)对线性关系按宽度为提离值的两倍大小进行修正
假定传感器的提离值为L,首先将线性关系By(p-p)=c+b×d修正为宽度为2L时的线性关系,具体方法如下:
假定人工缺陷的宽度为w,
若w≤2L,则线性关系变为
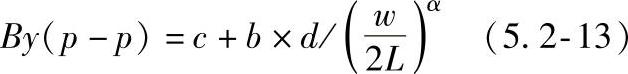
若w>2L,则线性关系变为

式中α和β值的选取按照表5.2-1的规定。
式(5.2-13)和式(5.2-14)就是修正后的线性关系。
3)把检测到缺陷的By(p-p)值按宽度为2L的裂纹进行修正。
假设检测到的裂纹宽度为w1,对应的峰-峰值为By(p-p),若w1≤2L,By(p-p)修正为
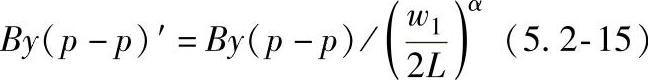
若w1>2L,By(p-p)修正为
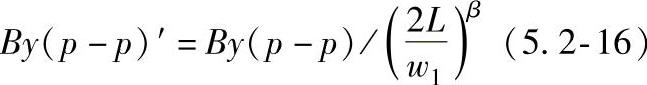
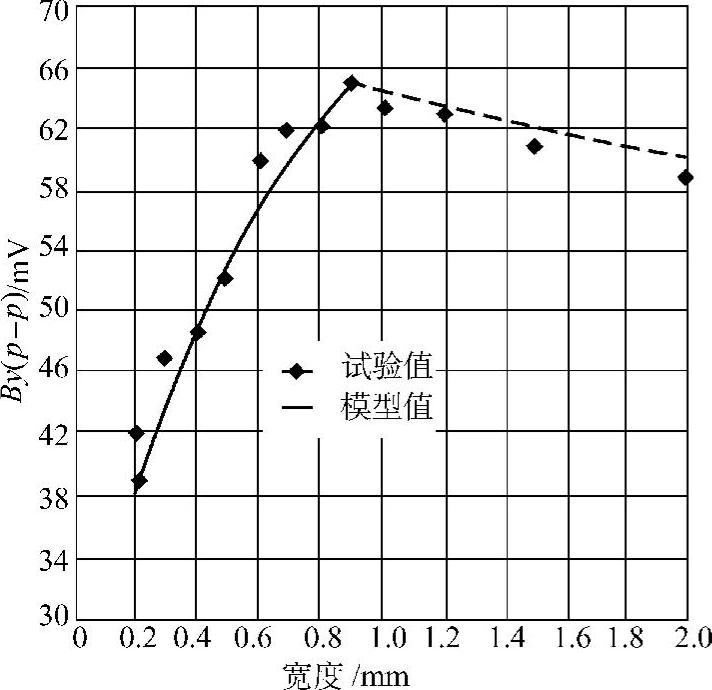
图5.2-25 试验结果和模型计算结果比较
4)把修正得到的By(p-p)′值按量化式(5.2-15)或式(5.2-16)计算得到深度信息d。
上述量化仅适用于矩形槽,但是对于其他表面裂纹的量化有一定的参考意义。由于实际的裂纹不可能有如此规则的形状,必须考虑其形状参数。数值模拟的结果显示,对于规则的等腰三角形的表面裂纹,可以用开口宽度的1/3来修正;对于实际的裂纹,由于实际的形状非常复杂,又有很大的随机性,很难得到非常准确的结果。对于疲劳裂纹和焊接热裂纹的试验结果表明,当用开口宽度的1/6或1/7对检测到的By(p-p)值加以修正时,可以得到较小的量化误差。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




