量化裂纹宽度方法探究介绍

漏磁场检测的研究大都不太重视宽度的影响作用，宽度量化的研究工作不如深度研究得透彻。20世纪70年代末，只有Lord和Hwang开展过一点工作，在矩形槽的形状参数对漏磁场影响的研究中，通过少量的计算数据他们推测，漏磁场By分量两个峰之间的横向距离和裂纹的宽度存在一定的线性关系。

最近的研究表明，漏磁场的By分量包含有裂纹宽度信息，这样就非常幸运地能在不增加检测复杂程度的情况下，同时实现裂纹宽度和深度的量化。横向距离Sy（p-p）的定义为漏磁场By分量最大和最小值之间的横向距离，如图5.2-21所示。

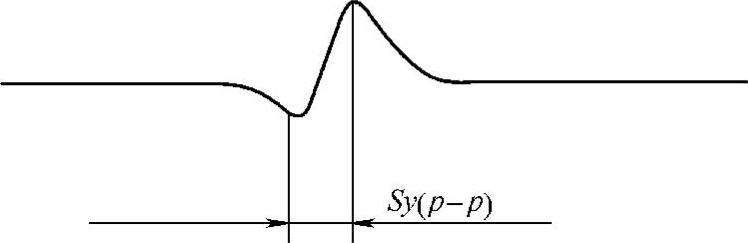
图5.2-21 漏磁场By分量和横向距离Sy（p-p）的定义

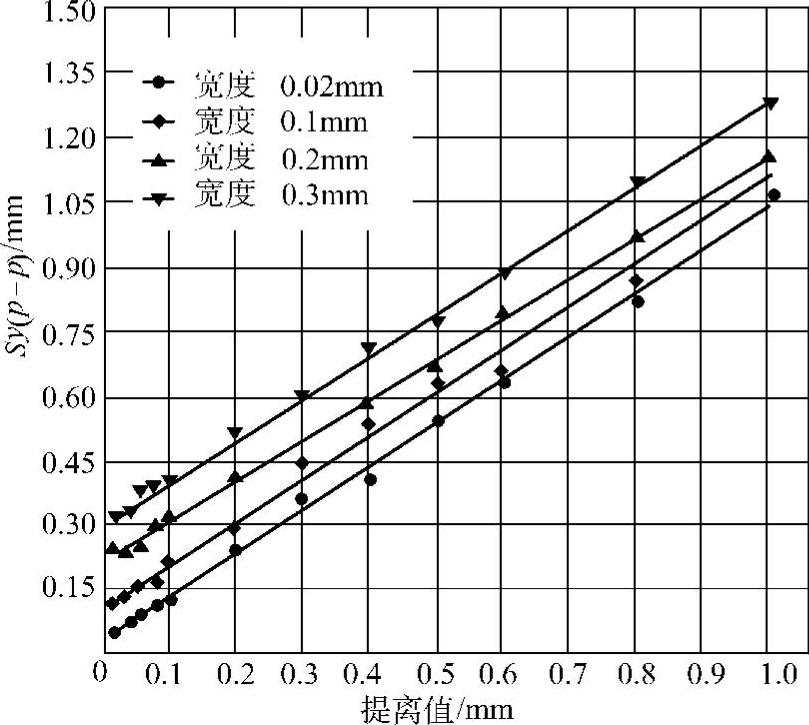
图5.2-22 Sy（p-p）和矩形槽宽度及提离值的关系

图5.2-23 Sy（p-p）和矩形槽宽度及提离值的关系

在分析大量物理试验和数值试验数据中，我们发现，By峰间距Sy（p-p）不仅与宽度有关，还与传感器的提离值有关，Sy（p-p）、提离值L、宽度w存在一定的函数关系：

Sy（p-p）=f（L，w） （5.2-4）

图5.2-22和图5.2-23是数值计算得到的数据，矩形槽的深度为0.2mm，宽度从0.02mm到1.00mm，提离值从0.02mm到1.00mm，施加的磁场强度为9000A/m，其变化规律显示Sy（p-p）值和矩形槽的宽度有很好的线性关系。

对上述数据拟合得到的结果为(www.xing528.com)

Sy（p-p）=1.008w+0.995L+0.009 （5.2-5）

结果非常接近

Sy（p-p）=L+w （5.2-6）

如果用式（5.2-6）来代替式（5.2-5）可以省去系数带来的不便，更直接地反映出三者之间的关系，而由此简化带来的系数误差仅为0.8%和0.5%，常数0.009相对于提离值是一个小量，可以忽略。

对于自然缺陷检测结果也同样得到了上述结论。

式（5.2-6）的意义不仅仅在已知检测条件的情况下可量化裂纹的宽度，它还可以用来确定实际检测中传感器的提离值大小。实际检测中，出于保护传感器的目的，一般都将检测器件封装起来，很难用常规测量的方法来确定它和试件表面的距离。利用式（5.2-5）可以非常简单地得到传感器的提离值大小，对于一定的扫查速度来说，一个已知宽度为w的人工矩形槽，其Sy（p-p）可以通过测量缺陷信号的两个峰间的时间来确定：

Sy（p-p）=vt （5.2-7）

式中 v——传感器的扫查速度；

t——检测到的缺陷漏磁场By分量两个极值的时间差。

则传感器的提离值为

L=v×t-w （5.2-8）