漏磁场的理论计算方法

漏磁场分布计算采用了解析法和数值法两种方法。

1.解析法

用解方程的方法解出所求的量是解析法的实质，而确定可解的、反映客观规律的数学模型是其中的关键。1966年，Sheherbinin和Zastsepin最早给出漏磁场简单的解析方程，也就是磁偶极子模型。他们认为，缺陷的漏磁场由极性相反的偶极子产生，如图5.2-8所示。以二维的矩形槽为例，两个磁偶极子位于缺陷的两侧，磁荷密度为-Q和+Q，在空间一点P（x，y）点产生的漏磁场为：

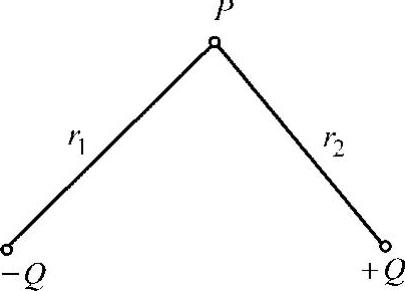
图5.2-8 磁偶极子模型

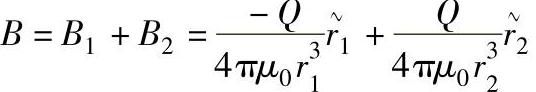
式中 μ₀——真空中的磁导率。

可以看出，磁偶极子模型是经典电磁理论中空间电荷产生电场的一个推广。这个模型较好地解决了漏磁场的空间分布问题。但磁偶极子模型是对复杂的磁问题的简化，当边界条件恶劣时，如缺陷形状复杂，这一模型就遇到了难以克服的障碍——无法确定磁偶极子分布：磁偶极子的分布是和材料磁非线性、磁化强度、缺陷的形状密切相关的。为解决这些问题，后续的研究中大量采用了数值方法。

2.数值方法

漏磁场的本质实际上是缺陷引起的电磁场的畸变，要从场的角度了解它的特性，应求助于现代电磁学。现代电磁学有关电磁场的理论是以麦克斯韦方程为基础的，麦克斯韦方程的微分形式为：

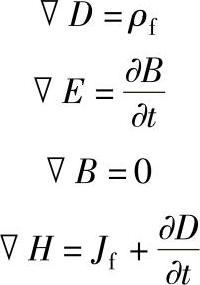
式中 D——电位移；

ρ_f——自由电荷密度；(www.xing528.com)

E——电场强度；

B——磁感应强度；

H——磁场强度；

∇——计算符；

J_f——自由电流密度。

要在三维空间内解决上述时变问题，除极个别的情况以外，用解析方法求解几乎是不可能的。为了解上述问题以及和它类似的力学、机械等方面的问题，人们创造了数值方法。数值方法主要可分为有限差分法、镜像法、积分法和变分法，变分法的现代形式就是有限元法。随着大型计算机的出现，数值法变得越来越引人注目，成了现代科学技术发展中不可缺少的工具。

在漏磁场的数值计算中，主要应用了有限元法。有限元法的优点在于：

1）极大的灵活性，它可以通过不同形状的单元的划分，满足任何形状的边界和交界面。

2）它所得到的代数方程组具有对称正定的系数矩阵，大大简化了线性方程组的求解过程。

3）较为容易引进边界条件，使编程的要求得以简化。

大量的研究表明，对于非线性的、具有复杂边界和形状的缺陷漏磁场问题的求解，数值计算是唯一可行的方法。