微波测量悬浮体浓度的方法探讨

悬浮体是指液体和与其不相溶的某种固体微粒的混合体。通常把液体称为基质，把固体微粒称为悬浮质。为了得到悬浮体浓度与微波衰减量之间的定量关系，假定悬浮体是由基质层与悬浮质层组成，其物理模型如图4.4-31所示。悬浮质的厚度d₁为

d₁=d-d₀

式中 d——悬浮体厚度；

d₀——基质层厚度。

若用W、W₀和W₁分别表示面积和S₀的悬浮体、基质层和悬浮质层的质量，ρ、ρ₀和ρ₁表示相应层的密度，则各层的质量分别为

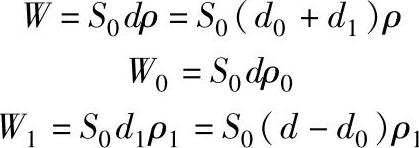
由以上三式，得

W=W₀+W₁=S₀（d₀ρ₀+dρ₁-d₀ρ₁）

根据浓度的定义，有

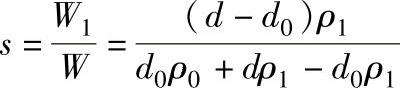
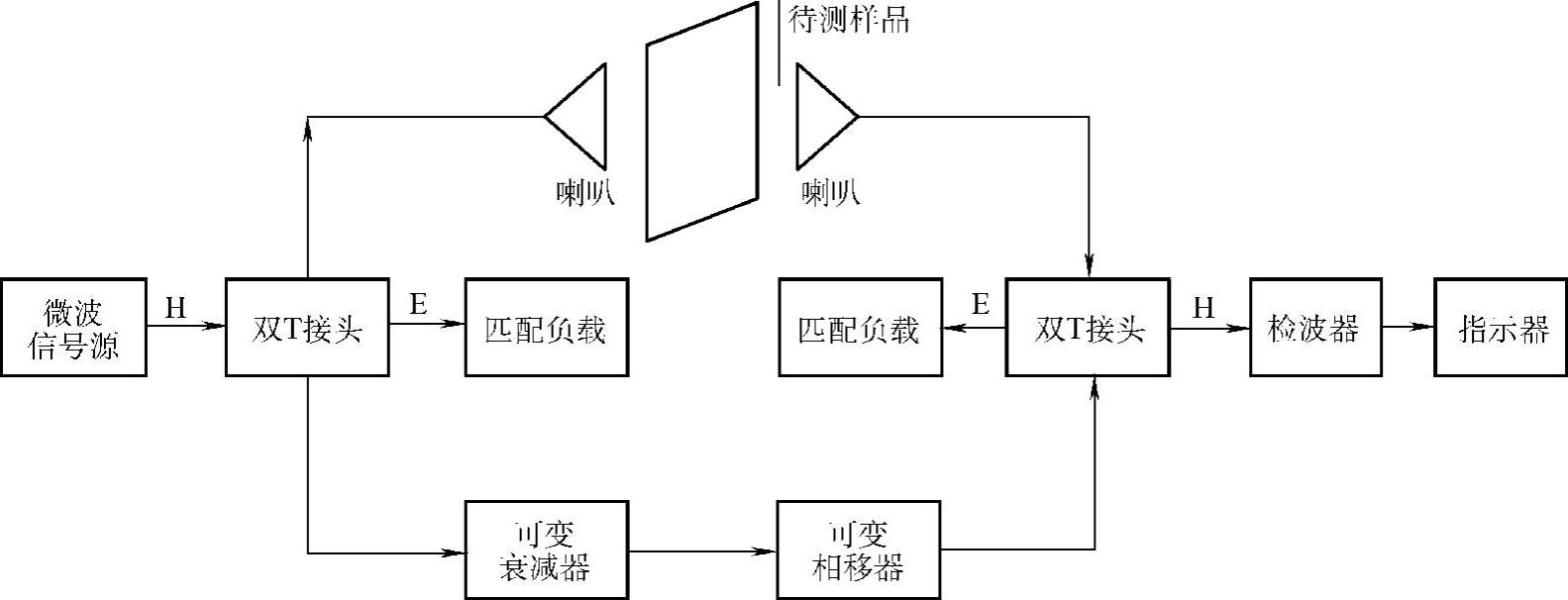
图4.4-30 双T平衡桥路法测湿仪方框图

(www.xing528.com)

图4.4-31 悬浮体的物理模型

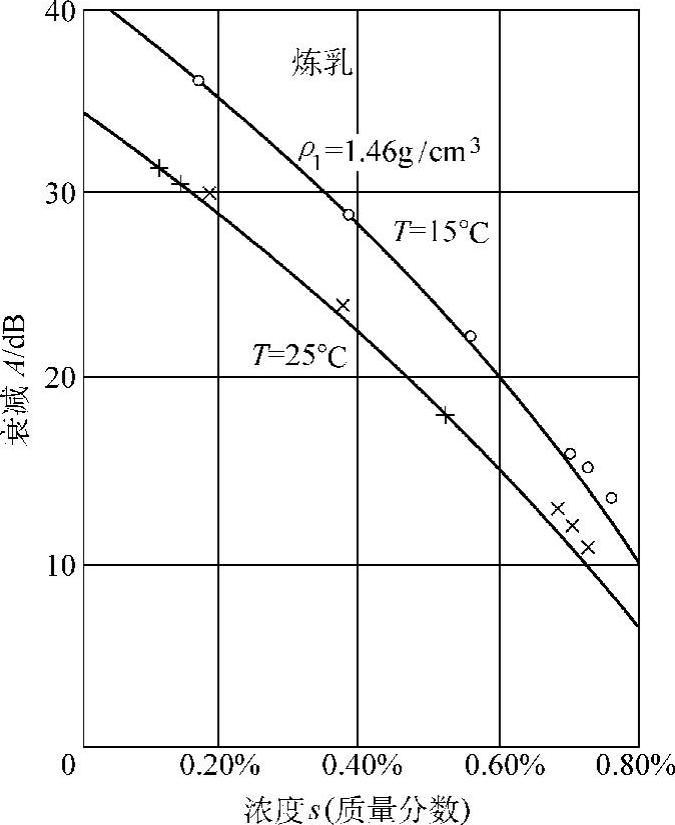
图4.4-32 炼乳的浓度和衰减的实验曲线

悬浮体浓度测量可选用图4.4-30所示的双T平衡桥路法电路。悬浮体的物理模型如图4.4-31所示。在温度为15℃和25℃时，测得密度ρ₁=1.46g/cm³的炼乳的浓度s和微波衰减的关系如图4.4-32所示。

这种方法可用于乳类产品的生产、水泥粘合剂、化工的中间生产过程和其他悬浮体浓度的测量。

微波通过悬浮体之衰减为

A=αd=α₀d₀+α₁d₁=α₀d₀+α₁d-α₁d₀

式中 α、α₀和α₁——悬浮体、基质层和悬浮质层的衰减常数；

当A＞＞A₁且基质为水时，经过变换，最终有

式中 A₀、A₁和A——微波通过厚度为d₀的基质、厚度为d₁的悬浮质和厚度为d的悬浮体的衰减量。

由此可见：某种悬浮体对微波的衰减A与浓度s之间有一定的函数关系：s=f（A）。因此，通过微波衰减的测量，可以测定悬浮体的浓度。