无限长导电圆棒穿过线圈

阻抗

1.关于特征频率的概念

在大多数电磁场问题中，关于动态磁场与感生电流交互作用的分析均涉及非常复杂的数学方法，对于绕在圆柱形固体均质试件上的圆形线圈的特定情况，麦克斯韦（Maxwell）方程的数学解是含宗量A的贝塞耳（Bessel）函数，宗量是一个特征数，它决定着贝塞尔函数的值（犹如角度θ可用来确定三角函数sinθ或cosθ的值一样），在本情况下宗量A可表示为

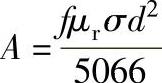
式中 f——涡流的频率（Hz）；

σ——材料的电导率[m/（Ω·mm²）]；

d——圆柱形试件的直径（cm）；

μ_r——材料的相对磁导率。

为便于穿过式线圈涡流检测分析，选择试验频率f使宗量A等于1，此时的频率称为特征频率（f_g），可给出为

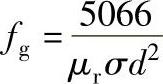
应该注意到，对于特定试件，特征频率既非试验频率的上限也非下限，而且也不一定是应予采用的最佳试验频率，它只是一个参考数或特征数，但它含有除缺陷外棒材尺寸和材料性能的全部信息。任何实际的涡流试验频率f可以以特征频率f_g作为一参考值表示为f/f_g，此时试验频率比f/f_g可表示为

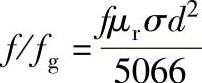
2.关于有效磁导率的概念

在其上绕有线圈的圆棒中磁场强度随其与表面距离的增大而减弱，事实上在圆棒的中心线上是没有涡流流动的。为了简化涡流检测的分析，人们假定外加的磁场强度H₀在试件的整个截面上是均匀而无扰动的，但是，试件的磁化就得用有效磁导率μ_eff来描述，有效磁导率μ_eff：①在试件的整个截面上大小、相位不变，②为一复数，有虚部_{μeff（imag）}和实部_{μeff（real）}，幅值小于1。这样，计算磁化线圈的阻抗或检测线圈（副线圈）的电压时就可以用假定不变的场强H₀与材料常数μ_eff的相乘积来进行。

应该注意到，这样的简化对于很多实际的涡流检测系统并不总是正确的，作为简化的基础包括了：

1）激励线圈在其绕组的整个截面上产生均匀的磁场，实际上即使在线圈中没有试件，磁场分布也是不均匀的。

2）试件是无限长的，端头效应可以忽略，对于长棒，在远离两端处这是很接近的，而对于短试件，端头效应是明显的。

3）试件是圆柱形的，直径d恒定。

4）在整个体积内和在不同的磁化状态下，试件材料的电导率和磁导率为常数，但在铁磁材料中除非采用磁饱和技术，磁导率随磁场强度的不同可有很大的变化。(www.xing528.com)

5）磁化场被假定随时间作正弦变化，频率单一。而在铁磁材料中由于磁化特性非线性，所产生的信号谐波分量的影响是被忽略了。

6）试件填充了线圈的整个空间。

7）在铁磁材料中磁滞效应在这些分析中也被略去。

尽管作为简化分析基础的假设有诸多局限性，有效磁导率的概念还是可使穿透式线圈的试验分析得到很大简化，使用是有理由的，是涡流检测中的重要参数。图4.1-10为μ_eff与频率比f/f_g的关系曲线。

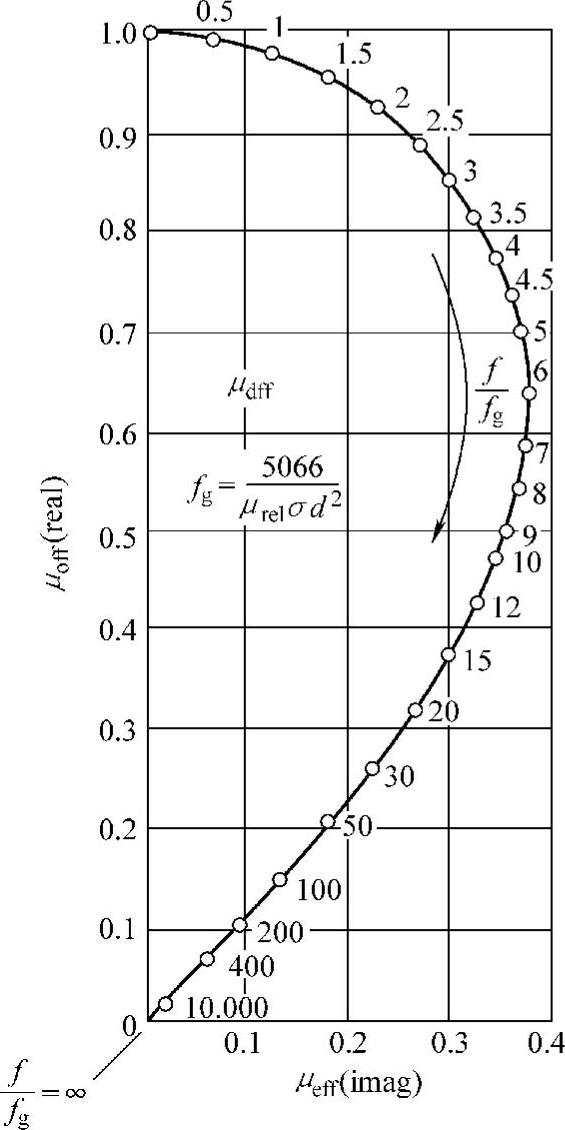
图4.1-10 实心非铁磁性圆棒填充线圈整个空间时有效磁导率的复平面图

3.棒直径小于穿过式线圈内径时的情况

在有效磁导率概念的叙述中假设了试棒直径d完全填充了内径为D的检测线圈（参阅图4.1-1b），但实际上d必须小于D以便试棒能自由地通过线圈，在棒处于线圈中心位置（居中）的情况下，用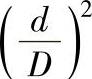表示检测线圈面积被试棒填充的分数称为居中填充因子η。

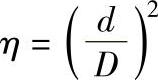
通过计算可以得出，对于电导率为σ的非铁磁性无限长均质圆棒，检测线圈（副线圈）的电压V_sec可表示为

V_sec=V₀（1-η+ημ_eff）

式中 V₀——在线圈中无试样时（d=0）空线圈的电压。设检测线圈匝数为N_s，则

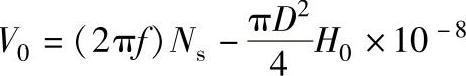
归一化的检测线圈电压可表示为

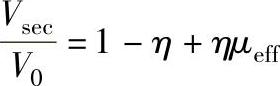
图4.1-11则是含非铁磁性圆棒线圈的阻抗平面图。

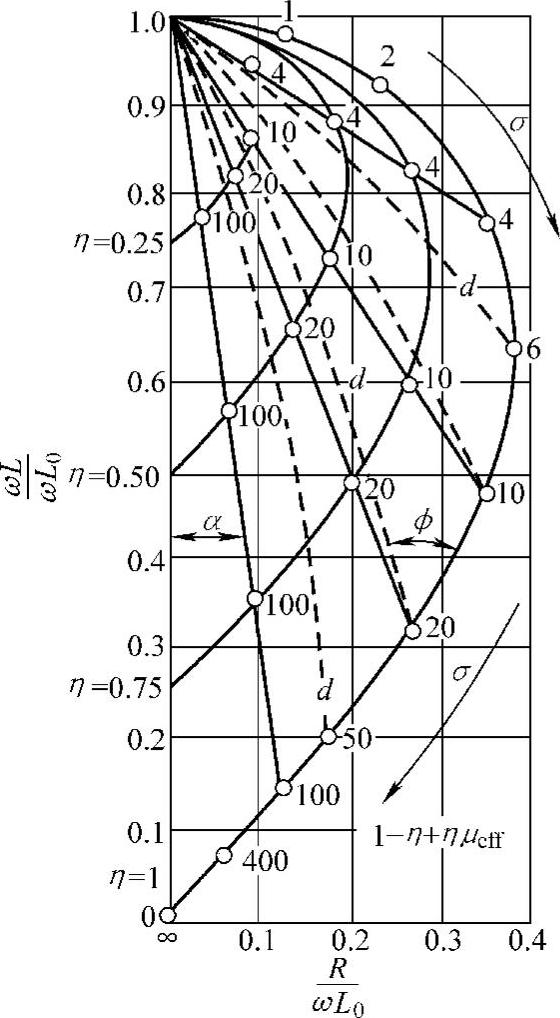
图4.1-11 含非铁磁性圆棒线圈的阻抗平面图填充因子η=0.25，0.50，0.75，1.00，虚线表示直径变化的方向