无损检测：振动分析与应用

振动分析作为无损检测工件的手段由来已久。它不同于通常所指的振动学上的振动测试。振动测试是在现场或实验室对振动系统的实物和模型进行试验和检测。振动测试包括响应测量、动态特性参量测定、载荷识别以及振动环境试验等内容。振动测试的宗旨是，以振动作为产品或工程的一个重要特征，利用振动测试对样机（原形或模型）进行动力特性的研究，把结果作为改进设计的基础和修改数学模型的依据，从而提高产品或工程运行稳定性、安全性和人体感觉的舒适性，提高生产的有效性和精确性，延长产品使用寿命。

无损检测的振动分析，只是作为旋转工件查找工件存在不连续（缺陷）的手段。随着微处理器惊人的进展，在过去的20年间，振动分析这一相对来说较新的技术，很快从特殊的、发展中的阶段进入了普及的、有价值的应用阶段。在20世纪90年代末，美国无损检测学会（ASNT）已将其列入为与常规技术并列的新的无损检测培训与考核专业。

1.检测原理

每一个旋转的机器均具有其各自唯一的独特的振动特征波形。这一特征信号是机器设计、制造及其零件磨损的综合反应。让维护机器的工程技术人员熟悉其振动特征波形，及早发现故障，避免事故，无疑是极为有益的。

（1）振动的正弦波特征振动（简谐振荡）定义为对于某一平衡位置的小振幅的振荡。描述与分析振动，必须涉及正弦波的一系列波形的幅度、频率与相位等概念。正弦振荡的波函数如下式所示

d=Dsin（ωt+φ₀） （3.3-23）

式中 d——瞬时振动位移；

D——最大振动位移（振幅）；

ω——振动角频率，为振动频率f的2π倍；

t——时间；

φ₀——初始相位角。

可以看出，振幅与频率的测量为绝对量值；相位则是以与某一基准相比较的相对值。如图3.3-13所示，波形A与B相位差为90°，A超前B90°；B滞后A90°。

图3.3-13 相对相位图——A超前B90°

旋转机器的振动波形实为一系列不同频率、振幅、相位的正弦波所叠加。采用快速傅里叶变换（FFT）技术可以将该综合波分解为多个元素的正弦波，对其进行物理意义上分析，作为元器件缺陷检测的手段。

以曲轴驱动活塞上下移动的旋转机器为例。假定曲轴的转速为每秒一周（1Hz）。为了描述活塞的运动，必须定义某一参考点，通常以活塞处于中间位置（平衡位置）为参考点，从而活塞位移与时间的关系形成正弦曲线。在开始的时候活塞水平中心线处于平衡位置，波形偏转的幅度为零。如曲轴的转动将活塞向上推，1/4转以后活塞处于顶部极限位置，此时t=0.25s；曲轴继续旋转，活塞向下运动回到平衡位置，此时t=0.5s；当曲轴转至第三个1/4转时，活塞向下运动，直至到达底部极限位置，此时t=0.75s；最后，在末了的1/4转，活塞再次回到平衡的位置，此时t=1s，曲轴完成了完整的一个周期转动。

讨论曲线最大偏移（振幅，此处为活塞最大位移）有如图3.3-14所示的几种方法：一种是用偏移的峰值P描述，假定曲线是对称的，此处为活塞上、下位移，则P=±D（见图3.3-14a）；二是用曲线的峰-谷值描述，峰-谷值=2D。第三种描述的方法是采用方均根D_rms值描述。

方均根值又称有效值，是以能量计算来定义的。存在于图3.3-14a所描述的系统的能量是由如图3.3-14b所示曲线下阴影的面积来描述的。面积在零线以上部分为正，在零线以下是负的。在一个周期内，这两面积相加就等于零。为了避免这一点，将曲线上的每一点平方（即每一点乘以自身的值），在一个周期内，这样曲线就可以描述为如图3.3-14c所示的两面积均为正，且可以相加。将这一值取时间平均，即以周期除以平方相加值，把这已经平方的答案再加以开方即为方均根值，其数学表达式为：

式中 T——一个周期的时间。

当振动位移呈正弦变化时，d=Dsinωt[见式（3.3-23），取φ₀=0]。正弦振动的有效值约为峰值的0.707即

D_rms=0.707D （3.3-25）

图3.3-14 振幅的描述

（2）振动的正弦波描述在给定频率下存在的任何振动可以用单一的正弦波来描述。包括上述曲轴-活塞在内的旋转机器都可以用图3.3-15所示质量-弹簧系统描述。在图3.3-15中，质量的中心线处于正常的静止位置（即振幅的零点）。如果质量被扰动，质量将随弹簧上下振动。若质量振荡的频率f为1Hz，则如图3.3-15c所示，完整的振荡周期为1s（与上述的曲轴-活塞系统相同）；若系统工作频率为2Hz，则在1s内完成2完整周期（见图3.3-15b），周期为0.5s，即

图3.3-15 质量-弹簧系统

图3.3-16 以速度描述振动

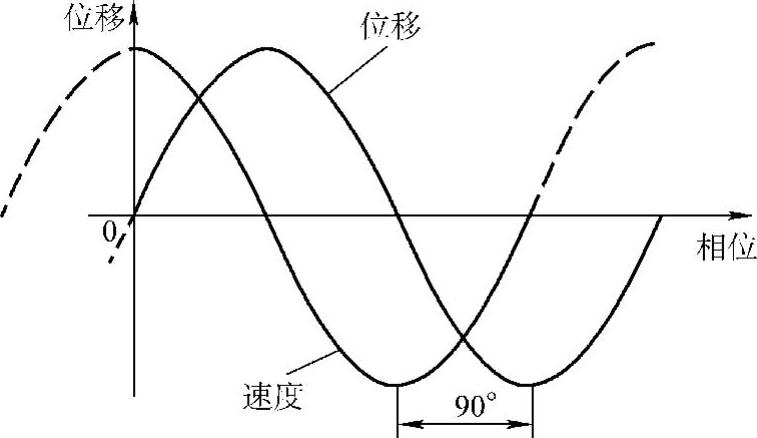
图3.3-17 速度超前位移90°

图3.3-18 加速度

图3.3-19 加速度超前速度与位移

振动的描述除了用位移幅度以外，还可以用速度与加速度。由物理定义得知，速度是时间对位移的微分，加速度是时间对速度的微分。众所周知，正弦的微分导数为余弦，因而正弦波的速度幅值曲线为如图3.3-16所示余弦曲线。正弦波的速度曲线的相位超前位移曲线相位90°，如图3.3-17所示。正弦波的加速度曲线相位则又超前速度曲线相位90°，而与位移曲线相位成180°异相，如图3.3-18和图3.3-19所示。

由于加速度计廉价，且使用方便，在振动问题的幅度测量中常采用加速度计来测量，并以加速度的声强级（dB）或g为测量单位。声强级的单位下文将作进一步说明，g为地球的重力加速度，其值为9.8m/s²。

（3）声强级的应用在声与振动分析中，由于声强的数量级相差悬殊（可达10²¹倍），所以常用对数标度作为声强级（以L_I表示）的量度，即

式中 I_r——为声强的标准基准。

声强级的单位为贝尔（B），实用中贝耳这一单位尚嫌太大，常用分贝，即

1dB=0.1B （3.3-28）

由于声压、振动位移、速度、加速度的幅值平方比才是功率（声强）的比，所以这些量值比例的分贝值为

在声学中，声强的标准基准为10^-12W/m²（即在1000Hz时，一般正常人听觉的最低声强）；声压的标准基准为2×10^-2Pa；加速度的标准基准为10^-5m/s²；速度的标准基准为10^-8m/s。

分贝最早的概念是贝尔实验室为描述电功率在传输电缆中功率损失创造出来的。在电学中（包含振动分析仪器的信号处理中），分贝作为比值仍广泛应用于信噪比的计量，放大器增益或衰减器衰减比的标称等。

由于振动分析中，振幅通常以峰值、峰-谷值或方均根值来测量，而不是用作功率的平方值，因此对分贝值应以20为系数定义，而不是10。表3.3-11列出了振动分析中常用的分贝振幅的线性倍数。需要注意的是，对“-dB”习惯上称衰减多少dB，而不称增益多少“-dB”。

表3.3-11 分贝振幅的线性倍数

（4）振动信号的滤波如果全然没有滤波，用一个仪表测量声或振动，必然把存在于仪表灵敏度范围（如0.025～8kHz）内的所有峰值统统加起来，并像在单一的振幅数那样以dB或mm/s显示其总量值。不内装滤波器只产生单一振幅值显示的装置是廉价的，且它可以指示在该频谱总体内声与振动的严重性，被普遍用于关键机器的周期性监视中。然而，这一未经处理的信号，它所传达的信息是很不够的。例如，不能用它在有不完善齿轮的机器中查找轴承的磨损。所以，必须首先进行滤波，得出我们认为有用的频带范围内的信息。即获取轴承磨损引起的振动频率带内的信息，使其不与齿轮不完善产生的信息混在一起。这就必须应用各种不同的频率带宽的滤波器。

最简单的三种滤波器是：低通滤波器、高通滤波器和带通滤波器。

（5）滤波器的带宽与下降率理想滤波器的性能是在滤波范围内的输出达100%，超过标称边界的信号则全部剔除，即输出为零。实际滤波器不能完全达到这一点，随着信号的逐渐偏离中心频率，通过的能量逐渐降低，如图3.3-20所示。按定义，滤波器的标称边界称为转角频率。在这一频率下，输入信号在到达输出端以前将损失其功率的50%，所以又称半功率点频率。两半功率点（峰值下降3dB，幅度为峰值的）间的频率宽度即为频率带宽。

图3.3-20 滤波器带宽与下降率

滤波器频率带宽以外信号衰减锐度即为滤波器的下降率。它的量值是以倍频带内的衰减dB数来表示的。因此，数值为6dB/倍频带的下降率的滤波器，当输入信号的频率超过上限转角频率时，信号频率每增加一倍，幅度随之减少一半（6dB）；而当输入信号的频率低于下限转角时，信号频率每降低一半，幅度也减少一半。上述的所谓倍频带是指频率上限为频率下限两倍的频带，如从xHz到2xHz等。

振动分析仪采用的均为带通滤波器。滤波器的带宽和下降率决定了分析仪的测量精度和分辨力。

由于振动分析仪测量的是滤波器的输出，它将滤波器频率范围内所有输出量加起来，并把它考虑成滤波器中心频率的幅值。因此，每一滤波器只能得到一个频率下的幅值。为了获得整个频谱的幅频特性（幅度相对于频率的曲线），必须采用其中心频率可以在一定范围内扫查的扫频滤波器，或者采用很多个依频率高低顺序排列的滤波器。

常用的带通滤波器有两类——恒定百分比滤波器与恒定频率带宽滤波器。

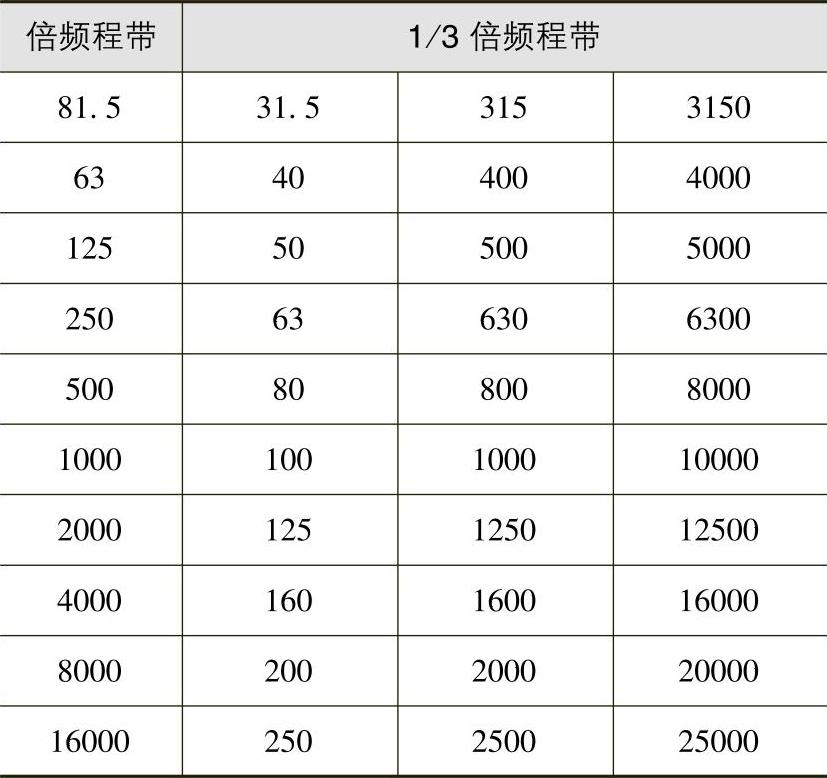
（6）恒定百分比滤波器与恒定频率带宽滤波器恒定百分比滤波器可以调到某一给定的中心频率，用它可以查看存在于正负该中心频率某百分比范围的频率。最常见的恒定百分比滤波器是设计成为以倍频程来表示的，如1/3倍频程、1/10倍频程带宽等。一个倍频程是频率加倍。从2Hz到4Hz是一个倍频程，从4Hz到8Hz是一个倍频程，从8Hz至16Hz又为一个倍频程，依次类推。恒定百分比滤波器的问题是，随着中心频率增大，能通过滤波器频率的数目增加，从而分辨力下降。表3.3-12给出了标准的倍频程和1/3倍频程中心频率。

表3.3-12 标准倍频程与1/3倍频程的中心频率 （单位：Hz）

倍频程滤波器的有效频率带可用下式计算

F_LC=0.707×F_C

F_HC=1.414×F_C （3.3-30）

式中 F_LC——低端转角频率；

F_HC——高端转角频率；

F_C——中心频率。

1/3倍频程滤波器的有效带宽为23%，它的计算是将式（3.3-30）的系数分别代之以0.89与1.12。其他常用的恒定百分比滤波器组是1/10倍频程（6.9%）、1/12倍频程（5.8%）、1/15倍频程（4.6%）、1/30倍频程（2.3%），以及5%、10%与20%频带的。

恒定频率带宽具有一个固定的带宽。倘若某一滤波器具10Hz的中心频率，5Hz的带宽，如果在8Hz与11Hz有两个信号，这两信号的能量将被相互加起来而被看做是在10Hz的单一峰值。在这一情况下的带宽为中心频率的50%，因而不可能精确到如人们所要求的。如果我们考查的在100Hz的5Hz带宽，频率范围将从97.5Hz到102.5Hz。在这一中心频率下，5Hz的分辨力只产生5%带宽。在较高的频率下，误差变得不明显，如果需要较高分辨力，常见的可达到1Hz，对10Hz的中心频率，可看做是将存在于9.5Hz到10.5Hz的所有峰值显示为如同存在于10Hz的单一峰值。现代的频谱分析仪具有0.025Hz或更小的高分辨力。

2.分析程序

（1）用滤波器作诊断图3.3-21示出了用全倍频程和1/3倍频程的滤波器作振动信号的比较。可看到，1/3倍频程的曲线给出较好的振动特征概念。同时还可以看到，用带宽越窄的滤波器，精度越高，图3.3-22是同一振动源用400滤波器（400线谱）的曲线。

图3.3-21 实际全倍频程与1/3倍频程振动数据

图3.3-22 图3.3-21中的数据用400线显示

很显然，为可靠地确定振动和声源，要求频带尽可能窄的滤波器，因为如果高电平的振动信号的频率可以确定得较精确，我们更有希望寻找出这一高电平产生的原因。现代先进的工艺水平已经能用很大数量频带很窄的滤波器实施振动分析。这对于确定什么是噪声或振动机器可能存在的问题很有帮助。表3.3-13列出了旋转机器常见的作用力（外力作用）与其频率。

（2）简单频率分析以图3.3-23所示的系统为例，可能的外力（受迫振动）频率如下：电动机频率=1800/60=30Hz；泵频率=100/300×1800/60=10Hz；齿轮啮合频率=100×1800/60=3000Hz；叶片频率=8×600/60=80Hz。

表3.3-13 作用力及其频率

注：n=1、2、3、…。

图3.3-23 带转速为1800r/min电动机的典型机械系统

显然，诸如齿轮啮合边带、轴承频率以及上述外力频率整数倍的频率均可能存在。图3.3-24示出了在水泵驱动端轴承测量的以加速度计电平计算的频谱。

（3）振动的许可水准上述的例子中已经辨认了各种受迫振动的频率，下一个问题是确定它们是否超过了许可的幅度。一个许可的振动水准是不会因此而导致在任何程度上减少振动机械的寿命，或者造成对周围设备的危害。某些机械设计成有极高的振动许可水平，如岩石粉碎机；而某些装置甚至低的振动水平也极为敏感，如光学系统等。

有四种确定给定机械许可振动水平的方法。最实际的方法是，在机械的关键点坚持定期地记录振动数据多达几年以上。

图3.3-24 典型机械系统的频谱

如果工厂有几台相同的机器，则可以采用第二种确定的方法：假如三台机器有相似的振动频谱，而第四台机器在相同的运作条件下显示较高的水平，就推测第四台机器有问题。第三种方法是，搜集可疑机器的振动数据并送到制造厂请求评定。要注意的是，振动随着机器的运作条件和它的安装而变化。还要记取的是，在某些情况下，操作者可能比制造者更了解有关该机器的振动知识。第四种方法是借助一个基于其他机器经验的标准线示图，如果需要应对其加以完善使其更适合操作者的经验。

振动的水平超过了允许的界限，肯定应该进行考查，直到制造厂给出保证，该可疑设备这水平是正常的。振动的某些频率即使在很低水平也是不能允许的。这点对轴承频率、耦合齿频率与有关叶片加减轴转速的边带频率来说，由于指示了连接的问题通常是很重要的。

（4）应用正弦波作声波分析声的传播机理是一系列压力波的传播。当噪声形成一音调时，大气压力刚巧超过源的表面而有某些增加。这一高压波经过空气送达听者。

该高压空气的小的冲击作为声波作用于听者的耳朵。两高压脉冲之间存在着比大气压低的空气区。所以，如果在听者耳朵处作时间-压力曲线，该曲线类似于正弦曲线。如果声源产生的是单一的音调，它将是纯正的正弦曲线，这就使得用正弦波描述噪声的传输是有意义的。同理，正弦波也可用来讨论振动现象。声波是用扬声器测量的，它实为对小压力灵敏的压力传感器。声波的描述必须用频率与幅度。声波幅度测量的标准单位为dB。

（5）基本问题的诊断旋转机械的每一活动部件都会发出它独有的振动信号。例如，轴承引起的一组频率不同于被连接器、齿轮、叶轮或失去平衡部件形成的频率。在适当的位置搜集有问题机器的总的振动信号，并将这一信息分解为频率成分，它能查明每一机器部件的效应。下面讨论适合在适当位置搜集数据，诊断某几类问题的几种简单方法，以及用单通道快速傅里叶变换频谱分析问题的诊断方法。(www.xing528.com)

任何旋转机械与其他机械有很多相同的振动特性，记住这一点是很重要的，这在无论机器是3Hz（180r/min）的水泵或167Hz（10000r/min）的汽轮机都是正确的。

（6）在何处测量振动对旋转机械振动读数通常取于系统中每一轴承座的水平、垂直与轴向取向，如图3.3-25所示。由于旋转器件的振动是通过轴承传输的，这一信息对有问题机器的制造厂是有用的。这一效应滚动轴承比滑动轴承更明显。进一步的振动读数可取自任何与已有的特殊问题有关的位置。

图3.3-25 通常对振动测量的设置

振动读数应采用垂直于感兴趣表面的换能器读取。对包含有高频的振动信号的获取，必须用以螺钉或胶紧固于被测表面的加速度计。这是因为采用手持压力不足以使加速度计紧贴表面正确地随高频运动。用加速度计磁耦合比手持读数更可取，但是对高频响应不如固定耦合来得好。

（7）故障查找下述导则是用来指导以简单设备与逻辑分析技术在开始接触问题时帮助作振动分析的。如果它的作用不能产生满意的结果，则应作具体的谱分析。优秀的无损检测工作者不做比实际需要更繁杂的工作。

1）背景读数。在假定机器振动超标以前，通常需要在某一特定位置读取读数以确定是否有可疑的设备正在运行。振动可能是由其他机械的振动通过管道或地面传输引起的。读取数据好的位置是在轴承、连接管道和可疑机器的底板上。读数的读取是当工场其余的设备正在运作时，以可疑机器运作时的读数与其不运作时的读数相比。

如果可疑机器的运作并不显著地影响未过滤的振动能级，可用一加速度计和一磁铁沿管道和地面“侦察”直到发现制造振动的“真凶”。如果有两个通道分析仪，可以完成相干校正，定位任何所关心的特定频率成分的源。

可疑机器是否是真正的“凶手”，另一确定的方法是停止工场全部其他机械运作，检测这台可疑的机器。这种最典型的检查最好在夜间或周末进行。

2）管道。记住，可疑的机器的质量常常高于连接它的管道的质量。问题很可能是由管道造成的而不是机器造成的，具代表性的，如由于未对准或者共振引起的与管道有关的问题等。当机器运行时，若管道能脱去连接的话，这是一个简单可行的方法。此时，倘若未经滤波的振动能级发生了变化（大了或者小了）下述问题之一可能存在：

①管道支持不合适，并形成了管道未对准，或者是驱动-被驱动机器-地基-管道系统自然频率偏移，以致造成系统内某些力的机制的激励，一个可能的解决方法是用柔性管连接以改变系统的刚度；②管道引起的机器内部失准（如轴承座的偏离等）。在这种情况下，必须改用柔软管连接。还必须注意管道内的热膨胀效应；③某些其他机器连接到管道，产生摇振本机器的问题，读取背景读数或以频谱分析仪试验平均同步时间；④某些流体条件，如水冲击、涡旋流或气涡激励机器等。必须沿管道移动加速度计以确定最大激励点。操作者寻找小孔或部分地关闭阀门。如果流体问题不明显，如通常那样，可用两通道分析仪校核管道的自然频率，查看是否共振激励。工艺工程师可以做出结论，确定恶劣的流体条件该如何处理。

3）基座与支架。不合适的基座和基座的支架常常形成机器振动问题。检查有关不良的安装，可在机器轴承处读取数据并与同一方向上机器安装脚处和靠近脚的基座上读取的数据相比较。如果安装脚处的能级明显高于靠近脚的基座的能级，则判定机器是没有合适地安装在基座上，必须扭转紧固螺栓并重新检查振动。

如果基座上的振动读数，靠近机器脚处的明显高于基座上其他地方的读数，则基座不够牢固。这通常出现于宽缘工字钢制的底座。这是由于它的关于垂直轴的抗弯力只是关于水平轴的抗弯力约10%的缘故。

可以在工字钢的边缘加固使其成为矩形截面的钢梁，它们能用来代替矩形截面的钢材；或者是在基座上加焊斜支撑或“×”形加强筋以增加其抗扭转刚度。所有的焊缝在强度上必须是连续的，而所有加强筋必须紧固至工字钢的腹板与边缘，如图3.3-26所示。工字钢基座不能以填充水泥浆加固。水泥浆看起来能解决弱基座的问题，但高频振动大约在3年内能粉化水泥-钢界面。原有的基座低强度会再次显现，但由于底座被水泥充填过，就不能再作焊接处理了。

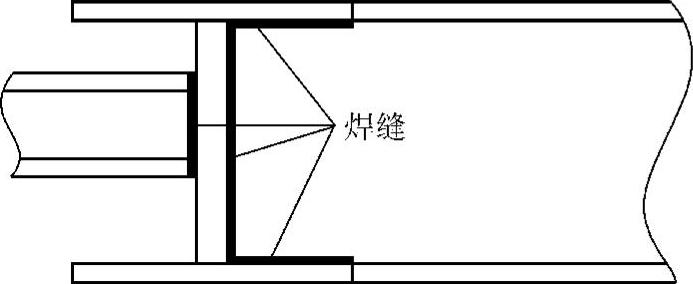
图3.3-26 正确（右）与不正确（左） 的工字钢加强筋的焊接方法

不良基座的另一信号是高能级的不准直连接信号的出现。此时，最好是立即对系统进行即刻准直。

有时过量的振动产生于劣质的基座支架。检测这一点，可以在感兴趣的机器上测量振动的同时拧紧与放松基座固定螺栓。在进行这种类型的试验以前，必须充分评估试验运行的安全性。

如果安装于地面的基座上的振动读数，比靠近固定螺栓的水泥或钢地面内的未滤波振动高1.5～2.0倍，则是基座未合适填隙、灌浆或安装至地面。很多基座为了稳定，要求良好的地面支撑。这类基座称为“非独立支撑”。

基座若是由于不合适的填充或灌浆引起削弱的，在一些时候可以采用具有将机器牵引至地面效应的永久变形（终凝）措施。在这种情况下，准直就不可能保持。已经观察到，在机器轴承上读取的振动能级，当基座固定螺栓放松时确实已经下降。这是由于基座已经打开清理改正。如果再填充、再灌浆仍不能解除问题，就要求更换一个新的独立支架了。

4）电的干扰。电气造成的问题，当供给电源断开时会立即消失。机械振动问题将随着机器逐渐减速至停止，在振动能级和频率上是慢慢减少至消失的。因此，一个电气的问题，可以通过在机器电源关断时注视频率中50Hz和100Hz的成分来辨别，如果是电的问题，能级会立即下降。电的干扰可能是不会影响绝缘的加速度计的小的接地回路或者是跨于机器轴承之间的几百伏的电压（形成轴承环的刻蚀）。一个简单的电压表可以检查这一问题。

5）柔性连接。在几种不同连接设计中提出了另一种连接问题指示仪。这类指示仪在频率等于连接销、齿轮或栅条数乘以每秒转数时为低能尖峰脉冲。这些频率给出了很早的初期连接损坏和不应忽略的事先警报。要注意的是，这些能级是很低的，除非用对数坐标检测频谱，否则就会消失。通常，这一受迫振动频率的预示在连接失效几个月之前就能出现。

一个松动的连接很可能产生关于频率的边带，如系统的叶片频率和啮合频率等。这是由于松动的连接不能驱动机器以均匀的速度旋转，而是按轴转速的倍数脉动。因此，信号以叶片转速和±n×轴转速（n为整数倍，如1、2、3…）相等空间边界清晰界定的，通常意味着连接松动（不是来自轴的不良装配就是来自连接部件的磨损），如图3.3-27所示。

（8）单通道谱分析一个典型的机组是由电动机或涡轮机组成的，设计一个或更多的连接以及被驱动的旋转机械以完成某些任务，诸如驱动水泵运送液体等。通常用齿轮箱、液压传动或带传动驱动泵作不同转速的旋转运动。所有这几台机器均具有机器内不同的机械部件形成的各自某一特定的振动特征。下面将讨论如何从快速傅里叶频谱分析仪观察振动频谱（振幅与频率的关系曲线），并由此确定在系统内，哪台机器的哪一零件产生了运作的问题。做这一工作，必须了解受迫振动频率的概念。

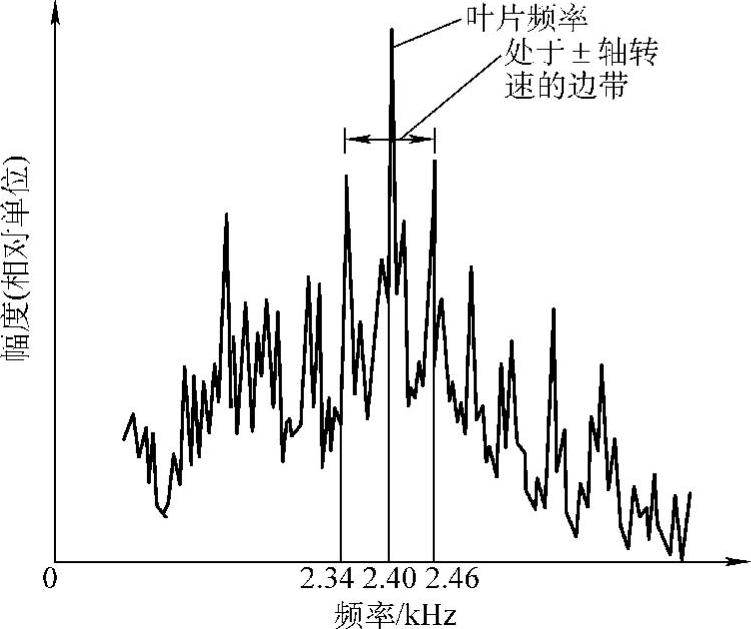
图3.3-27 关于叶片频率的边带

一台运行中的旋转机械在完成旋转一周的时间内，从轴上可能拾取了几个不同种类的事件。这些事件具有其必然存在于轴的每一转内的性质，就其本质而言，它们决定于机器设计的特性和计划中机器所要完成的任务，或机器的制造工艺。人们可以计算这些频率并在机器振动信号事件中寻找这些频率。一旦找到了这些频率，问题就集中在评估这些频率达到的能级是太高还是正常的了，人们必须首先定位受迫振动频率。

下述是从很多旋转机械中寻找出某些来自部件频率的方法。还有其他频率可能出现在一些特殊的设备中，懂得了下述每一种频率存在原理的分析者，对机理的分析具有了很好物理概念上的理解，就不难举一反三，很快掌握胜任于其他任何机械产生受迫振动频率的机制分析和计算方法。

图3.3-28 不平衡力=mdω²

1）旋转速率。每当机器运转时，总是要寻找系统中存在于每一旋转质量的旋转速率（即每秒转数）的频率信号。在旋转频率中出现峰值的成因通常是不平衡。由机器旋转质量误差产生的不平衡力是与不平衡形成的轴的重力中心与轴的几何中心的偏移量及转速的平方成正比，如图3.3-28所示。

因此，一台机器在某一转速具有的可接收的振动水平，而在较高速度则成为严格的水平。注意，不平衡力点径向地脱离质量中心而旋转则是与质量同步的。如果拾振器安装于机器的轴承上，比方说，在垂直方向，当旋转不平衡矢量直接指向拾振器的瞬间，拾振器的输出为峰值。如果这一峰值与其他同步事件的出现存在着相位差，例如一个键槽通过键相位的指示相图或者用频闪灯点燃照射一给定位置的键使之形成“同步事件”，测量其间相位差，就使得推断（辅以配重试验）重心位置和大小容易得多。然后，在离重心180°处加上适当的质量就能合适地平衡旋转质量。试图在任何一给定的转速下完全平衡转动质量是不实际的。将转子简单地平衡到使其形成的振动水平不足以损害机器即可。

另外一些常见的产生以轴转速为频率的信号是连接失准、轴的弯曲、传动带或齿轮驱动的偏心或不平衡。这可以通过观察整个机器的相位差或相对于系统几何形状的最高振动水准的方向，从可能造成轴转速频率信号的众多原因中加以区分。例如，轴的弯曲，机器两端轴承由于受弯曲轴的力互相分离，在该两轴承套上形成相互180°的异相，如图3.3-29所示。

图3.3-29 弯曲轴

如果来自传动带或齿轮的偏心的不均匀的负载，在其拉力的方向将形成一个极大值。这一矢量是不转动的。振动水平随负载变化，并非必然随转速而变。

柔性连接形成几个不同的可能受迫振动频率。正如上面已提到的，不对准能显示出以轴转速为频率的信号。人们可以预期到这点，由于失准不可能形成高的连接不平衡力。典型的连接不平衡指示标志是2倍轴转速频率信号，常以轴向为最高。连接不对准在整个连接中具有近180°的相位差（主要在轴向）。

2）叶片频率。旋转叶片每次输送流体的通过近似于不连续的，例如用蜗壳挡板的，人们可以预期其所加的为冲击力。因此，若以6叶片泵转子为例，将有叶片频率等于6倍转子的轴转速。由于存在着腔室表面或冲击的成倍数的不连续，所以也可能出现叶片频率整数倍的频率。振动不再是纯正弦波的，波形将是由多项傅里叶级数所组成。人们应该要求查看一台工作着的泵、压缩机、风扇或涡轮机的叶片频率。无论如何，在该频率若有极高的振幅水平，例如一台水泵，就可能意味着泵叶尖与蜗壳挡板之间没有足够的间隙或者是泵已失速。任何旋转叶片机器，叶片频率的不正常高振幅都指示有关机器叶片流体的流径有问题。

3）齿轮。齿轮产生等于齿轮的齿数乘以驱动它的轴的转速的啮合频率。注意，大齿轮齿数乘以轴转速的啮合频率等于小齿轮齿数乘以轴转速的啮合频率，在图3.3-23中，齿轮啮合频率=100×（1800/60）=300×（600/60）=3kHz。

倘若取两齿轮以1.00比1.00相互啮合，并转动其中一个360°，则另一个可能转动359.99°或360.01°。这一行程的角度误差称为齿形误差，它来源于齿轮滚铣时的旋转角度误差。一组优质齿轮和一组相对廉价的齿轮之间的主要差别即在于齿轮加工的公差。

在啮合频率的高振动水平典型的形成原因是由于差的机械加工引起齿形误差、啮合面的磨损、不合适的齿隙或者任何会造成啮合齿外形偏离理想几何形状的其他问题。因此，对卸载的齿轮，由于齿误差被合适的油膜变化所掩盖，可能完全不会显示任何啮合频率。当齿轮开始加载时，油膜不再对误差起补偿作用，典型的啮合频率图形就会出现。

啮合频率边带的存在是与任何作为调制旋转运动的其他边带产生的原理相同的。在齿轮驱动的工况下，调制来自相遇两齿失灵引起的相互冲击。例如，假定有两个齿轮，每个以60r/min（折合1Hz）旋转的啮合齿轮，每对齿应在前两个已相遇齿恰好是0.01s后相遇，倘若其中一个齿轮相邻两齿间间隙过大，另一齿轮上的啮合齿不得不对冲击进行等待，造成齿轮减速。为了维持每0.01s一次的平均冲击率，下一对齿间的空隙存在时间比正常要略短，这就形成相遇齿的加速度。

齿轮组产生许多啮合频率的可能边带。啮合频率的边带加或减小齿轮转速的整数倍和啮合频率的边带加或减大齿轮转速的整数倍一般是由像偏心齿轮或不平行轴所形成的，它们使得一个齿轮的旋转“调制”了另一个齿轮的转速。由于振动是幅度调制和频率调制两者的组合，关于啮合频率边带形成的图形一般是在两齿轮旋转速率整数倍的一组不对称的尖峰。

啮合频率的高振动幅度与边带内的高能量成分，由于它们指示的是齿轮中两个可能存在的问题（见表3.3-14），通常必须加以区分。在啮合频率的高能级可能指示，例如齿形误差问题引起的两相遇轮齿的干涉配合等；而许多高能级边带可能指示不平行轴（由于过大的轴的偏移、两轴失准、齿轮轮齿或箱开裂），一个偏心齿轮或其他形式的调制运动。

表3.3-14 诊断齿轮问题

推荐用具有频率扩展（图像放大）功能的频谱分析仪检查齿轮信号。下述齿轮的例子显示了扩展的必要性。

假若用一运转于60Hz，40齿的齿轮驱动300齿的齿轮以8Hz转动。可得到下述各值：啮合频率=40×60Hz=300×8Hz=2400Hz；在±n×60Hz的边带=±60Hz、±120Hz、±180Hz……在±n×8Hz边带=±8Hz、±16Hz、±24Hz……

为了观察啮合频率，分析仪必须置于5kHz档。在这一档，400线分析仪的带宽为β=（5000/400）Hz=12.5Hz。人们不能用一组12.5Hz宽的滤波器分辨8Hz间隔的带宽区间。要求用500Hz的窗口，已扩展的频率将为β=（500/400）Hz=1.25Hz。因此，用频率扩展方案检测大齿轮的边带并精确地确定齿轮问题是可行的。

仍然有较多的受迫振动频率可能由齿轮产生。一个是摇摆齿频率。在该频率，一个齿轮上的带大的几何不连续的齿冲击另一齿轮上带大的不连续的齿。如果齿轮组具有1.00：1.00的比例，摆动齿频率将与转速频率重合。然而，假定齿轮组具有100：101的比例，坏齿将只在慢轴的每101转时冲击。如果您在大的慢转速齿轮上听到偶尔每几分钟一次的“砰”声，这可能就是摆动齿频率。齿轮还可能产生寄生频率，它是由制造齿轮的工艺产生的，如果齿轮坯料加工时是夹在三爪夹头内的，而操作者过度夹紧夹头，齿轮的齿将被切割在一个不均匀的直径上，而当去掉时夹头，在三个对称的夹持处应力恢复形成“三角齿轮”，这就可能在3×转速处形成大的分量。其他制造齿轮的不完善可能产生其他寄生频率。

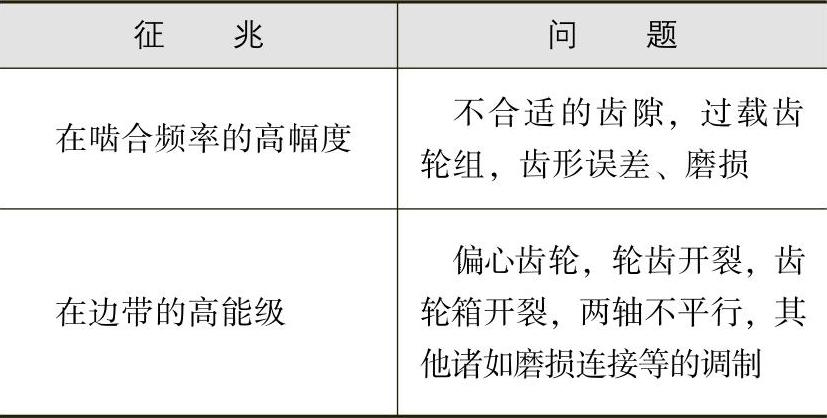
4）滚动轴承滚动轴承的滚动元件形成的几个频率是可以计算的。下述各式指出了由于轴承环不连续、滚珠不连续、隔圈不平衡形成的频率计算：

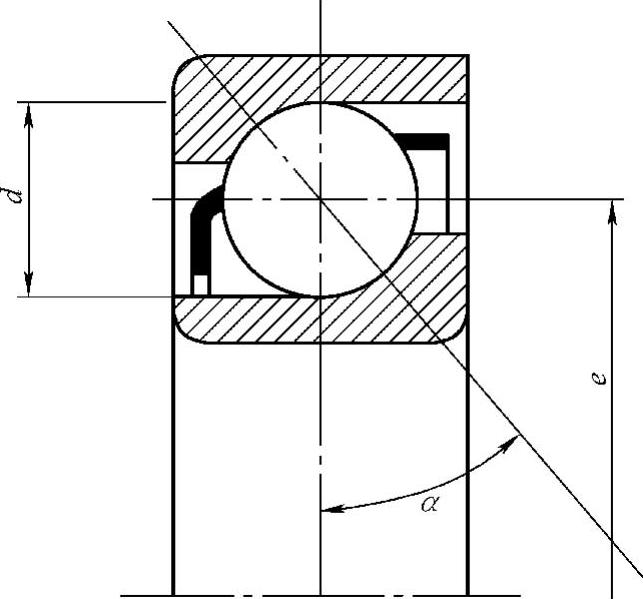
图3.3-30 轴承的几何结构

α—接触角（°） d—滚珠直径，单位为mm e—轴承中径，单位为mm

式中 f——旋转速度，Hz；

d——滚珠直径，mm；

e——轴承中径，mm；

α——接触角，（°）；

z——滚珠个数，如图3.3-30所示。

这些频率并不是总是很明显的。直到轴承正在进入它的损坏期以前，轴承与旋转机械其他部分相比往往是趋向于低能的装置：上述公式可能有用，也可能无用。

除非轴承负载方向与加速度计方向一致，否则检得内环损坏的几率是小的。任何内环与滚动元件间的冲击力的传输必须跨越过滚动元件，通过油膜，穿过外环并穿过轴承座到达加速度计。传输路径的难易，说明了外环的破坏是最易于观察到的。

滚珠轴承内滚珠的碎片常常并不与内环或外环相接触，这是因为某些时候碎片可能取的是轴向位置而没有打中轴承环。所以，这种响应很可能难于检得。

轴承振动监测的某些文献指出，轴承由滚珠问题造成损坏的可能最小。然而，更确切地说，可能是直到两环上出现像滚珠一样相当严重的损伤，滚珠损伤是最难探测到的。这一探测上的难题在滚珠轴承中并不明显，这可能是由于滚珠常维持在相对于环的同一取向。一直到轴承隔圈损坏到相当程度，才形成在加速度计处可以测量的不平衡量，这时离全部破坏可能已是为期不远了。

注意，轴承在套内的松动将会以约一半的轴转速自转，造成在这一频率出现尖峰。由于这个时候机器内部结构已不再适配，同时还可以观察到2倍转速频率的尖峰。

在轴承分析中更为令人困扰的问题是，当轴承元件在油膜内相互滑动而不是维持滚动接触时，是上述公式所未能估计到的。虽然滑动时间通常会只百分之几，但已经观察到在汽轮发动机的某些运作模态过程中几乎达50%。

还有其他几种技术可用来确定轴承的工况。一种方法是观察所使用的加速度计的自然频率。轴承内的缺陷（不完整）在频域内表现为具有短持续脉冲（近似于冲击脉冲）性质的白噪声。也是由于白噪声包含所有频率也包含等于加速度计自然频率的频率。

因而轴承内的缺陷会激励加速度计的自然频率。由于白噪声在加速度计共振点的放大作用，该激振脉冲将起到轴承损坏早期指示器作用。加速度计往往具有30～90kHz范围内的共振频率。因此，备有一台具100kHz范围频谱分析仪对这一激振脉冲技术是必要的。市售有测量这一现象存在的专用装置。

如果频谱分析仪可建立频率扩展功能，就能以足够的分辨力查找加速度计的自然频率，用以观察以上述公式计算的各种轴承频率处的边带。必须注意的是，这一方法只有在加速度计安装在轴承上的牢固状态足以传输高频脉冲（加速度计必须直接用螺栓固定在轴承套上）的工况方能实施。还要提醒的是，某些加速度计为了扩展工作范围，用高通滤波器以减低其共振效应。这类加速度计不能用来显示激振脉冲读数。

上述方法的另一种变型是确定尖峰脉冲曲线下的能量面积。这一测量获得的数值像频谱分析方法或激振脉冲方法一样，是正比于表面损伤的区域而不是深度。在损坏开始阶段以后，损伤面积增加多于损伤深度增加。

任何依赖于产生白噪声以定位轴承问题的技术存在的一个重要难题是，系统内可能存在其他白噪声源。典型的例子是蒸汽泄漏，无论是谁试图在造纸厂的干燥机轴承上检查其轴承工况，必然会发现所有轴承均出现了麻烦。这是因为所有轴承往往都是靠近来自干燥机的蒸汽泄漏。激振脉冲计不能区分是来自蒸汽泄漏的白噪声，还是轴承损坏的白噪声。这种情况下的应用，唯一有机会选择的是应用上述计算受迫振动频率公式的频谱分析。

再有一个监视轴承的方法是永久性地安装一个上限频率为10kHz着陆高度表以检测轴承外环的微小运动。一般认为，故障的冲击是足以使外环作能被测得的运动的。

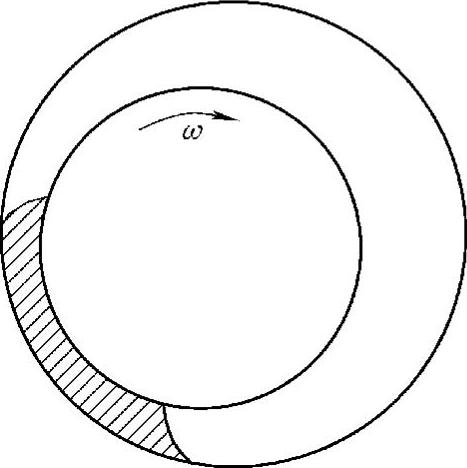
图3.3-31 滑动轴承的油楔

5）液膜滑动轴承。机器在运转过程中，轴的圆心不再保持在液膜轴承的中心，这是由于相对来说大的轴承间隙和厚的支持轴的油膜楔形浇口厚度形成的。这就使得，当各种不稳定在油膜内形成时，轴就可能在轴承内产生旋涡。这些旋涡频率范围为轴转速ω的30%～50%，并指示了油膜稳定问题，如图3.3-31所示。

这一不稳定性还可以从轴轨道轨迹形似“8”字的图形看出，它可以来自轴承磨损形成的过大间隙，也可能来自由不合适的压力、温度或润滑条件造成的油的粘度不当。如果问题是由设计不当，而不是磨损造成的，这里有几种解决方法：①通过收紧间隙使油膜楔形浇口负载加重；②增加轴承表面单位表面面积上的负载；③用倾斜的垫片或④用轴向开槽轴承分解浇口的层流特征。

监视油膜滑动轴承时，明智的措施是通过将油的样品送铁粉记录仪校核，在有规范的基础上周期性地检测油的工况。滚动轴承往往有一个逐渐相对恶化的过程；而油膜滑动轴承常常几乎是突然损坏，用加速度计和温度传感器连续监视要害机器是不错的主意。

6）气涡现象。气涡现象是由液体流动区域内，液体的局部压力下降至汽化压力以下形成的气泡内爆所造成的。内爆是在液体的压力增加到超过可以维持气泡存在的压力时发生的。内爆会在靠近其爆裂处的金属表面撕下微小的薄片。

由于气泡崩坍是一高能量、低持续时间事件，因此可以用检测轴承损坏的同一方法检测（用加速度计的谐振频率），或者用注意跨越整个注意的频率范围内能级的突然增加。这一增加将是低能的成分，因此频谱的峰值可能不变，但谷部将趋于被填充。

7）松动与摩擦。螺栓松动地在其孔内运动，而不是呈现前、后摇摆的光滑的正弦运动，将会被孔壁削去螺纹的顶端。该运动在某种程度上类似于方波或梯形波。信号具有激励频率（通常为轴转速）的很多谱波。螺栓冲击孔壁还可能加白噪声于该频谱，并在系统内分离出任何自然频率。

摩擦可以被设为是一个干摩擦旋涡，摩擦所形成的频谱，可能在下式的频率有尖峰

一个轴的轨道曲线图会显示出一系列环的首尾相接形成一个圆。轨道的方向与轴转动方向相反。要注意的是，轴摩擦可能形成足够的局部发热使轴弯曲，引起上述的不平衡与失准信号。摩擦还可能产生白噪声显示自然频率。

8）电动机。电动机利用的是电磁力和机械力，因而具有某些有别于液压动力或纯力学的旋转机械的特征。例如，电动机的轴可能由于来自叠层短路堆积的局部过热形成弯曲。这种现象所显示的是与上述旋转速度下的不平衡是相似的，但是平衡显然不是解决这一问题的对症方法。

还需要指出，纯力学的机械在研究自然频率时，可以模拟为一组弹簧-质量系统，电动机还有“电磁弹簧”性质，它是负载、间隙与磁化中心的函数。

在电动机定子内的不连续可以看成为在两倍电源频率处的尖峰，这在我国通常为100Hz。假如注意观察快速傅里叶变换分析仪上的频谱，在瞬态或指数平均模式（用尽可能少的平均）上会显示出，当电动机电源关断时，在100Hz的电气问题将会立即消失；而机械的问题将随着旋转质量转速降落至停止，并变化其幅度与频率。

旋转的电的不连续，例如一个断路的汇流条，将显示具有边带频率

f_边带=每秒转数±2×滑动频率 （3.3-36）

滑动频率是电动机同步转速与其实际运转转速之差。在我国可能的同步转速即100被除以电动机的极数（Hz），对正常合适负载的感应电动机，滑动频率通常为转速的5%。

（9）小结实际生产中有远较这里有限描述的要多得多的可能受迫振动频率。但是倘若能对上述的各种机理加以理解，则类似的原因可以采用推理的方法应用在具有特性的机器上。

振动分析作为无损检测旋转机械元件的不连续是一项新的技术。在以上的讨论中把注意力集中在自然频率上。无论在一个特殊的受迫振动频率下的能级是不是高，它都是需要确定的。