单点激振单点测量优化策略

单点激振单点测量多用于棒、梁、轴、板簧等形状简单的工件。方法是测量其自然频率（与阻尼），以判定工件的完整性。

从下述最简单的构件的微分方程式可以得到构件弯曲刚度EI（E为材料的弹性模量、I为截面的二次矩）、单位长度质量m、剪切刚度K_s和旋转惯量ρI（ρ为材料密度）的改变所引起的自然频率f_i的变化，且EI、m、K_s和ρI的小的变化所引起的f_i的变化是近线性的

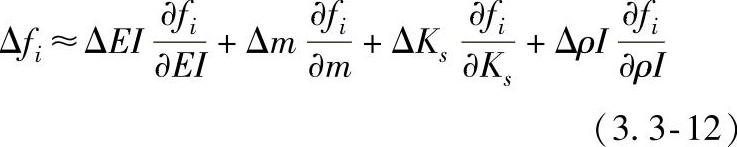
构件局部存在缺陷，以及尺寸或材料的差异会引起EI、m、K_s、ρI等参数的变化，从而引起频率的改变。而且根据各个局部缺陷引起频率变化的叠加，还可以作出对多重缺陷引起的综合的频率变化的估计。

自然频率对尺寸变化很敏感，若将这种方法用于制造阶段小裂纹的检测，则只限于尺寸公差要求很严格的构件。一些航空航天复合材料构件中的常见缺陷，如分层、脱粘、气孔等均可用这一方法检出。频率测量也可用来校核构件尺寸是否符合技术要求。

检测的基本方法是在构件的一端轻敲，从安装在构件的另一端的小型加速度计获取振动信息，并用快速傅里叶变换（FFT）分析仪分析其频率响应。

作频率测量时，为使构件所受的制约最小，被测构件的支点应在所选振动模态的两个节点（振动幅度最小）上。

最简单的情况为均匀棒的轴向振动，两端自由的棒产生基频（最低）振动模态的位移为

式中 u₀——长度l的棒在x=0处的周期位移。

这就确定了位移模态的形式。自然频率则为

f_i=αc/l （3.3-14）

式中 c——声速（m/s），c=（E/ρ）^1/2；

l——长度（m）；

E——弹性模量（Pa）；

ρ——密度（kg/m³）；

α——频率因数；

f_i——自然频率（Hz）。

有时，所关注的是周期性的应力或应变。

应变ε由ε=∂u/∂x确定，见式（3.3-15），而应力σ则由σ=Eε=E∂u/∂x确定（假定阻尼为零，所带来的误差在多数实用的情况下是可以接受的）。

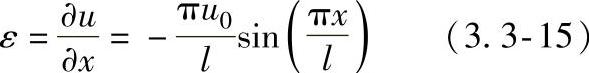
图3.3-1示出了两端自由的棒的轴向振动位移和应变模态的形式；图3.3-2示出了一端固定的棒轴向振动位移和应变模式；图3.3-3示出了两端固定的棒的轴向振动位移和应变模式。从图3.3-1～图3.3-3可以看出，应变模式与位移模式完全不同。还应注意的是运动同棒的轴平行，为了观察方便，图中示出的是垂直位移，节点处位移为零。

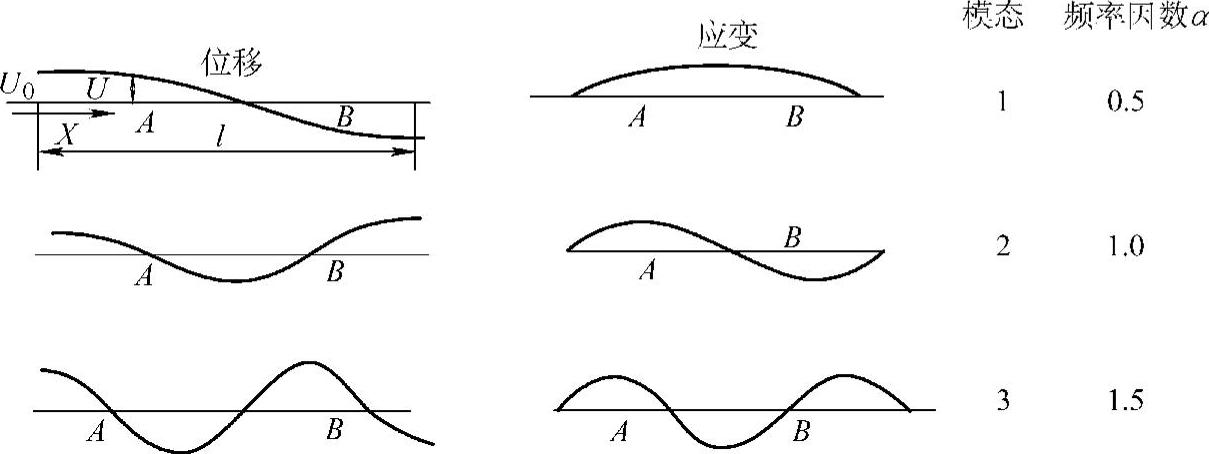
图3.3-1 两端自由的棒的轴向振动位移和应变（应力）模式

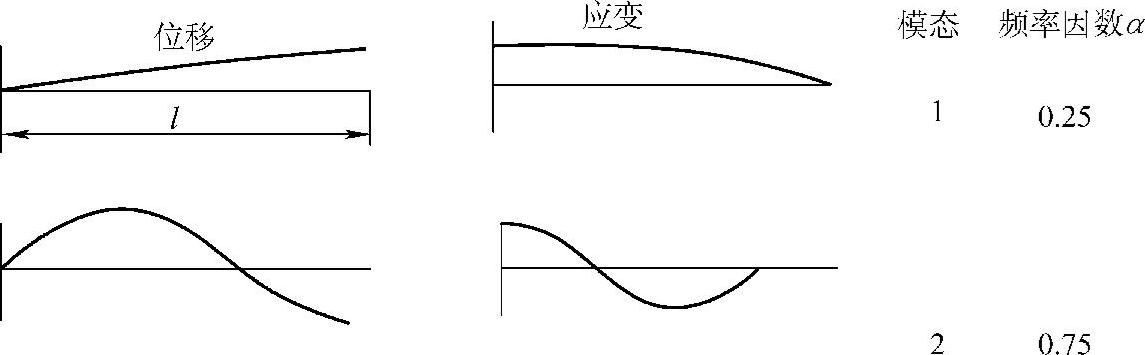
图3.3-2 一端自由的棒的轴向振动位移和应变（应力）模式

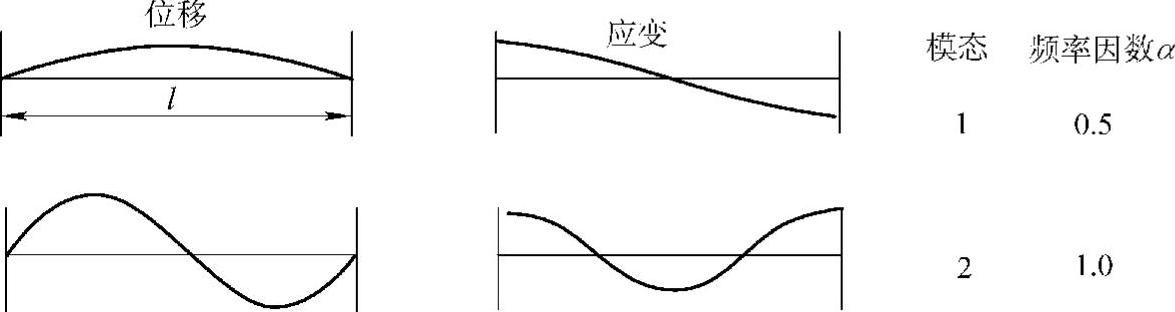
图3.3-3 两端固定的棒的轴向振动位移和应变（应力）模式

将各式中的E用剪切模量G来代替，相关各式还可以用于扭转振动。

通常所用的是弯曲振动，运动微分方程为

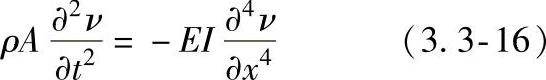(www.xing528.com)

式中 ν——垂直于构件平面的位移；

ρ——密度；

A——截面积；

E——弹性模量；

I——截面的二次矩。

其自然频率为

f_i=（α/l²）（EI/Aρ）^1/2 （3.3-17）

式中 l——长度；

E——弹性模量；

A——截面积；

I——截面的二次矩；

ρ——密度；

α——频率因数。

弯曲振动自由-自由与固定-自由（悬臂梁）的典型模式如图3.3-4和图3.3-5所示。航空发动机叶片所受的振动与图3.3-5固定-自由的条件很相似，通常可按此进行检测。

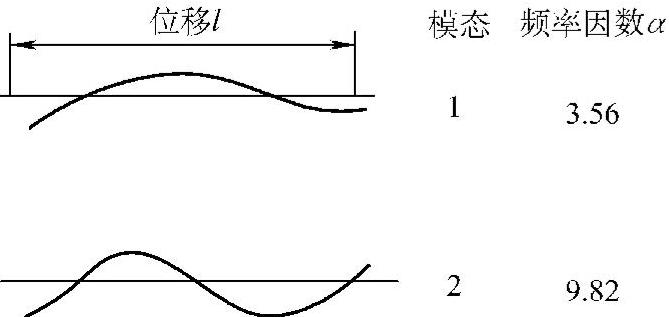
图3.3-4 两端自由的桁条弯曲振动模式

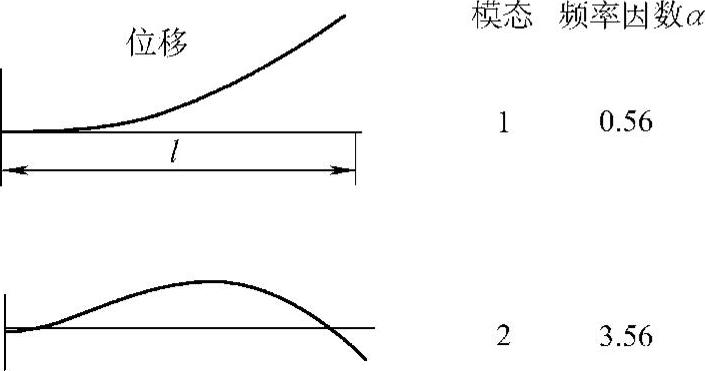
图3.3-5 一端固定的桁条弯曲振动模式

检测程序按下列步骤建立：

1）根据一批待测样件的自然频率和模态形式确定一组可供检测选用的振动模态。

2）选择其中几个清晰和容易测量的模态。

3）确定检测条件下对模态参数测量的灵敏度。

4）用瞬变过程测量，确定样件在这些模态下的自然频率并以此作为原始基准频率。

5）加工样件，制成实际构件中很可能出现的人工可控损伤。

6）在典型的良好控制条件下，再次检测有损伤的样件，测出其自然频率（即共振频率）。

7）比较每一样件损伤前、后的测量结果，确定足以引起明显频率变化的损伤类型和损伤程度。

8）用数据处理技术或图像识别方法，比较每一样件的原始数据与测得数据，评定用该项技术检测给定损伤的可行性。

9）选定缺陷的检测标准。

由于单点激振单点测量技术以某些正常（无损伤）的模态特性为检测依据，如果整批构件的允许误差能够达到很小，便可获得更好的检测效果。