如何监测材料各向异性？

复合材料在关键承力部位的应用，它们必须具有适于所要求无损地评定其损伤力学效应的能力。一种实用的方法是声-超声波或称之为应力波因子的方法。

就实际应用而言，该方法的一个优点是，只需从工件的一个表面取数。这种检测方法是把被检工件作为一个振动结构来处理，而不像常规超声波检测那样，作为单一超声波脉冲的简单传输介质。由于结构的整体性和粘接质量控制振动特性，关注这些振动特性是查找复合材料构件质量状况的一种有效方法（参见本篇第3章声振检测）。因此，声-超声波方法的研究，就是直接针对了解这些振动特性、力学性能与材料损伤之间的关系。

声-超声波方法一开始应用即涉及测量能量传输，如用测量接收信号高于阈值电压的电压尖峰（偏移幅度或振荡幅度）的数目（振铃计数）。先进的方法是采用模态波形表征能量传输。该方法的前提是相对于应力波（材料振动）能传输较多能量的材料，具有较高的质量。说得更明确些，比较容易传输应力波的材料比不能有效传输应力波的材料，就不那么容易使应力波集中而形成损伤。实际上，它已成功地应用于工件相对强度的预测，薄壁构件的损伤定位和疲劳样件的损伤监控。

应用模态波形表征检测得到的声-超声全波采样信号能提取更多的信息，对改进信号处理技术是有效的。数字信号分析领域的高度发展，提供了难以计数的算法可用来作声-超声波信号分析。例如，已经应用同态信号处理技术得出通过声-超声波方法在一块铝板内产生的特有的反射图形信息。又如，在本章2.4中专题介绍的小波变换算法。

声-超声波信号时间域与频率域信息的数字信号分析软件包已开发成功。简而言之，以下的讨论将集中在采用窄带分析和滤波程序计算定量参量（声-超声波参量）以表征声-超声波信号特性。

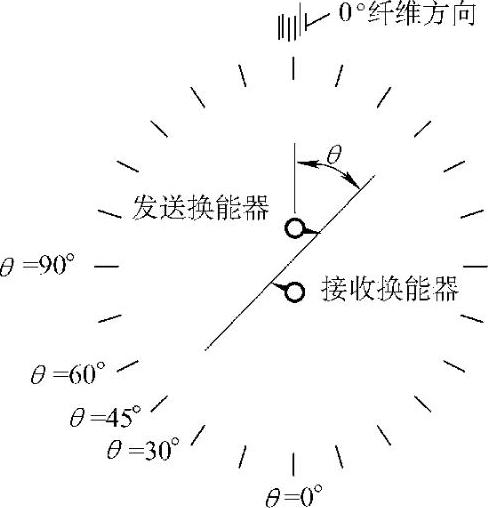
图3.2-17 方位角的定义

对于更完善地使用声-超声波方法是，用上述数据信号分析软件于一给定的复合材料板上分析以各种不同的方位角得到的信号（见图3.2-17）。检测时，两换能器沿中心旋转，并尽可能以小的角度逐点地变更方向，观察板材单点声-超声波参量的变化。从不同的方位角得到的每一个声-超声波信号计算出同一种声-超声波参量。其次，绘制出得到的声-超声波参量图，它示出了实际声-超声波参量作为方位角函数的变化。此后，即可用这些图形作为材料各向异性的指示了。换言之，材料的各向异性状态形成了不同方位角应力波传播的差异。随同方位角的应力波传播的变化形成了声-超声波信号的改变，从而导致了声-超声波参量的偏离。

1.物理意义

初始关心的机理是，如何使输入脉冲转换成为接收换能器的输出信号。实质上，它涉及工件转换一宽带脉冲为相对频带较窄的特定频率的振动，换言之，工件对输入脉冲的作用如同一个滤波器。最终，可以采用处理工件作为具有在其顶面与底面间应力-自由边界条件的波导，并考虑在什么频率下能使工件厚度与波长的整数倍相关联，引起相长干涉来解释这种现象。另外，必须考虑到可以在两表面间传播的波的不同类型，以及可能被激励的表面波。

对各向异性材料板波问题的完整形式，使得有可能对这一表达式作具体分析。Pao和Kaul还讨论了各向异性材料中板波更加普遍的问题的解。首先，解中包含有对材料中通常的体波求解。其次，考虑在顶与底的两表面上的无应力边界条件，并假定对于中间板的对称或者是非对称特性，联系体波解的叠加，求出板波解。对波长大于板厚的波，声波是作为基频板波传输的。该问题的解的求出可用叠层分析方法。在波长小于板的厚度时，在体波与形成的板波按照板的厚度得出的截止频率之间存在着联系。这些截止频率可从下式求出

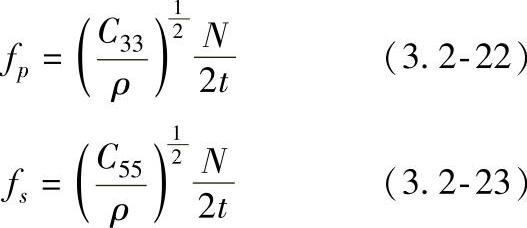
式中 ρ——质量密度；

t——板厚；

N——1，2，3，…；

C_ij——刚度矩阵（以比张量法表示）。

对称模式的截止频率由N为奇数的f_p和N为偶数的f_s给出；非对称模式的截止频率由N为奇数的f_s和N为偶数的f_p给出。

对各向异性材料，垂直于恒定相位平面的单位矢量并不总是对准能量流。实际上，能量线的矢量可用数学式表达为

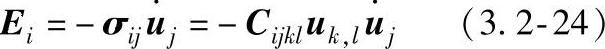
式中 ——时间导数；

σ_ij——应力张量；

C_ijkl——刚度矩阵。

工件的几何形状与力学性能两者通常对初始脉冲能量如何转为板的振动均有影响。另外，指示振动在不同方向各部分是如何分配的主因是工件的力学性能。虽然工件的不连续、不均匀和其他因素均会影响声-超声波的检测结果，上述介绍的简单的模型仍可作为解释试验结果的基础。

2.试验步骤

声-超声波方法当前的应用是，要求对复合材料表面给予机械激励以形成在工件材料内的机械扰动，同时在工件的同一表面（或另一表面）的另一位置用换能器感受由该扰动引起的振动。

监测复合材料板的材料各向异性，方法是置一发送换能器（5MHz）于板表面上的某一位置，并置接收换能器（5MHz）于同一表面相距25mm处。为得到所要求的随相位角变化的声-超声波信号（声-超声波参量）数据，必须有一个精心设计的试验程序。

在进行声-超声波测量以前，用一个准直夹具在待测板的顶面作标记以提供两换能器的合适定位。以与0°纤维方向（由叠层板的构成定义）平行的线作为待测板的0°线，并在围绕板中心150mm圆的圆周上以5°间隔画上短画线标志。然后，用一细棒通过准直夹具中心线而其端头与特定的相位角的两短画标志线准直，以保证换能器的相位角位置。

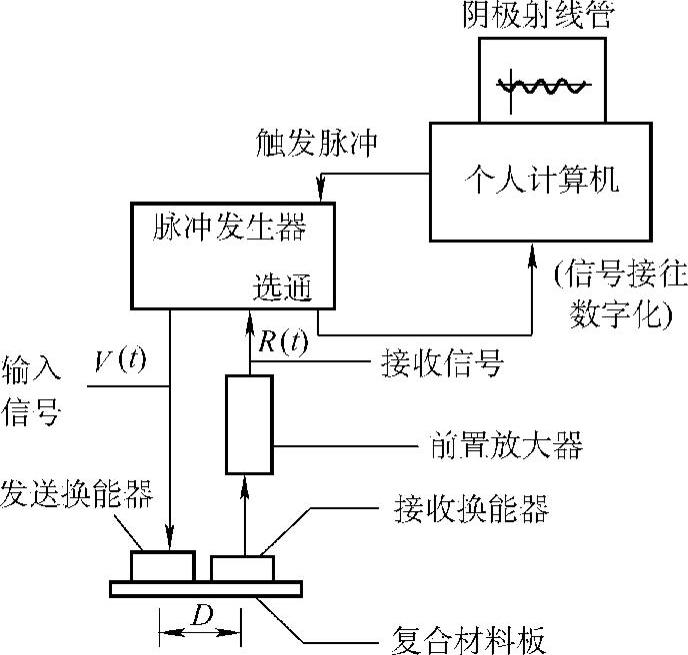
图3.2-18 试验配置

用图3.2-18所示的试验配置来获得测试结果。数据接收系统是用来进行仪器控制、信号获取与数据储存的。首先，数据接收板提供一触发脉冲给脉冲发生单元。接着，脉冲发生器送出一个300V幅值，0.6μs脉冲周期的电子脉冲至发送换能器。这样就在被测工件内产生应力波振动并被同一类型的接收换能器所感受且转换成电压信号。两换能器均以耦合剂耦合于材料表面。当两换能器实施测量时，均在它们的顶上置有100g的质量，以维持换能器的恒定接触压力。数据采集板上，接收到的信号在由模拟-数字转换器数字化以前，先经过前置放大器与脉冲接收单元上的阀门选通电路。模-数转换器是以送至脉冲发生器的同一触发脉冲触发以启动其数字化功能。通过键盘的控制，可以对多达128个接收信号平均以产生一个平均信号置于储存装置中。数据平均是用以减少来自电子放大器件的噪声效应的。置于储存装置中的数据组连续返回至阴极射线管（CRT）显示为电压-时间图。最后，数字信号信息存储于计算机中，用内部软件包作进一步分析。

实际上，试验数据是由上面描述的基本试验配置产生的。该试验配置如前所述，包含有用以获得发送换能器与接收换能器不同方位角取向的准直记号与夹具。因此，通过在给定的板上，从不同方位角得到的数据组的分析就可以得出结果。然后，用数字信号分析软件包即可计算出作为方位角函数的声-超声波参量并制出图形。试验结果是由下述石墨-环氧树脂复合材料得出的：

[0，0，0，0]；

[90，0，0，90]；

[0，0，0，0，0，0，0，0]；

带中间分层的[0，0，0，0]。

中间分层是在中间层之间镶嵌夹入物制成。发送与接收换能器的旋转是以分层的中心作为中心，两换能器始终跨立于分层之上，但从不直接置于分层上（即分层直径小于两换能器边距）。发送换能器与接收换能器的距离，在全部记录声-超声波参量过程中，中心与中心之间均保持在25mm。

计算机分析的初始步骤是从存储器检索数字信号开始的。接下来观察总的信号特征使生成电压-时间图形。附加的子程序提供对信号的选通，并从信号中消除任何直流偏压。再通过用波列到达（即第一个非零电压读数）的时间（例如从触发瞬时测量）除以两换能器的距离粗略地估计波形到达的速度。进而对某些情况，可用增加两换能器间的距离并注意波列中的一个特定的点在时间域中的变换以估计相速度。计算机屏上的时间信号内的峰值会随着接收换能器从发送换能器的离开而呈现同步偏移。对1MHz信号成分，当接收换能器在工件上移动时，信号的总的形状变化很小。因此，可以将该程序应用到与占优势的单一频率成分相结合的波列部分以确定与波运动特殊频率有关的波的速度。

用快速傅里叶算法对选通的数字电压-时间数据产生频率域信息。该电压-时间数据是从第一个非零电压读数至波列末端选通的。用快速傅里叶变换可产生幅度-频率与相位-频率数据，从而绘出幅度-频率曲线图形并计算出声-超声波参量。

声-超声波参量的测定涉及关于纵坐标的谱密度（幅度值的平方）的不同动量的计算，例如，倘若S（f）是谱密度函数，n次动量定义为

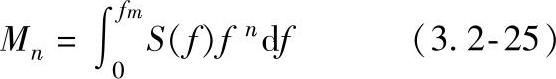
式中f_m——奈奎斯特（Nyquist）频率。

在数字数据的分析中，积分可以用相加代替为(www.xing528.com)

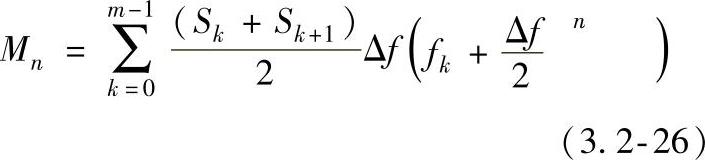
式中 f_k——相应频率值；

S_k——谱密度值；

Δf——f_k与f_k+1间的频率差。

例如，0次动量定义为

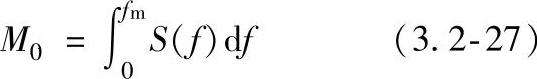
因此M₀是谱密度曲线下单纯的面积。这可以在分析上与电压信号的平均相关。由此可定义出声-超声波参量频率域参数

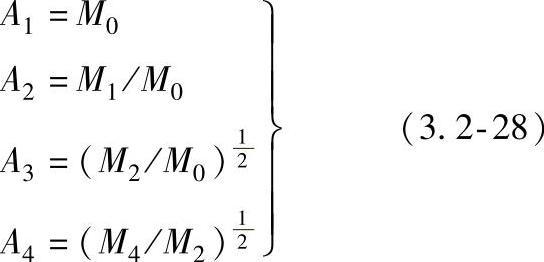
这里，定义A₁为M₀，是关于接收信号总能量的指示。定义A₂为M₁/M₂，而且是信号的中心频率。所以具有较高A₂值的信号与具有较低A₂值信号相比，表示能在较高的频率下（比在较低的频率下）成正比地传递更多能量。此外，定义A₄为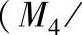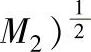，定义A₃为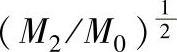。A₄是最高频率，而A₃是零电压跨越频率。A₄/A₃为失真系数，指示在一个主要为较低频率占优势的信号中，高频信号的分量。图3.2-19指出了动量与频谱密度函数的相关性。在另一方面必须注意的是，对给定的频率值，谱密度函数是幅度函数的平方。

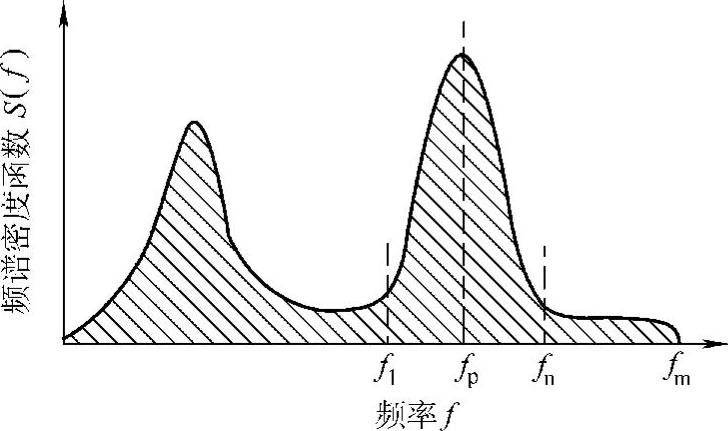
图3.2-19 滤波后A₁值的计算

为得到更专门的声-超声波方面的信息，在数字信号软件分析中包含有滤波功能。本质上，它所涉及的是特定频率范围M₀的计算。从而，可以得到谱密度曲线特定部分下的面积。数学上，它可表示为

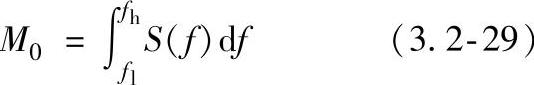
式中 f——频率；

S（f）——谱密度（幅度平方）的量值；

f_l——低频率端点；

f_h——高频率端点。

实际上，这一特征是用来查找在幅度-频率曲线中一个频率峰下的面积，产生一个参量用以指示特定振动频率范围内能量的传输量。试验一开始，观察幅度-频率曲线，揭示对给定板厚在相同频率某些幅度峰值的存在，而不考虑板的敷层或其方位角。然后，检查不同方位角的幅度-频率曲线，确定f_l和f_h值。接着，用所确定的f_l和f_h值计算从不同相位角得到的声-超声波信号的滤波动量值。经滤波声-超声波参量定义为：

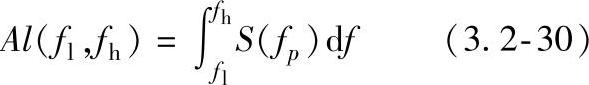
式中 f_p——最大频谱密度函数的频率；

f_l——所选滤波器的下限频率；

f_h——所选滤波器的上限频率；

3.试验结果

用时间域结果的观察与幅度-频率曲线所揭示的信息既可以对声-超声波方法作较具体的了解，并且可以用作计算和解释声-超声波参量的依据。

首先，检测结果意味着在幅度-频率曲线内呈现的峰值幅度处的频率是与板的厚度成反比。这是与结构-破坏波干涉模式相一致的，此处结构波的干涉最终将产生板厚为波长的几个整数倍的板波。它的一个重要的隐式是，复合材料可以精确地设置到局部区域作为结构的振动，从而使之与复合材料的振动特性（例如材料结构）在某种程度上的改变问题紧密相关联。

虽然，幅度-频率曲线通常还包含有其他峰值，但1.0MHz和3.4MHz两峰值（对4层叠层）始终为较高幅度（见图3.2-20）。确切地说，某些信号在300kHz范围显示较低频率的峰值，但幅度值是以随机方式变化的，而且在很多信号中不能辨认出为一个峰值。对这种效应的补偿工作是在软件包中采用一个转换因子进行计算。还应注意的是，在某些实例中，经常存在的幅度峰值之一具有一个或两个邻近的峰值（见图3.2-20中3.4MHz前后的峰值）。

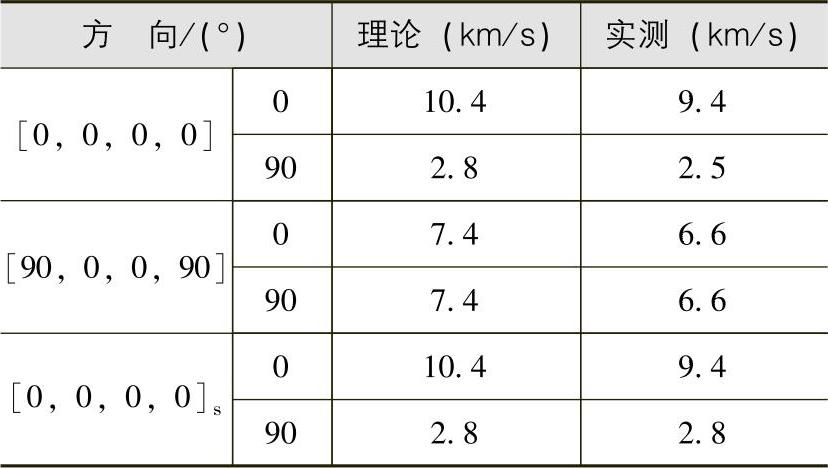
表3.2-3列出了对几个特殊点的波速估算值。首先，可看到的是4层和8层叠层的速度是相同的；次之，也是重要的是，在[90，0，0，90]的叠层，0°、90°方向速度相同。因此就显示出1MHz信号波的波速与弯曲刚度无关。这与1MHz信号成分是由对称兰姆波组成的提法是一致的。较高频率幅度峰值（对4层叠层，3.4MHz）就波速估计来说，显示一致的结果就要少一些。

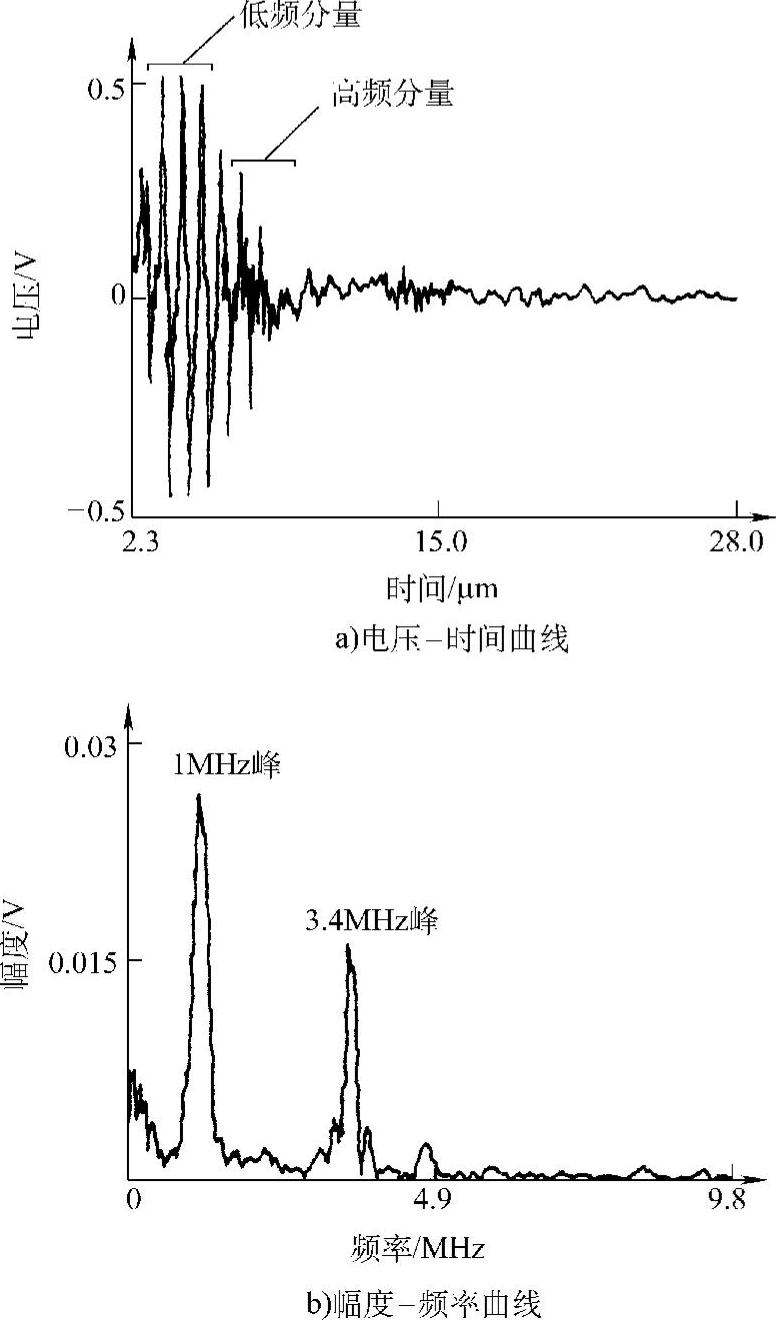
图3.2-20 [0，0，0，0]叠层板0°方向的检测结果

表3.2-3 一阶对称兰姆波波速理论值与实测值比较

试验曲线显示声-超声波参量随角度方向变化揭示了某些值得注意的趋向。首先，所有叠层，当方位角与叠层之一的纤维方向相同时，尤其是当与外层的纤维方向相同时，显示较高A₁。观察A₁（0.8，1.2）和A₁（3.2，3.6），由于它们相当于A₁值的主要组成，显示出具有类似的特征。然而，A₁（3.2，3.6）值所显示的随方位角离开纤维方向的变化，与A₁（0.8，1.2）的变化相比，始终以比较慢的速率相减少。这种特征类似于叠层随方位角的视在伸长模量E_X的变化。从而，A₁（0.8，1.2）随方位角的变化，很可能是以某种方式，主要是依据E_X随方位角的变化。就物理意义讲，这一特征似乎与信号的1MHz部分是对称的兰姆波是相一致的。

有几个因素关系着声-超声波方法实际检测的可靠运用。首先，关于围绕圆心的圆环上两换能器的位置，方法的结果受具有可变位置的发送-接收换能器在位置改变时，对所形成的接收信号变化的影响。因此，不论是发送换能器或者是接收换能器区域下，随着材料的变化都将使接收信号急剧地改变。

因此，特定方位角的测量并不总是能表征所要求的两换能器之间的材质。实际上，不连续位置相对于换能器布置之间的精确关系是一个正在不断研究的领域。在一个特定方位角的检测结果，可能与表面的不连续或位于发送换能器或接收换能器所处位置的其他不连续有关。就检测结果解释来说，这虽然带来了复杂性，但它仍然提供了有关工件材料不完整性的附加信息。

声-超声波方法的实际应用必须是自动实施执行的过程。特别是实现换能器与工件的耦合必须用交替补充法，用超声波耦合的方法对目前这一方法来说是不适宜的，耦合剂使用状况的某些变化将会影响检测结果。一种解决方法是采用特种形状的换能器，例如发送换能器可用质点冲击系统来代替，接收换能器可用激光干涉系统代替。还可以用单一源的以多个接收换能器阵列相围绕以代替旋转的一个接收和一个发送换能器。再者，对特殊的应用，所关注的参量是可以预先加以确定的，可以开发一个模拟分析系统与用户控制的数字数据分析程序相对应。

最后，由于检测结果看来是与结构共振有关的，被检工件上其他结构部件的抑制作用将会改变结果。所以，同一材料的工件，根据其在结构内的特定的位置以及所形成的边界抑制，可能产生不同的声-超声波数据。例如，检测一个复合结构，可能是有钢背衬表面的，也可能是具两自由面的。而边界条件的不同，可能会改变声-超声波检测的结果，也会影响在使用载荷下材料的响应。通常试图说明几何形状、边界条件和材料状态分别对声-超声波检测结果的影响，分析将变得相当困难。

大量的信息存在于声-超声波检测信号中，这就要求我们要适当地解释检测结果，必须善于运用其他信息。这就意味着每一次声-超声波检测方法的-实施，要求一定数量的分析与模型，因此要求有一种能例行于各种部件而不需要任何分析的纯属常规声-超声波方法是不现实的。另外，输入的与其他系统部件的频率范围必须在可以激励的共振范围以内，从而可据此优选系统，这通常是成功应用的依据。

4.结论

总的说来，检测结果显示了声-超声波信号中存在着大量信息。它们同时指出了声-超声波方法对面内各向异性是灵敏的。更确切地说，所出现的试验结果指出，对所关注的石墨-环氧材料，信号包含有两个主要振动频率，其中每一个均以不同的方式，以方位角为函数变化。上述的不同可以通过声-超声波参量与它们随方位角的改变进行定量。1.0MHz信号成分（4层0°叠层）看起来显示出对称兰姆波的某些特征，而且具有类似于明显叠层伸长模态方式的随方位角变化的能量成分。

材料性质、不同声-超声波参量与它们随方位角变化之间的关系，既形成了有助于给出声-超声波方法的物理基础，又引入了一种对面内各向异性灵敏的无损检测技术。各向异性既是复合材料力学性能中一个重要因素，又是受异常材料作用的一个特征。