小波变换方法优化：探索实用方法

从前面的分析可以得知声-超声波信号是瞬态非平稳时变信号。常用的波形分析，由于适用的是周期的平稳信号；频谱分析又是一种忽略局部信息变化的全局分析法，显然都是不适用的。再次傅里叶变换（SFT）和基于短时的傅里叶变换（STFT）的短时谱增强算法，从本质上讲都是一种单分辨率的信号分析方法。而非平稳信号，当信号在阶跃或脉冲突变点等处剧裂变化（信号的高频部分）时，要求有较高的时间分辨率；当信号变化平稳（信号的低频部分）时，要求有较高的频率分辨率。由于SFT和STFT使用的都是固定窗宽，无法同时兼顾上述两者，因而也很难获得较好的效果。

小波变换（wavelet transform）属于时间-频率分析方法，它具有多分辨率的特征。它在时域与频域都具有表征信号局部特征的能力，即在低频部分具有较高的频率分辨率和较低的时间分辨率；在高频部分具有较高的时间分辨率和较低的频率分辨率，很适合分析声-超声波检测中包含的瞬态异常变化信号，并能展示出其成分。

小波变换发展了传统的傅里叶变换算法，它在时域和频域都具有良好的局部化特性，特别是对非平稳时变信号的分析明显优于常规的傅里叶变换。

小波变换算法在语音分析等信号处理中的应用已较成熟。引入到无损检测领域，尤其是超声波、声发射和声-超声波检测中的应用，则自20世纪90年代开始。国内近10年来，以高等院校和研究机构为先导，也纷纷开展了这方面的研究工作，取得了可喜的成果。

现将小波变换的物理概念和算法简介于下。

设f（t）为任意平方可积函数（如有限能量的传输），可记为f（t）∈L²（R），ψ（t）为基本小波或母小波，ψ′（ω）为ψ（t）的傅里叶变换。设ψ（t）和ψ′（ω）均为带限的，并设这两个函数的中心和半径分别为t^∗、ω^∗和Δψ、Δψ′，则根据小波基函数ψ_a、b（t）的定义可确定它的时域窗为

[b+at^∗-aΔψ，b+at^∗+aΔψ] （3.2-7）

根据傅里叶变换的定义，ψ_a，b（t）的傅里叶变换为

则相应的小波基的频域窗为

小波变换对信号的分析可以理解为：通过变换平移因子b使小波窗口在整个时间轴上移动，对时域局部信号进行逐步分析；通过改变尺度因子a可在不同的频率区间，对时间窗内的局部时域信号进行分析。因此，小波变换也可理解为一系列的滤波函数，在不同的频率范围内对信号进行分析。

从而，f（t）的小波变换可定义为

式中 a——尺度因子；

b——平移因子。(https://www.xing528.com)

它的逆变换为

式中

ψ′（ω）为ψ（t）的傅里叶变换。

基本小波ψ（t）不是唯一的。当ψ′（ω）满足允许条件

则ψ（t）即为一个基本小波。

常用的基本小波（简称小波基）有：Hear小波、Morlet小波、Mexican Hat小波、Meyer小波、Daubechies小波系、Coiflets小波系、Symlets小波系。在工程应用中小波基的选择是十分重要的，用不同小波基分析同一信号会得出不同的结果。

可见，尺度因子a的作用是对基本小波ψ（t）作伸缩变化：a越大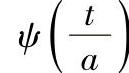，越宽，见式（3.2-7）。通过改变a，使小波变换具有多分辨率，即实施“在高频部分具有较高的时间分辨率和较低的频率分辨率；在低频部分具有较高的频率分辨率和较低的时间分辨率”的功能。

在计算机上实现小波变换时，必须选择足够多的尺度因子a值和平移因子b值才能体现出小波变换的时域-频域特性，这就大大增加了计算量。为了减少计算量通常采用二进制离散小波变换，即尺度因子a按2的幂级数离散化取值。此时，连续小波基函数转化为离散小波基函数，可记为

式中 τ——采样周期。

取a₀=2，则有

这里必须强调的是，离散二进制小波变换只是对尺度因子a进行离散化，而时域上的平移因子仍保持连续变化。因此，二进制小波变换具有“变焦距”功能，同时又不破坏信号在时域上的连续性，这一特征非常适合声-超声波检测的信号分析。