中子线衰减系数的计算及应用举例

中子射线照相的成像几何原理、衰减随材料厚度的变化、影响曝光的因素等均与X射线照相术相类似。但是，X射线与原子的轨道电子相互作用，其衰减与材料的密度和原子序数成正比；中子与原子中的轨道电子不相互作用，而与原子核相互作用，其衰减与材料的密度和中子截面成正比，与原子序数的关系则是随机的。

穿过试件的中子射线强度I与入射强度I₀的关系可表示为

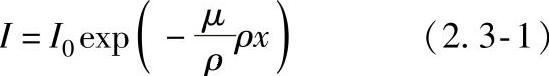
式中 μ——线衰减系数（cm^-1）；

ρ——密度；

x——穿透厚度。

而线衰减系数μ与中子截面积σ_t的关系可表示为

μ=Nσ_t=N（σ_a=σ_s）

式中 N——每cm³体积内的原子数；

σ_a——吸收截面，数值表2.3-1；

σ_s——散射截面，数值表2.3-1。

对于单一种元素的试件可写成

式中 μ——线衰减系数（cm^-1）；

ρ——材料密度（g/cm³）；

N_A——阿伏伽德罗常数（6.023×10²³/mol）；

A——单质摩尔质量（g/mol）；

σ——中子截面积（cm²）。

对于含多种元素或由化合物组成的试件，则其线衰减系数可由下式计算

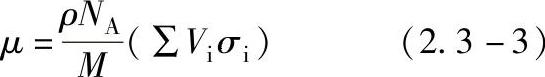
式中 M——化合物的摩尔质量（g/mol）；(www.xing528.com)

V_i——化合物分子中第i种原子的数目；

σ_i——该种原子的中子截面积。

作为实例，化合物聚乙烯（CH₂）的中子线衰减系数可计算为：

式中，ρ=0.91g/cm³；

N_A=6.023×10²³/mol；

M=14.0268g/mol；

V_C=1；

V_H=2；

σ_C=（4.74+0.0035）×10^-24cm²=4.744×10^-24cm²；

σ_H=（20.49+0.333）×10^-24cm²=20.823×10^-24cm²；

图2.3-1给出了质量吸收系数（线衰减系数/密度）与原子序数的关系，而在表2.3-1中则列出了某些元素由平均散射截面和吸收截面而获得的热中子线衰减系数。很多材料，如金属，强烈吸收X射线，中子能很容易通过。重元素，如铅、铀、铁和铋就吸收X射线而对中子的通过阻碍甚少；反之，轻元素，如氢和锂就强烈吸收中子，而X射线却能自由通过。

图2.3-1 质量衰减系数（线衰减系数/密度，μ/ρ）与原子序数的关系

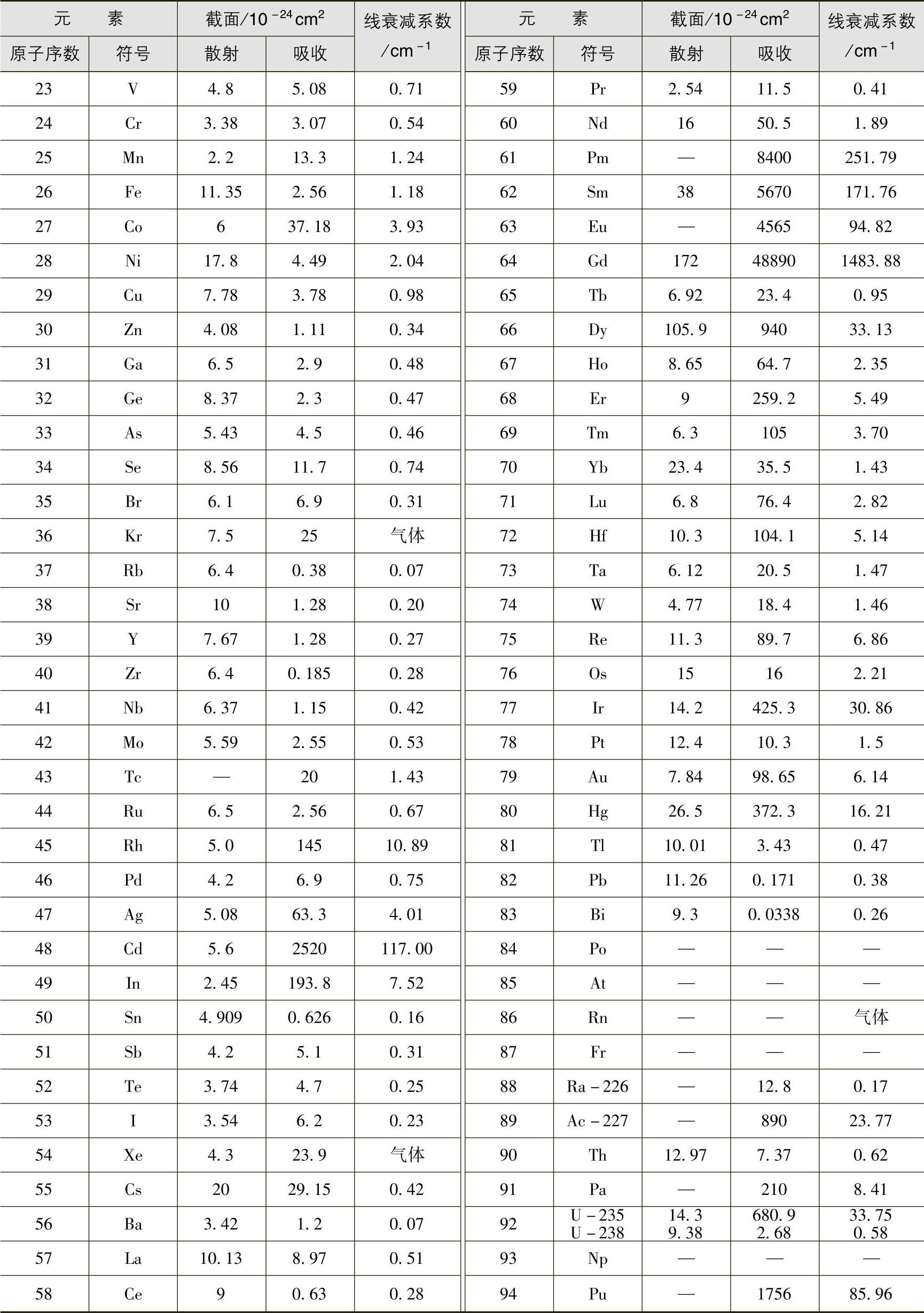
表2.3-1 用平均散射和吸收截面获得的自然元素的热中子线衰减系数

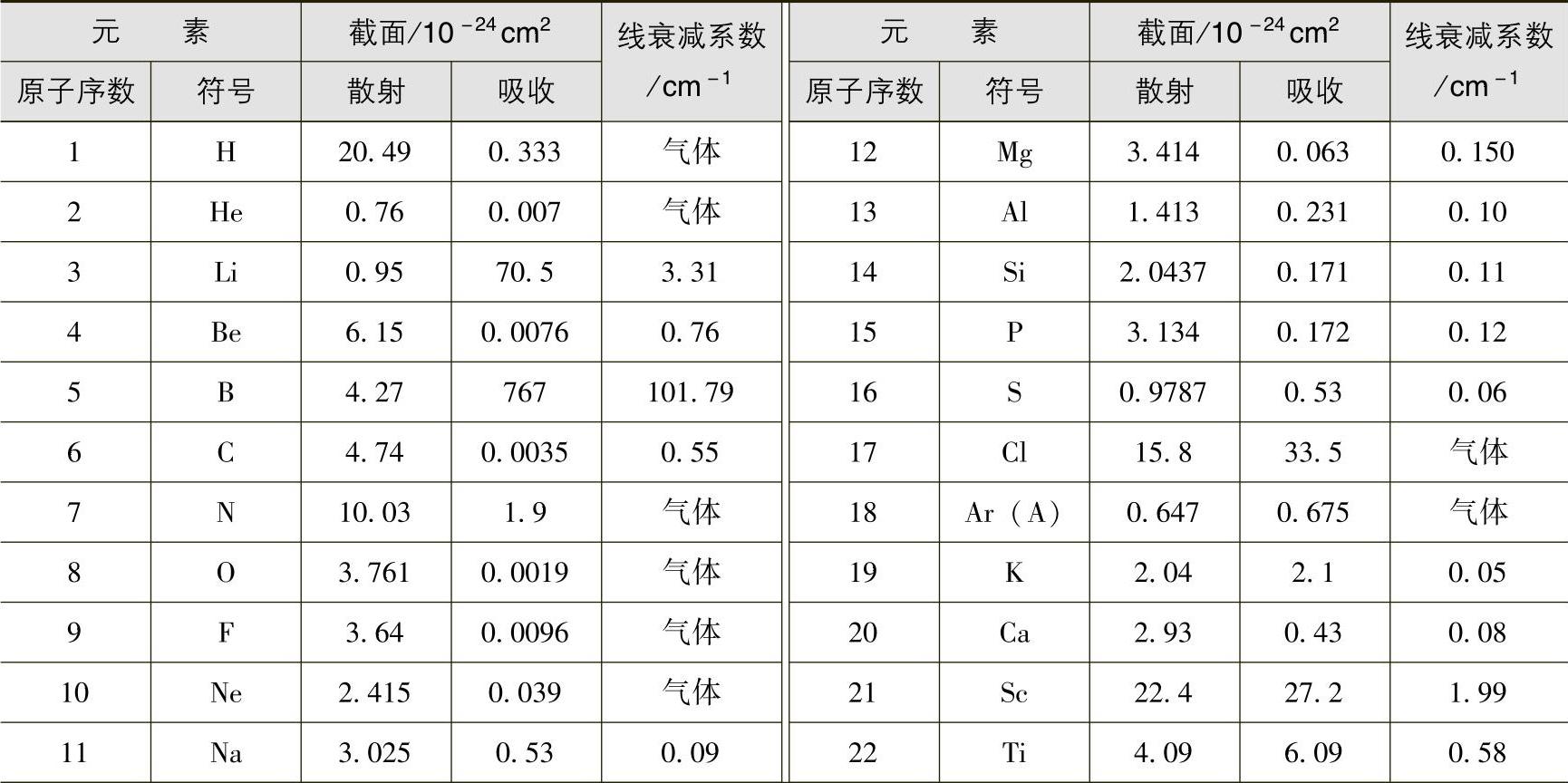
（续）