POD（a）函数的优化与二项式分布方法

对有相同人工缺陷的N个试样进行检测，结果只有两种可能，不是检出就是漏检，所以用二项式分布能得到最好的描述。

设在检测过程中检出有缺陷的试样数为S，其值可为0，1，2，…，N。S等于任一整数n（0≤n≤N）的概率可用下式描述，该式是二项式分布概率函数的标准形式

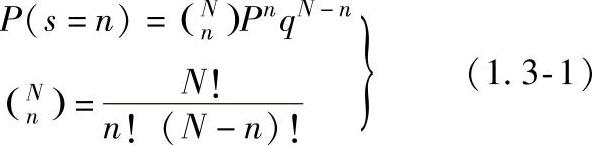
式中 P——真实的检出概率；

q——真实的漏检概率，q=1-P。将式（1.3-1）在S≥n的所有S值范围内求和，便可得到检出n个或更多个缺陷件的概率

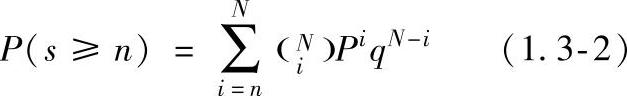
在观测总数不大的情况下，即30次或更少一些，应当使用此精确的二项式分布，对于给定的一组S、N及置信度G来说，可从下列表达式求得检出概率的下限Pl

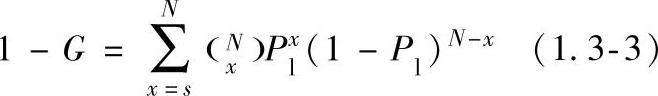
例如，如果N=20、S=14、G为0.95，则P_l便近似等于0.49。(www.xing528.com)

对于二项式分布法，选定了缺陷类型及尺寸，就必须确定所研究的那一尺寸的范围和该范围被分成的区间数以及所需试样数。对于某一尺寸区间，在某一特定置信度条件下，估算概率下限P_l所需的试样量可由方程式（1.3-3）算出，即根据所规定的置信度G以及概率下限P_l就能算出一组必须是整数的N和S的值。例如G和P_l分别为0.95和0.90，将之代入式（1.3-3）可得

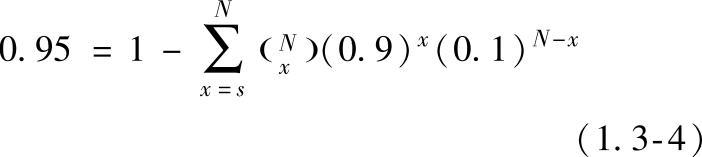
同样，G和P_l分别为0.50和0.90时，可得

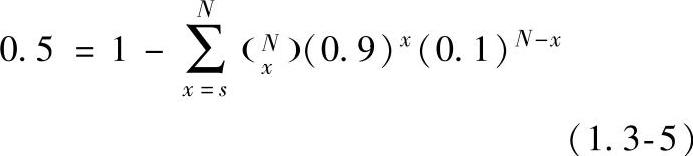
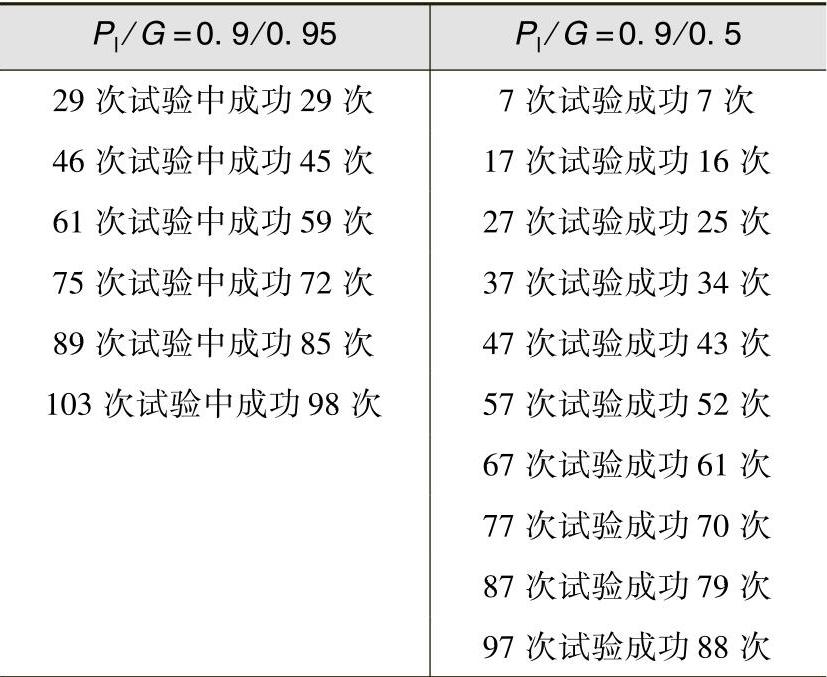
对P_l与G搭配为90/95及90/50时式（1.3-4）、（1.3-5）的各种解如表1.3-1所示。这样，在P_l/G=0.9/0.95的情况，缺陷的每一尺寸区间中必须有29件有缺陷的试样，如果将缺陷尺寸范围分成四个区间，则至少需要4×29=116个有缺陷的试样。除去有缺陷试样外，还必须有至少与有缺陷试样数量相等的无缺陷试样，两者相混，以便得出基本的不确定性。这种大量无缺陷试样的混入尚可提供一个试验环境，使试验人员仔细检查，因为很多试样是没有缺陷的。

表1.3-1 P_l/G为90/95及90/50时，N与S的搭配