改进分析型EAM模型（MAEAM）的优化探究

张邦维等人综合考虑以上各种EAM模型的优缺点后，一方面按照Pasianot的作法，在原EAM理论的基本表达式，即系统总能量表达式中经验地加入一修正项，用以描述两条基本假设所引起的能量偏离，并且具体给出了该修正项的分析表达式。另一方面，他们发展了一个能较好描述各种结构金属的原子间势函数的分析表达式，对于嵌入函数、原子电子密度和合金势，则仍然沿用Johnson的原有分析表达式。这样，他们所提出的分析型EAM理论对fcc，bcc和hcp各种结构的金属皆能进行描述，且能处理负Cauchy压的元素，成为一个普适分析型EAM模型。

在张邦维等人的普适分析型EAM理论中，对式（9-36）进行了修正，具体形式为

修正项M（P）的分析表达式为

两体势的分析表达式为

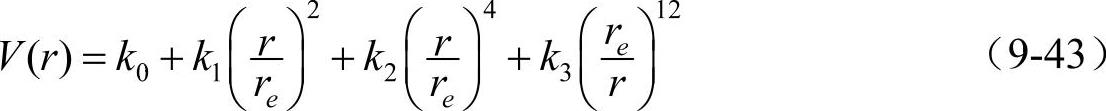
其中，下标e均表示平衡状态时的值。至于嵌入函数F（ρ）、原子电子密度φ（r）和合金势V^ab（r）则仍沿用Johnson所提出的分析形式表达式（9-37）～（9-40）。所有模型参数同样通过拟合纯金属的结合能、原子体积、体积模型、剪切模量和单空位形成能来确定。

此模型可很好地描述包括Cr在内的bcc金属，包括Cs在内的碱金属较好地描述hcp金属和fcc金属，由所确定的模型参数计算的弹性常数和空位形成能与实验测定结果符合较好。对bcc金属计算的单空位、双空位的形成能和迁移能与实验结果也很好相符。计算的各类金属间的二元合金稀溶解热和全成分范围的形成热也和实验结果基本相符。

胡望宇等在张邦维分析型EAM模型的基础上作了如下两点改进。

1）重新构造了金属的对势函数，并修改了原模型中的修正项的表达式，使该函数的函数值、一阶导数值和二阶导数值都比较小，以利于分子动力学的计算。

2）原模型中假定hcp金属均具有理想轴比，只用3个弹性常数拟合计算，对具体结构稳定性和空位移动能的计算与实验结果相差甚大。考虑到hcp金属的具体结构并运用全部5个弹性常数进行计算，重新构造了一个hcp分析型的EAM模型。

运用此模型计算了hcp金属的物性（包括声子谱、比热容、热膨胀等）、计算了晶体的点缺陷及扩散特性、层错和合金稀溶解热与形成热，计算结果与实验结果符合较好。

以上说明这种经验性的修正方法，尽管其物理意义有待进一步明确，具体函数形式有待进一步改善，却能直接明了地给出其分析模型，很有发展前途。

1.金属元素的MAEAM模型

本书所采用的改进分析型EAM模型（MAEAM），嵌入一个原子引起的能量变化仍采用式（9-39）的形式。考虑到计算上的方便，以嵌入原子为坐标原点，将能量表达式简化为

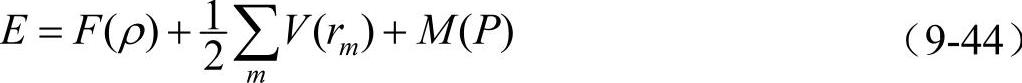
式中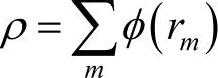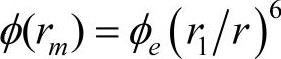，，，m代表第m近邻原子。其中的嵌入函数、原子电子密度及电子分布函数仍沿用Johnson的形式。

F₀的确定依据平衡条件下的能量关系得到

F₀=E_c-E_1f （9-45）

修正项M（P）的分析表达式为

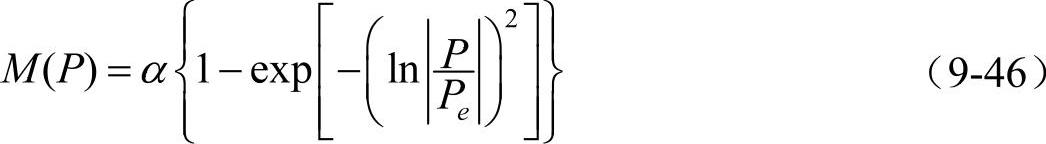
对于bcc，fcc金属的参量P表示为

对于hcp金属的参量P表示为

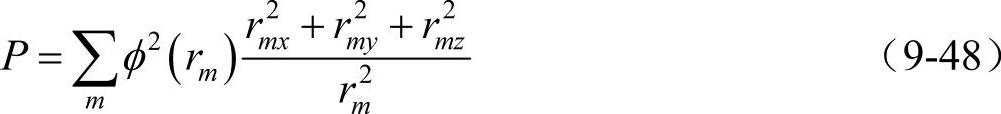
式中，rmx、rmy和rmz分别表示与原点原子相互作用的原子处于rm位置的各坐标分量。

对于势函数，在Johnson的模型中，是用一个三次多项式表示的，并在势函数两端分别进行挺坚和截尾处理，通过引入一个新的势函数多项式，可以不必进行挺坚处理。针对不同的晶体结构采用了不同的势函数形式。

（1）bcc金属的对势函数

Johnson和Oh最早提出bcc金属的分析型EAM模型，他们详细地阐述了构建分析型EAM模型的基本思路。张邦维等运用此模型对过渡族bcc金属的稀溶解热和形成热进行了计算，发现大多数合金系统的计算值与实验结果或Miedema的计算值是基本相符的，但Ta-W、W-M合金系的计算结果与实验结果相反，此模型还存在一个严重缺陷，就是不能处理负Cauchy压的元素与合金，为此张邦维对势函数进行了改进并加入一能量修正项，解决了此问题，并在后来的一篇论文中对这一改进分析型EAM模型（MAEAM）作了简单综述。

对于bcc金属，可采用如下对势函数式

在现在的模型中，原子间相互作用计算时只计及最近邻与次近邻的原子，V（r）函数在第二近邻与第三近邻之间截尾。截尾距离r_ce=r₂+k_ce（r₃-r₂），其中k_ce是一调节参数，通过拟合bcc金属的物理性质来确定。在该截尾处，势函数值和势函数的一阶导数值均为零，即：V（r_ce）=0，V′（r_ce）=0。

因此，可得到bcc金属的完整势函数为

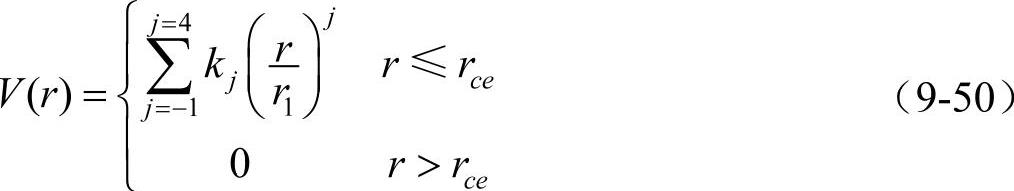
在计算结合能与原子体积关系时，为避免结合能不连续的问题，电子密度分布函数与势函数分别采用了不同的截尾处理。电子密度分布函数计算到第三近邻的原子，在第三近邻与第四近邻的四分之三处截尾。截尾距离r_cf=r₃+k_cf（r₄-r₃），其中k_cf取为0.75。在该截尾处，函数值和函数的一阶导数值均为零，即：φ（r_cf）=0，φ′（r_cf）=0。

势函数中的模型参数可以通过空位形成能、晶格平衡条件和弹性常数等物理性质来确定。

元素的未弛豫的空位形成能可近似用对势表示如下

在晶格没有应力时，晶体的平衡条件可以表示如下

bcc金属元素的弹性常数C_ijkl，可用下式计算

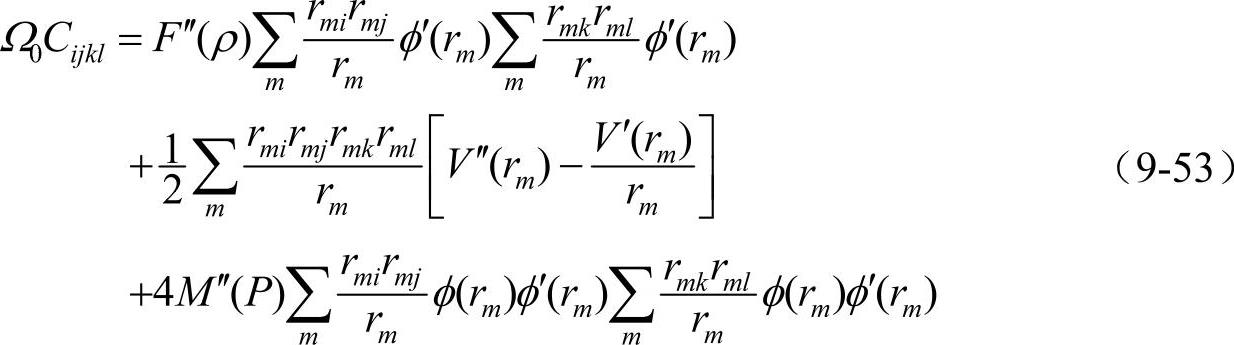
有三个独立的弹性常数，也就有三个方程。联立三个弹性常数方程和一个平衡条件方程，两个截尾条件方程和一个空位形成能方程就可以确定α和k_j（j=-1，0，1，2，3，4）7个模型参数。

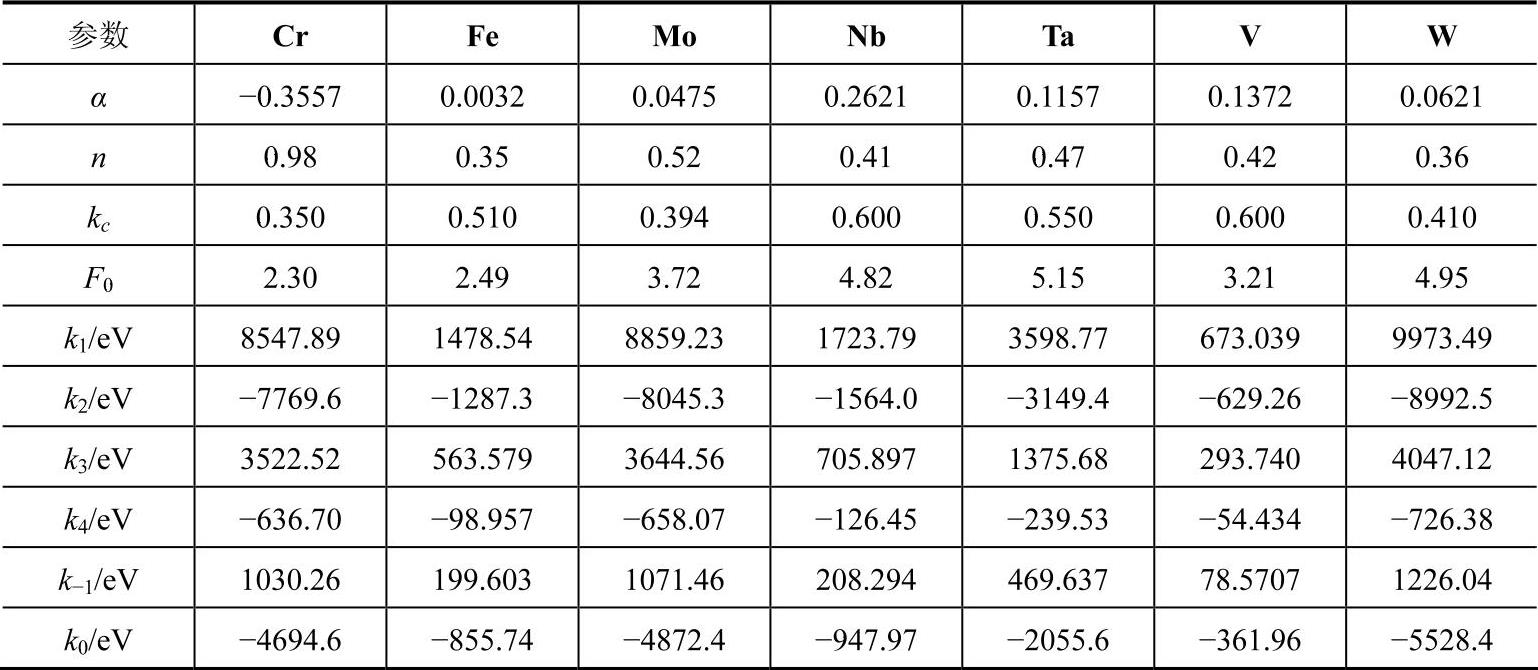
根据收集的有关资料，整理了过渡组bcc金属元素的输入参数（列于表9-1中），舒小林根据表9-1中的bcc金属元素输入参数，计算得到了该模型参数（见表9-2）。

表9-1 bcc金属元素的输入参数

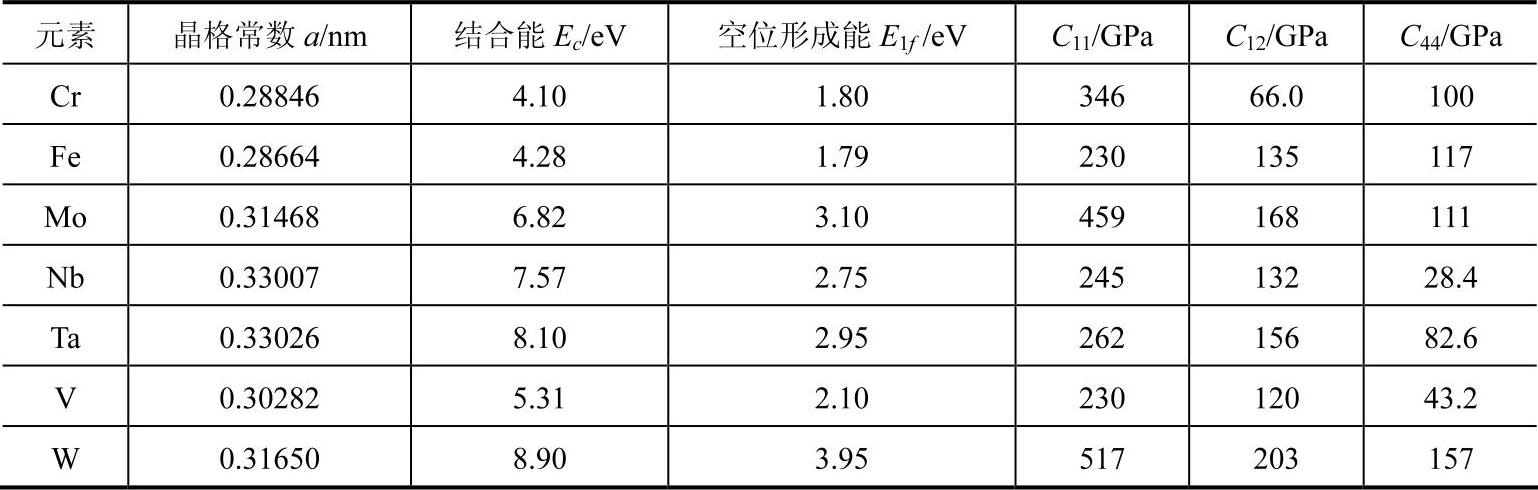
表9-2 bcc金属元素的模型参数

（2）fcc金属元素的对势函数

fcc金属分析型EAM模型最初由Johnson在1988年提出，当时只考虑最近邻原子的相互作用，给出了建立分析型EAM模型的基本思路。随后，Johnson建立了具体的计算方法并考虑了更远近邻原子的相互作用。为了体现模型的应用价值，他们用所建模型计算了几种fcc金属形成二元合金的形成热，计算结果和实验结果及第一原理的计算值大致相符。由于Johnson模型不能处理负Cauchy压元素，张邦维等对Johnson模型进行改进，试图发展一种普适分析型的EAM模型，并据此重新计算了fcc金属二元合金的形成热，计算时考虑了最近邻和次近邻原子的相互作用，采用和bcc金属完全相同的势函数，所得结果比Johnson的略有改善。运用此模型处理fcc金属的扩散问题时，发现计算的空位迁移能大大小于实验结果，个别元素甚至出现负的空位迁移能，说明模型在处理元素特性问题时就不能自洽。胡望宇等在其模型中对势函数和模型方程进行了调整，并考虑到第五近邻原子的相互作用，解决了元素特性自洽性问题。

fcc金属采用了如下形式的势函数

在通常使用的模型中，fcc金属原子间相互作用计算时计算到第五近邻的原子，V（r）函数在第五近邻与第六近邻之间截尾。截尾距离r_ce=r₅+k_ce（r₆-r₅），其中k_ce是一调节参数，通过拟合fcc金属的物理性质来确定。在该截尾处，势函数值和势函数的一阶导数值均为零，即：V（r_ce）=0，V′（r_ce）=0。

在计算结合能与原子体积关系时，为避免结合能不连续的问题，fcc金属的电子密度分布函数仍采用了不同于势函数的截尾处理方式。电子密度分布函数φ（r）计算到第六近邻的原子，在第六近邻与第七近邻的四分之三处截尾。截尾距离r_cf=r₆+k_cf（r₇-r₆），其中k_cf取为0.75。在该截尾处，函数值和函数的一阶导数值均为零，即：φ（r_cf）=0，φ′（r_cf）=0。

fcc金属的势函数中模型参数同样可以通过空位形成能、晶格平衡条件和弹性常数等物理性质来确定。

对于电子密度φ（r）及参数F₀的计算方法和bcc金属的完全相同，但fcc金属的原子体积Ω₀=a³4（a为晶格常数）。

于是可得到fcc金属的完整势函数

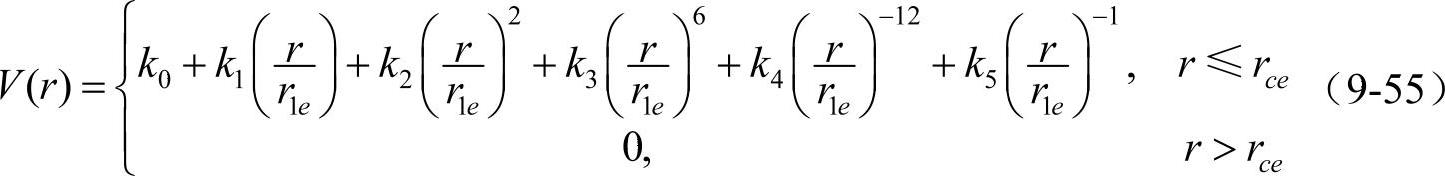
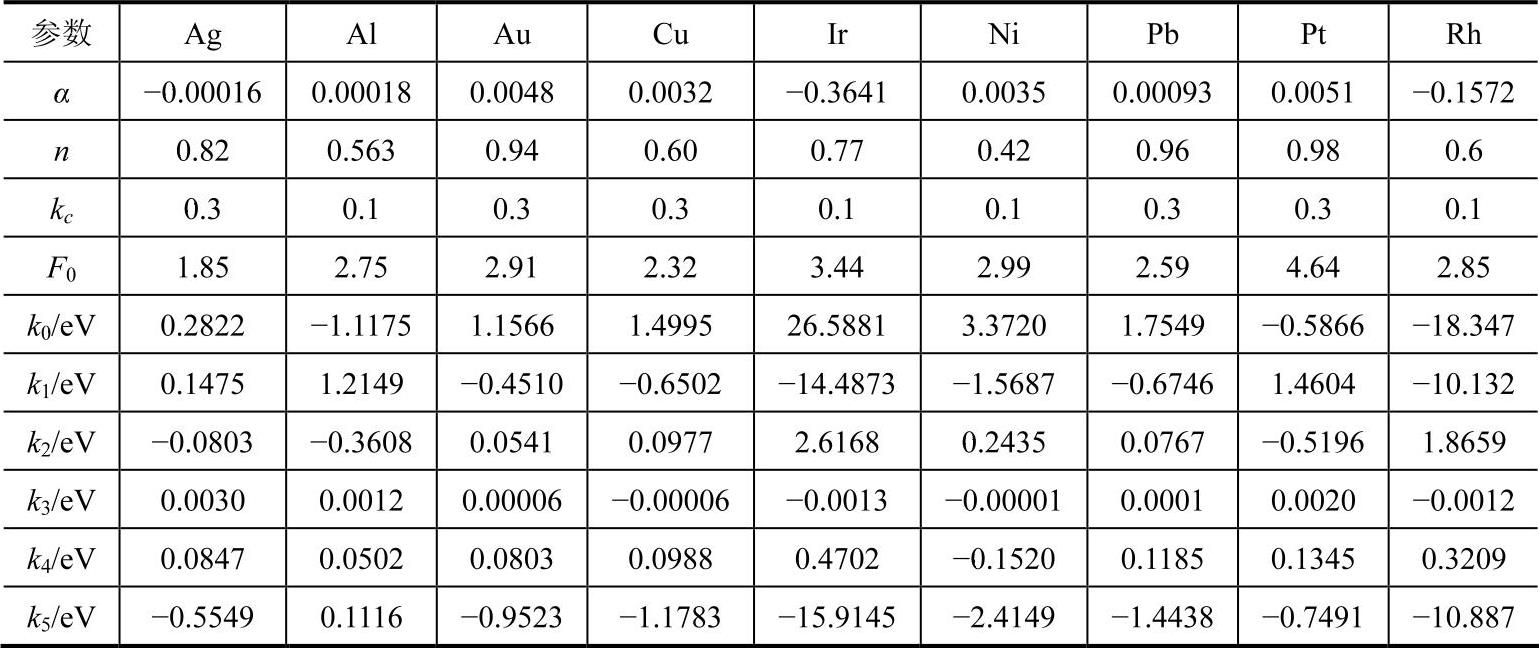
表9-3为根据收集的有关资料整理的过渡元素Ag、Al、Au、Cu、Ir、Ni、Pb、Pt和Rh 9个fcc金属的输入参数，表9-4为舒小林根据表9-3中的数据对fcc金属元素计算得到的模型参数。

表9-3 fcc金属的输入参数

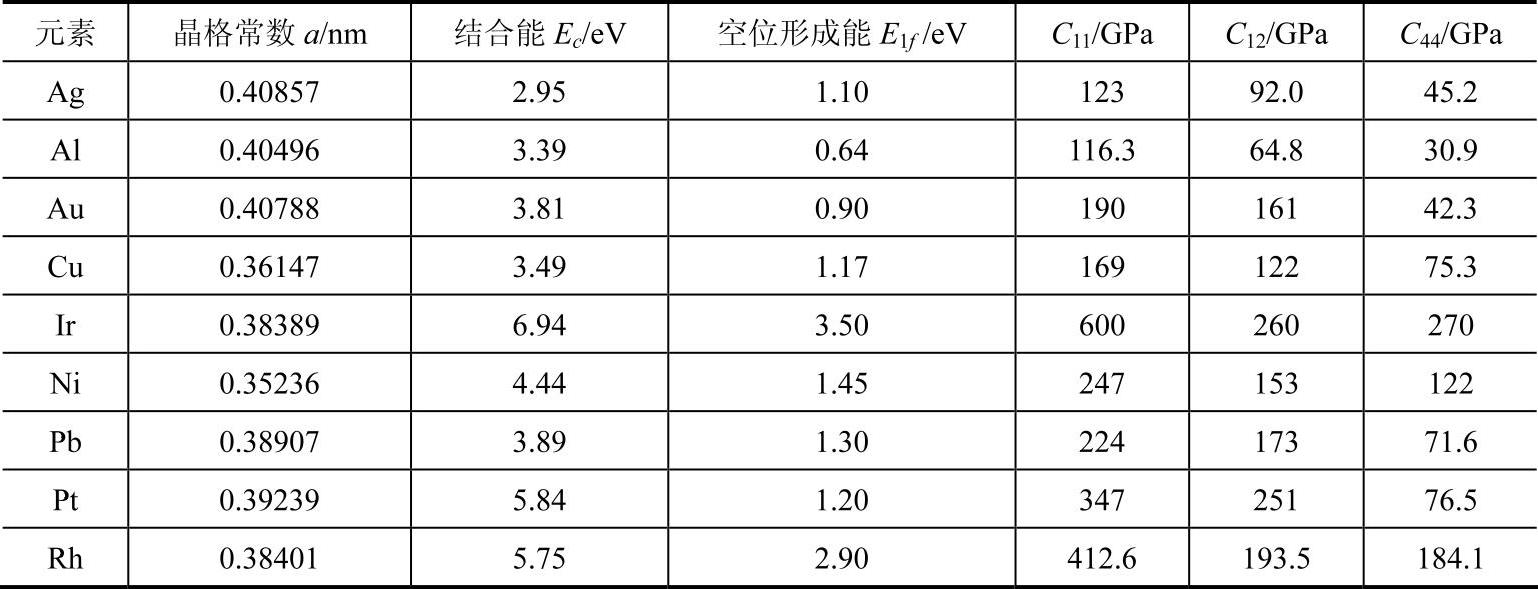
表9-4 fcc金属的模型参数(www.xing528.com)

（3）hcp金属的对势函数

对立方晶体结构的bcc和fcc元素，无论是FS还是EAM多体势都取得了较大进展，对这些金属组成的合金系统的原子模拟也相当成功，如对镍铝合金系的物理及力学性能的预测。相对而言，对hcp金属多体势的研究进展就甚为缓慢。正如Bacon教授对hcp金属计算机模拟的综述文章所言，hcp金属晶体缺陷的模拟计算大多还是沿用两体势，且只能近似描述c/a比接近理想轴比的元素，尽管已开始发展hcp元素的多体势，但能满足具体模拟计算多项判据要求的多体势还远未构成，因此，构建hcp元素完备的多体势就成了发展原子尺度材料设计理论的当务之急。

20世纪80年代末期，Johnson首先构筑了hcp元素（Mg、Ti、Zr）的分析型EAM多体势，只采用一个平衡条件，通过拟合结合能、空位形成能、平均体模量和剪切模量来确定模型参数，由此模型计算的5个弹性常数与实验值符合较好，但c/a比却接近理想轴比，因此偏离理想轴比较大的元素就不能采用此模型计算。为了发展更普遍适应的hcp元素的多体势，Igarashi和Vitek等人构筑了Be、Hf、Ti、Ru、Zr、Co、Mg、Zn 8个hcp元素的FS多体势，这是截至目前为止处理hcp元素最成功的多体势，计算了层错能、声子谱和自间隙原子特性，但由于没有拟合原子平衡距离之间的任何信息，使得所构多体势非常硬，计算的自间隙原子形成能特别大，因此在原子模拟计算中没有被采用，而且不能应用于合金系的计算。Pasianot认为这些多体势的问题在于没有考虑晶格内禀自由度对弹性常数的贡献，因而就构筑了Hf、Ti、Mg、Co的EAM多体势，但他仅计算了这些元素的层错能，对空位、间隙原子等未作计算，模型的合理性不得而知，也就没引起人们的注意。关于hcp金属EAM多体势处理元素最多的是Johnson和Baskes，在1994年发表的论文构筑了18个hcp元素的多体势，由于采用Baskes定向键修正思想，使得计算过程非常复杂。他们仅计算了空位、层错和表面特性，计算的双空位结合能与实验结果完全相反，且未对自间隙原子特性作任何报道，他们还允诺发表应用于hcp金属合金系统上的结果，但至今未见发表出来，说明模型存在较大问题。为了得到实用的hcp金属多体势，Ackland进行了简化处理，在拟合三个弹性常数和一个晶格常数基础上构筑了关于Ti和Zr的FS多体势，并应用于核辐照联级碰撞中晶体缺陷形成过程的模拟计算，较好地解释了相关实验现象，但模型过于简化，只能处理接近理想c/a比的元素，不能推广到一般的hcp元素。

从以上事实可以看到，关于hcp元素多体势的研究引起了国际学术界的普遍关注，是材料设计领域的一个国际难题，同时hcp金属元素中包括了许多极有应用价值的元素，如Ti、Mg、Hf、Co、Be、Zn是重要的有色金属，Zr、U是核材料中不可缺少的元素，Nd、Pr、Tb、Y、Dy、Er、Ho、Gd等稀土元素在稀土合金中应用广泛，Os、Re是高密度合金的重要组元等。发展hcp元素的多体势并开展有关性能或过程的模拟计算，将会极大地促进有色金属合金和稀土合金的开发和应用。因此，发展系统而完备的hcp元素的多体势并进行原子模拟和性能预测不仅具有重要的科学意义，也具有难以估量的潜在应用价值。

hcp金属的结构与立方晶体相比有显著差异，对于立方晶体只有7个模型方程，即3个弹性常数方程、1个平衡方程、1个空位形成能方程和两个势函数截尾条件方程，可确定7个模型参数，其中势函数的6个参数和修正函数中的一个参数。在hcp金属中，有5个独立的弹性常数，即5个弹性常数方程，由于a轴与c轴的各向异性存在2个平衡方程，1个空位形成能方程，再加上2个势函数截尾条件方程，共有10个模型方程。为了描述电子密度高次项的各向异性效应，在修正函数中须引入1个各向异性修正因子，因而修正函数中包含2个模型参数，这与hcp金属存在2个Cauchy关系相对应，其余8个模型参数放在势函数中。对于hcp金属所考虑的近邻数也有较大差异，通过对比计算发现计算到原子第七近邻相互作用结果较为理想。

势函数的形式为

对电子密度高次项贡献因子P的计算与立方晶体不同，对于立方晶体，只有一个Cauchy关系，原子的排列呈现立方对称，因而修正函数只包含一个模型参数。对于hcp金属，存在两个Cauchy关系，且原子排列呈现各向异性，为了计入这种各向异性，在计算P时就引入一个各向异性因子，对于参考原子位于坐标原点（0，0，0）时的形式为

式中，rmx、rmy和rmz分别表示与原点原子相互作用的原子处于r_m位置的各坐标分量。

在本书使用的模型中，hcp金属原子间相互作用计算时计算到第七近邻的原子，V（r）函数在第七近邻与第八近邻之间截尾。截尾距离r_ce=r₇+k_ce（r₈-r₇），其中k_ce是一调节参数，通过拟合hcp金属的物理性质来确定。在该截尾处，势函数值和势函数的一阶导数值均为零，即：V（r_ce）=0，V′（r_ce）=0。

在计算结合能与原子体积关系时，为避免结合能不连续的问题，hcp金属的电子密度分布函数仍采用了不同于势函数的截尾处理方式。电子密度分布函数φ（r）计算到第八近邻的原子，在第八近邻与第九近邻的四分之三处截尾。截尾距离r_cf=r₈+k_cf（r₉-r₈），其中k_cf取为0.75。在该截尾处，函数值和函数的一阶导数值均为零，即：φ（r_cf）=0，φ′（r_cf）=0。

hcp金属的势函数中模型参数同样可以通过空位形成能、晶格平衡条件和弹性常数等物理性质来确定。

于是可得到hcp金属的完整势函数

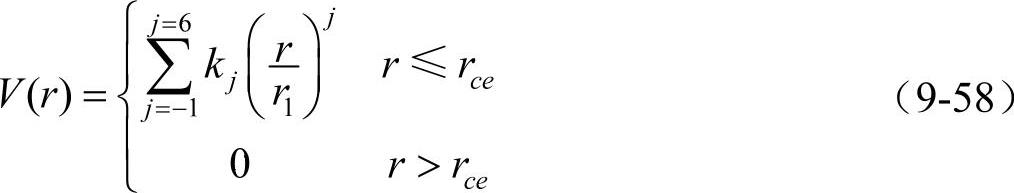
hcp元素的未弛豫的空位形成能的对势形式与bcc元素相同。

由于P的变化将会引起弹性常数C_ijkl的变化，因此，hcp元素C_ijkl与bcc元素的有所不同，其计算公式如下

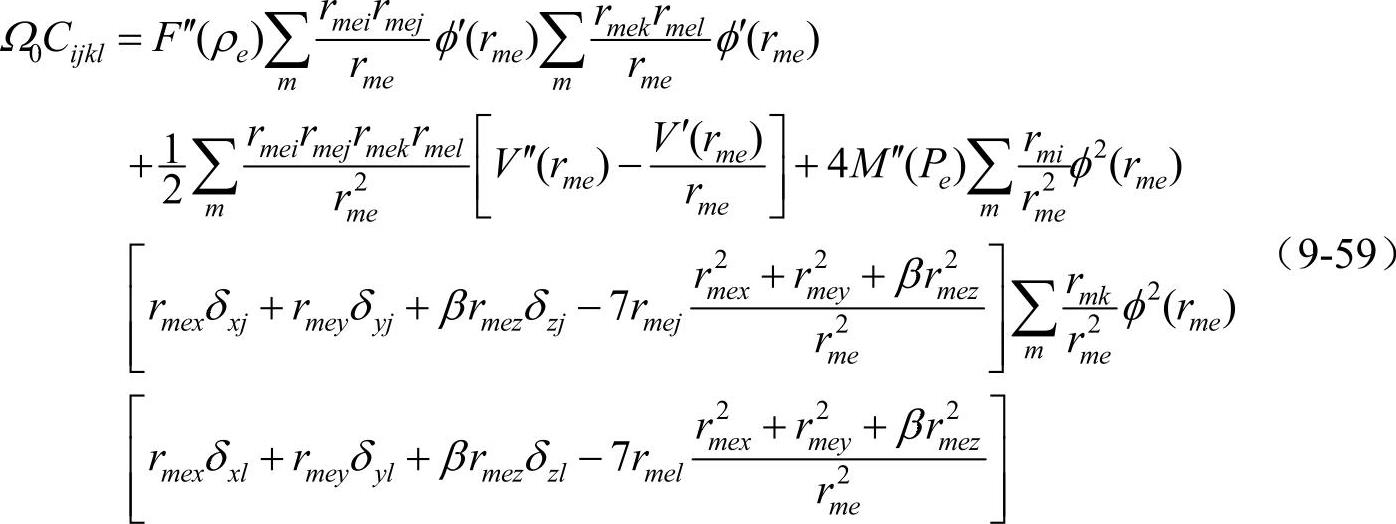
据此就可计算hcp金属的5个独立弹性常数。这样就确定了修正函数所包含的2个模型参数（α和β）和势函数中的8个模型参数（j=-1，0，1，2，3，4，5，6）。

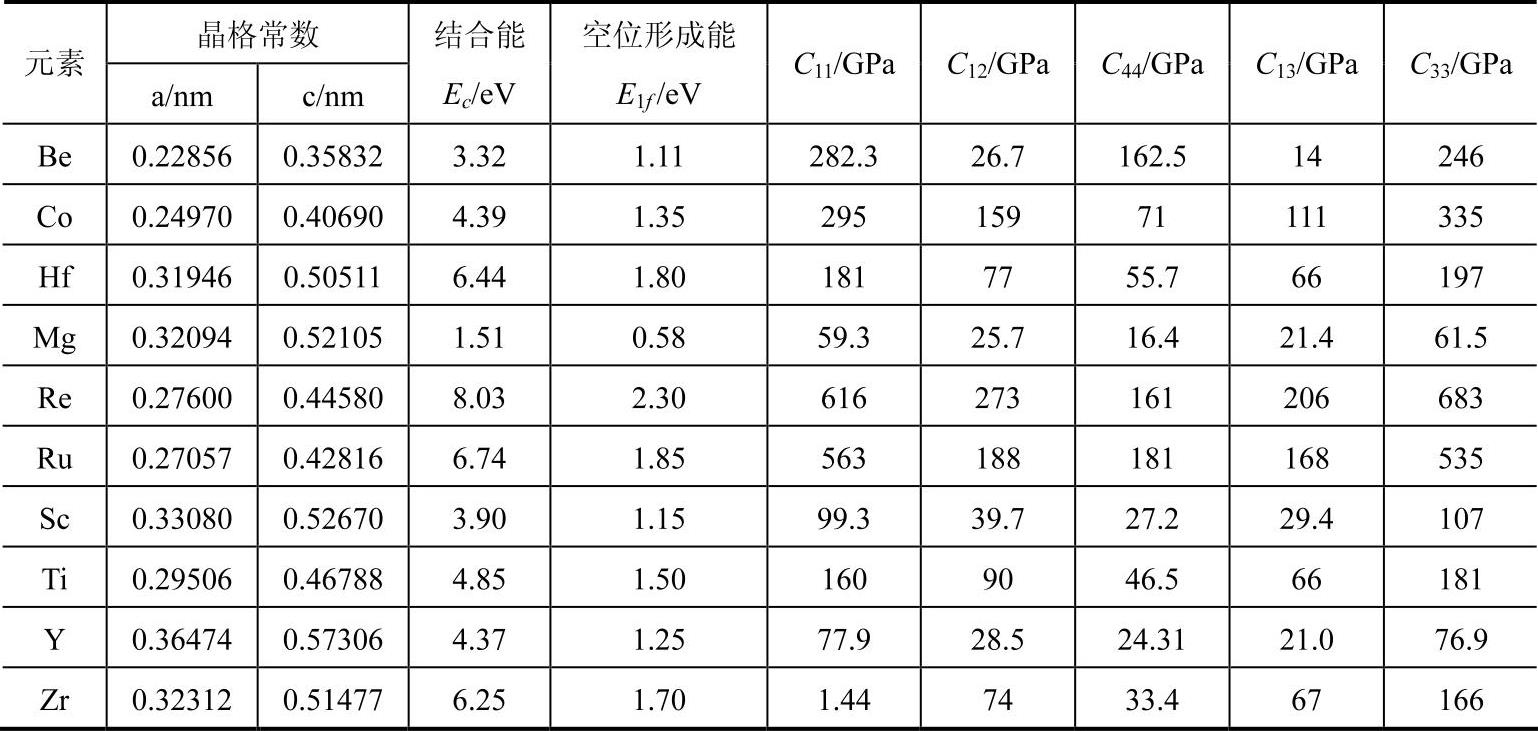
电子密度、嵌入函数和修正函数完全可按照前面的计算方法来确定。hcp结构金属的晶格常数、结合能、空位形成能和弹性常数等输入参数如表9-5所示。

表9-5 hcp金属的输入参数

（4）模型参数φ_e的确定

MAEAM模型中使用的电子密度函数是沿用Johnson的形式。电子密度函数表达式中的前因子φ_e的值原则上可以通过拟合Clementi和Foetti基于Hartree-Fock理论计算的结果来确定。

在实际应用中，φe的值有两种确定方法：

1）Foiles的方法。利用合金系统已有的热力学性质来确定合金中各组元素的相对值。

2）Johnson的方法。采用经验关系式来表示，如定义φ_e为能量密度，取φ_e=E_cΩ。

Zhan等在其应用中取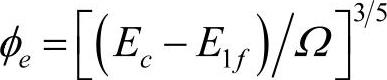。胡望宇考虑到能量是电子密度的平方取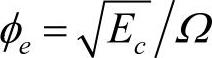。在将该模型应用于金属元素的计算时，电子密度是以比值形式出现在嵌入能表达式中的，电子密度函数表达式中的前因子几乎被约化掉了，其值的大小不会影响计算结果。但应用于合金的计算时，该参数不能被约化，因而在改进分析型EAM模型应用于合金系统时，必须先确定φ_e的值。

下面仍采用类似于Johnson的方法，通过反复计算和比较，建立电子密度函数表达式中的前因子f_e与元素的物理量之间的关系。

考虑到φ_e表示金属元素处于平衡状态时的电子密度，这个量应与元素的电子因素密切相关。它与合金中元素吸引电子的能力有关，即与电负性等物理量相关，电负性大吸引电子的能力强，电子密度大。此外，它也与合金中元素所占体积有关，对于同一电荷数量来说，元素体积大，电子密度小。金属间化合物的有序结构对电子密度的影响我们认为可以通过化学标度来描述。

基于上述考虑，φ_e可采用了如下的经验关系

其中：

1）c为系数，对AB类金属间化合物，密堆结构的Ni、Co、Al的c取为1；bcc金属Fe，考虑到其非密堆结构的影响，c取为（0.74/0.68）3，对Ti元素c取为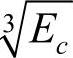。对A₃B类金属间化合物，由于成分的变化引起电子分布变化，A元素的φ_e计算公式中再乘以一个因子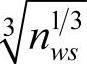。表9-6为一些AB型合金和A₃B型合金所使用的φe值。

2）φ*为Miedema模型中的参数—功函数，该参量类似于元素的电负性参量，是一个描述元素的电子因素的参量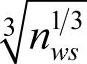；是Miedema模型中定义的Wigner-Seitz原胞边界的电子密度，也是一个描述元素的电子因素的参量。

表9-6 模型参数φ_e值

3）χ为Pettifor提出的元素“化学标度”。国际材料科学组织（MSIT）在1990年决定采用以Pettifor提出的这个参量来确定化学式中元素顺序。这个参量就是所谓的门捷列夫数（M）及相关的“化学标度χ”。

关于φ_e的进一步研究，将依据量子力学对原子电子密度的具体计算并考虑元素间合金化效应来计算，这个问题有待日后的深入研究来解决。

2.金属间化合物的物理性质及点缺陷的计算方法

（1）晶格常数和弹性常数的计算方法

金属间化合物晶格常数的计算：给定金属间化合物的初始晶格常数值，构造出所要研究的晶体结构。使用分子动力学程序对该晶体结构进行弛豫，使其达到平衡状态，此时所得的晶格常数即为本书的计算结果，也是其他物理性质和点缺陷研究的基础。

金属间化合物弹性常数的计算：按Johnson的方法对能量展开

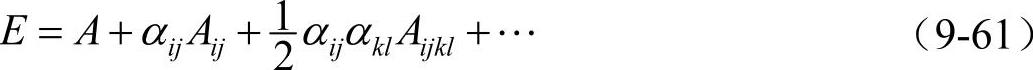
其中：

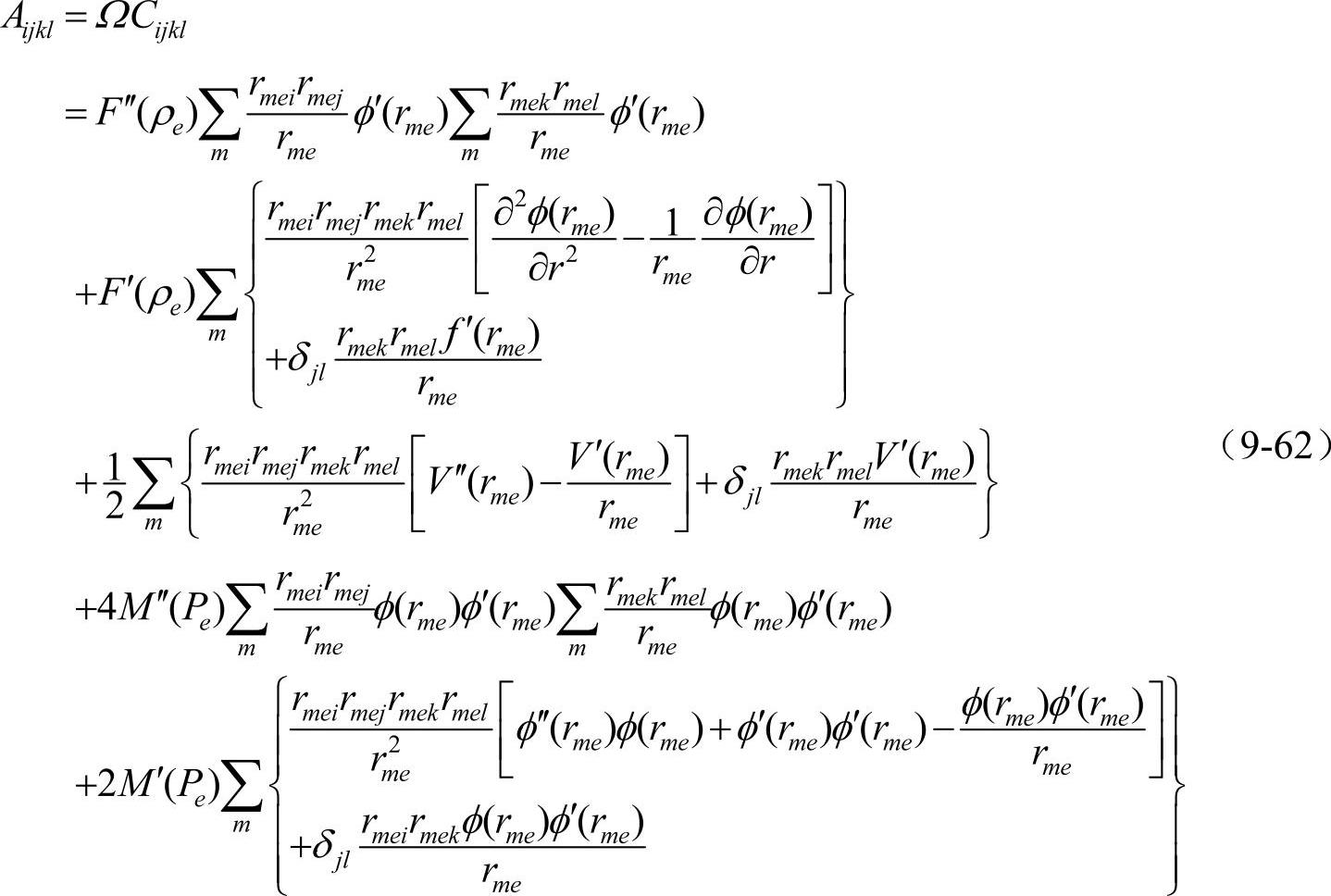
式中，Ω为原胞中原子平均体积。

由已计算出的晶格常数值即可计算出金属间化合物的弹性常数。

（2）金属间化合物的点缺陷及扩散性质的计算

B2结构金属间化合物AB的晶体结构是体心立方为基的有序结构，由一种元素（如A）占据bcc晶胞的体心位置构成的简单立方子晶格（称α子晶格），另一元素（如B）占据晶胞的顶角位置构成的简单立方子晶格（称β子晶格），两个子晶格互相穿插构成有序结构。L12结构金属间化合物A₃B的晶体结构是以面心立方为基的有序结构，A原子占据面心立方中面心的位置，B占据顶角位置。L10结构金属间化合物AB的晶体结构也是以面心立方为基的有序结构，A、B原子分别分层占据面心立方中（001）面，沿[001]方向按ABAB…重复排列而成。

完整晶体结构只在绝对零度理想化学配比成分下出现。在一定温度下，晶体中出现的点缺陷称为热缺陷：为容纳合金与理想化学配比成分的偏离出现的点缺陷称为结构缺陷。在这种有序结构中可能出现四种结构点缺陷：A原子占据β子晶格形成A反位置缺陷，B原子占据α子晶格形成B反位置缺陷，α子晶格中形成A空位和β子晶格形成B空位。

模拟过程中得到的各种点缺陷能量由下述公式给出。

对过渡元素（TM）和Al原子的单空位

对过渡元素（TM）和Al原子的双空位

对过渡元素（TM）和Al原子的反位置缺陷

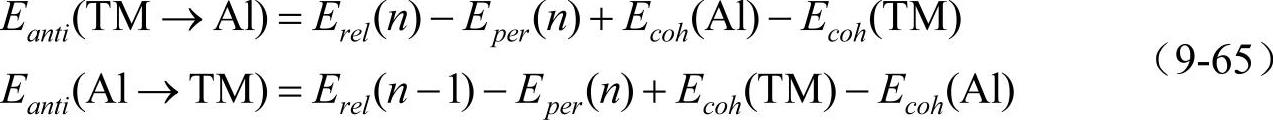
式中，E_v表示单空位的形成能，E_2v表示双空位的形成能，E_anti表示反位置缺陷的形成能，E_per（n）表示n个原子组成的完整晶格的总能量，E_rel（n-1）表示引入一个点缺陷后余下的（n-1）个原子组成晶格的总能量，E_coh（TM）和E_coh（Al）表示单个TM原子和Al原子的结合能。

金属间化合物中原子扩散的研究：根据扩散空位机制，原子通过空位而迁移，邻近空位的原子向空位迁移时必须克服周围原子相互作用所构势垒的束缚，通过计算发现势垒的最高点位于原子迁移路途的中点，迁移原子处于此位置时的能量与处于平衡位置的能量差即为空位迁移能E_lm=E_1f-E₀。原子的扩散激活能Q_1v，Q1v=E1f+E1m。

分别计算了原子扩散过程弛豫和未弛豫的能量。未弛豫的原子扩散研究是分别计算扩散路径各点的能量及扩散过程的迁移能和激活能，没有考虑分子动力学弛豫。弛豫的原子扩散研究是把原子放在扩散路径的鞍点上，作分子动力学弛豫，原子将在鞍点作弛豫并逐渐向空位移动，最后到达格点位置，在弛豫过程中对各点的能量取样即可计算出原子扩散的迁移能和激活能。