弹性性质的第一性原理计算：探究TiB的特性

TiB因其具有高的弹性模量而在钛基复合材料中作为增强体，备受重视。一般材料的弹性模量可以通过实验方法测得，但对于难以测试的块体材料（如TiB）或材料中析出相的弹性模量存在一定困难。近几年来，由于第一性原理对材料弹性性质的理论计算结果与实验值有很好的一致性，因此已成为研究材料弹性性质的重要手段。

TiB属于正交晶系，其空间群为P6/mmm，单胞中含有3个原子，具有9个独立的弹性常数（C₁₁，C₂₂，C₃₃，C₁₂，C₁₃，C₂₃，C₄₄，C₅₅和C₆₆）。下面是利用基于密度函数理论和赝势平面波方法计算得到的TiB弹性性质。

采用计算得到的弹性常数可以计算出TiB的体模量B、弹性模量E、切变模量G和泊松比ν等弹性性质参数。在多晶材料弹性模量的理论估算方面，Hill通过极值原理证明，Voigt和Reuss模型的计算结果是弹性常数的上下限。Hill模型则将Voigt和Reuss模型的计算结果取一个简单的算术平均即VRH平均，其结果和实际测定值更为一致。Hill模型即VRH平均法计算多晶体材料体模量B和切变模量G的计算式为

采用Voigt和Reuss模型计算正交晶系晶体的K和G的计算为

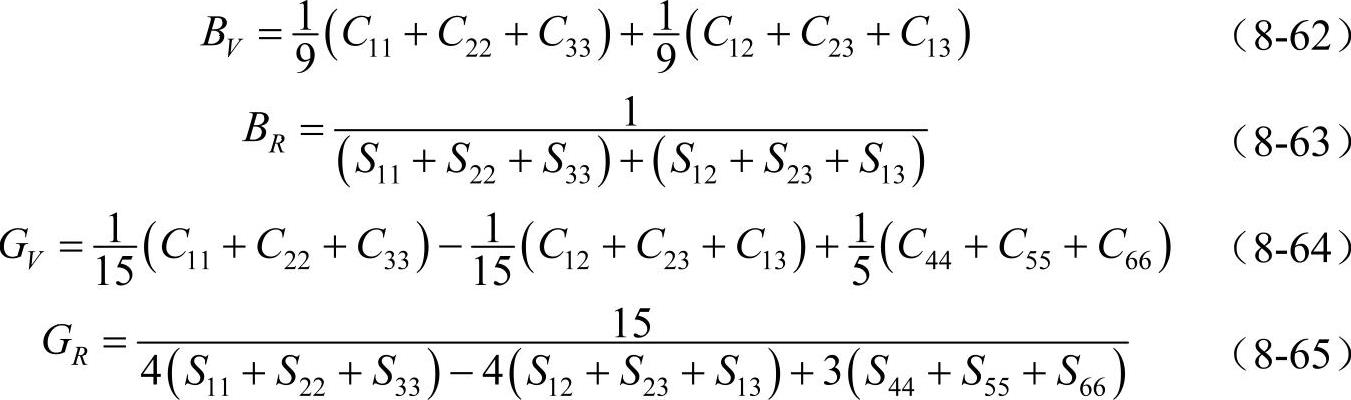
式中，S_ij为Cij的逆矩阵。弹性模量E和泊松比ν的计算式为

(www.xing528.com)

采用上述公式用表8-4TiB材料的弹性常数可计算出TiB材料的弹性模量E、切变模量G、体模量B和泊松比v（见表8-5）。

表8-4 TiB晶体的弹性常数（GPa）

Pugh曾提出过一个预测材料的延/脆性的经验判据，即通过切变模量G与体模量B的比值来判断金属材料的延性或脆性。如果这一比值G/B<0.5，材料呈延性；反之，材料则呈脆性。这一判据已被广泛应用于分析金属间化合物和类金属间化合物的延性或脆性。从表8-5可以看出，TiB G/B值远大于0.5，说明TiB是具有很大脆性的化合物。另外，泊松比ν的大小也可用来衡量金属和金属间化合物的脆性。对延性材料而言，泊松比一般为1/3；而脆性材料的泊松比一般小于1/3。由表8-5可知，材料TiB的泊松比远小于1/3，所以再次说明TiB是具有很大脆性的化合物材料。

表8-5 TiB材料的体模量B（GPa）、切变模量G（GPa）、弹性模量E（GPa）和泊松比v