晶体物理性质的计算方法简介

利用自洽场方法求解科恩-沈[吕九]方程，得到所设结构的晶体总能量（单点能）。在计算晶体的物理性质之前必须对所设晶体结构模型进行几何优化，根据关于能量、力、应力、位移的判据来判断晶体结构是否为稳定结构（总能量最小）。如果晶体结构不是稳定结构，重新设置晶格参数进行计算，直至得到稳定的晶体结构。对结构优化后的晶体进行物理性质计算，最后输出计算结果。

1.晶体的总能量

晶体总能量（不包括核的动能部分）可分成两部分：一部分是原子核与内层电子组成的离子实的能量，这部分能量基本上与晶体结构无关，是一个常数，赝势方法中常把总能量中这部分不变的能量设为零；另一部分是总能量与离子实能量之差，包括离子实与价电子的相互作用、离子实之间的相互作用以及价电子间的相互作用。晶体总能量与核动能（通常是零点振动能）之和与全部组分原子的孤立原子能之和的差，称为晶体的结合能。

在密度泛函理论中，晶体总能量E_T是晶格电子的能量与离子实的排斥能之和

各项的物理意义与方程（8-11）和方程（8-12）中的相同。其中电子与外场v（r）的相互作用能为

电子间库仑相互作用能为

在局域密度近似条件下，电子的交换关联能为

离子实之间的库仑相互作用解为

这里Z_s表示原子s的价电子数，R表示晶格平移矢量，τ_s表示原胞内原子s的相对位矢。动能泛函可通过科恩-沈[吕九]方程用单电子能量表示为

这里E_i是科恩-沈[吕九]方程的本征值。将式（8-50）～式（8-52）、式（8-54）和式（8-19）代入式（8-49），得到晶体总能量(www.xing528.com)

晶体的单电子能E与晶体体积NΩ之间的关系可用Murnaghan状态方程

来描述。方程（8-56）中N是晶体中原胞的数目，Ω是晶格常数尝试值为a时的原胞体积，B₀是体弹性模量，B₀′是B₀对Ω的导数。对于不同的晶格常数尝试值a，即不同的晶体体积NΩ，可计算出相应的单点能E（NΩ），用最小二乘法拟合Murnaghan状态方程，便可得到相应于该结构的晶体常数a₀、体弹性模量B₀和该结构的能量极小值E（NΩ₀）。

对于组成元素确定的体系，可能存在不同的晶体结构。分别对不同的晶体结构进行总能量计算和Murnaghan方程拟合，得到相应的能量极小值E（NΩ₀），比较不同晶体结构的能量极小值，便可确定稳定的晶体结构。

由晶体总能量可以确定晶体的一些力学性质，如赫尔曼-费恩曼（Hellmann-Feynman）力和应力。作用于原子s上的力F_s可由晶体总能量E_T对原子s的原胞内位矢τ_s求负梯度得到，即F_s=-∇τ_sE_T，这个作用于原子上的晶体内力称为赫尔曼-费恩曼力。对于晶格应变张量ε=ε_αβ，平均应力张量为σ=σ_αβ，则。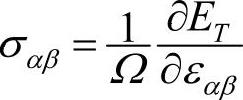

2.弹性常数

不同晶系的晶体具有不同数量的独立弹性常数。立方结构的晶体存在3个独立的弹性常数（C₁₁，C₁₂和C₄₄），六方晶系具有5个独立的弹性常数（C₁₁，C₁₂，C₁₃，C₃₃和C₄₄），而正交晶系则具有9个独立性常数（C₁₁，C₂₂，C₃₃，C₁₂，C₁₃，C₂₃，C₄₄，C₅₅和C₆₆）。材料的弹性常数描述了它对所加应力的响应，或者反过来说，弹性常数描述了为维持一个给定的形变所需的应力。

为了计算晶体的弹性常数，可先对晶胞进行不同的弹性变形，然后算出变形后的能量，并通过此能量与未变形晶胞的能量差，求出弹性应变能，进而利用弹性常数与应变能的关系计算得到弹性常数。弹性应变能计算式为

其中ΔE为变形前后晶胞的能量差值；V₀为原始晶胞的体积；C_ij为弹性常数；e_i和e_j为应变。