固体能带计算方法及其应用

固体能带理论是研究固体中电子运动的一个重要理论，是固体电子论的支柱。建立布洛赫（Bloch）定理之上的固体能带理论用量子力学方法来确定固体电子能级（能带），并用以阐明和解释固体的许多基本性质，如电导率、热导率、磁有序、光学介电函数、振动谱等。本节主要介绍能带理论的理论基础、基本概念、能带计算方法以及应用能带理论对固体物理性质的计算。

能带理论是一个近似理论。固体中有大量的原子核和电子，严格求解这种多粒子系统的薛定谔方程是不可能的，必须采用一些近似和简化。能带理论采用了如下三个近似：

1）玻恩-奥本海默Born-Oppenheimer近似（绝热近似），将原子核的运动与电子的运动分开。

2）单电子近似，把每个电子的运动看成是独立的在一个等效势场中的运动，这个等效势场包括原子核的势场和其他电子对该电子的平均作用势（库仑势和交换相关势）。

3）周期性等效势场近似，把固体抽象成具有平移周期性的理想晶体，将固体中电子的运动归结为单电子在周期性势场中的运动。

固体能带计算就是求解对固体系统作了三个近似后得到的单电子方程，前边已经讲过，对这样一个单电子方程进行精确求解是不可能的，只能求近似解。固体能带计算方法很多，有平面波方法、紧束缚近似法、正交平面波法、赝势法、等等。这种采用从头计算法求解固体的单电子薛定谔方程或科恩-沈[吕九]方程得到能带E_n（k）和波函数的方法，称为第一性原理方法。值得注意的是，通过周期性势场的近似，固体已被近似成具有周期性结构的理想晶体，将固体能带计算转化为晶体能带计算。(https://www.xing528.com)

因为能带的计算与前面的内容有所重复，不再另作介绍，可参考前面的章节。

晶体能带及晶体物理性质的计算过程如图8-5所示，晶体是一个具有周期性结构的体系，输入时只能给出一个体积有限的晶体结构模型，需利用周期性边界条件，才能得到整个晶体的能带结构。

在选择了计算任务之后，需对计算参数进行设置，如自洽场计算的精度、基组的大小、k的取值等。自洽场计算的收敛用电子数密度或晶体总能量的收敛来标志，自洽场计算的精度是指收敛的标准。在晶体能带计算中，基组是指用于线性组合成单电子波函数的基函数集合，如平面波方法中的平面波、紧束缚近似方法中的原子轨道组合成的布洛赫（Bloch）函数。在平面波赝势方法中，给出能量的截断值，确定基组中平面波的数目。能带E_n（k）函数是k的准连续函数，k在k空间均匀分布，其取值限定在布里渊区中，k可以取大量的值。由于计算量的原因，计算时k只取简约布里渊区中有限的值。在其他条件不变的情况下，k的取值数目增加，得到的E_n（k）函数的精确度增大，但计算量显著增加。

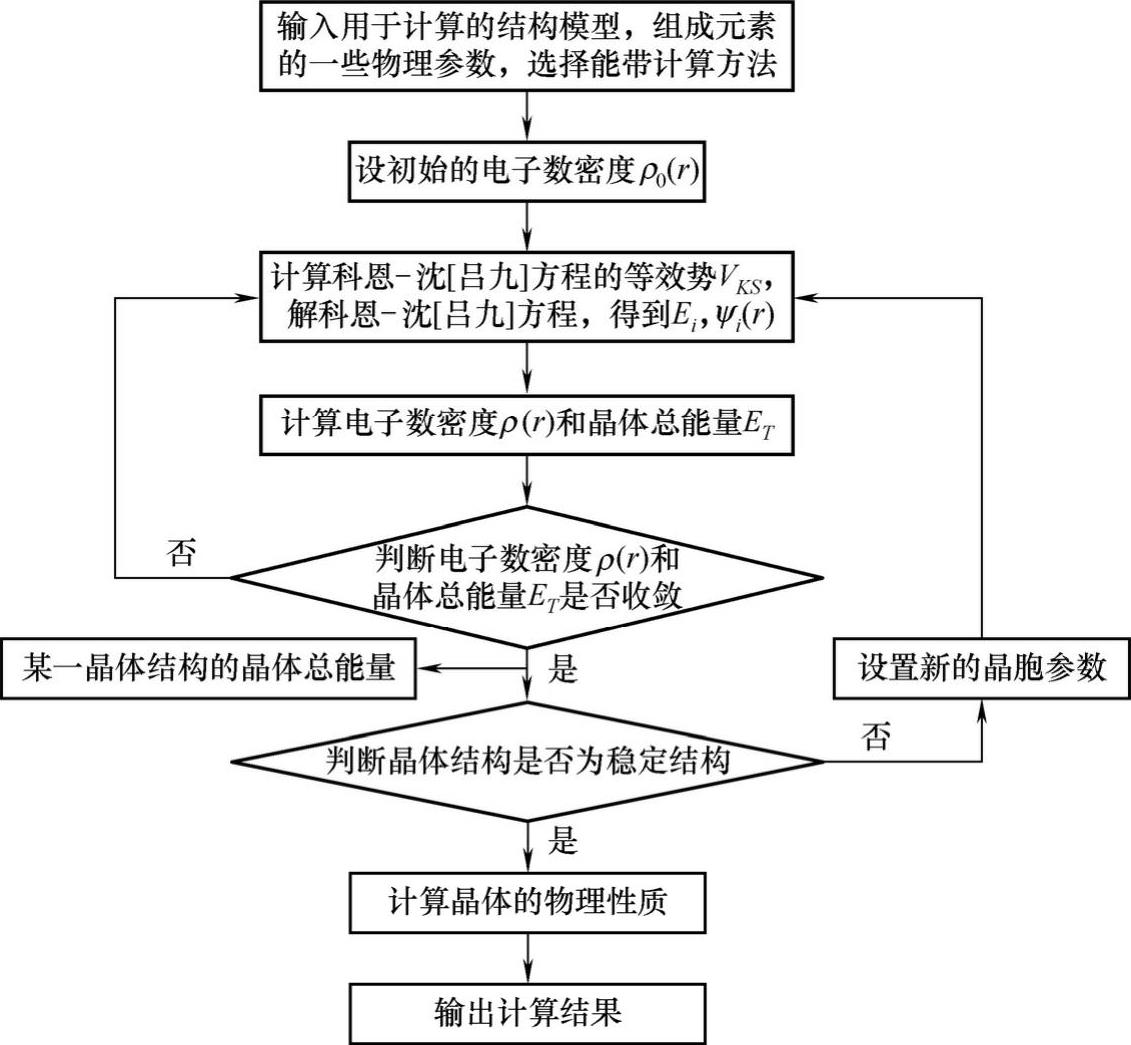
图8-5 晶体能带及晶体物理性质的计算过程