自洽场（SCF）计算优化

在实际的计算中，科恩-沈[吕九]方程是通过自洽计算来求解的，其计算流程如图8-4所示。图中的流程为：将多体系统原胞划分为足够细的网格点，在每个网格点上初始化一组试探波函数（通常设为随机数），然后算出网格上的科恩-沈[吕九]势，求解本征方程。解出来的本征函数的值与初始化的试探波函数的值一般不会相同，再将新解出来的波函数的一部分叠加到初始值上重新计算科恩-沈[吕九]势，利用修正过的势再次求解本征方程。所得到的本征函数又用于修正上一步循环输入的波函数……循环迭代的结果，是最终求得的本征函数的值不再变化，计算得以收敛。利用收敛后的这组单电子波函数，就可得到体系总能量和电荷密度分布。

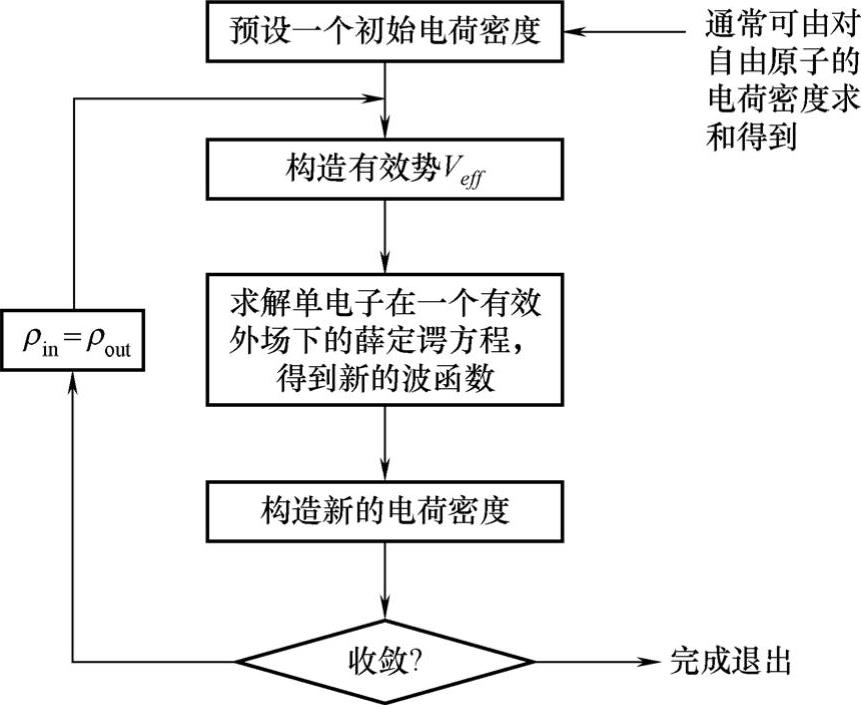
图8-4 自洽方法求解科恩-沈[吕九]方程流程图

1.求解单电子波函数

求解单电子波函数本质上是一个求本征值问题。对小矩阵，有很多数值算法可以直接求解。然而，电子结构计算中通常遇到的是很大的矩阵，无法直接对角化。当只对少数最低的本征值感兴趣时，可以用迭代算法求解。常见的迭代算法有，单带共轭梯度法、Davidson法与RMM-DIIS法以及Lanczos法，这里不再详细叙述，请参阅其他有关资料。

2.求电荷密度与能量

（1）分数占据（Partial Occupation）

在前面讨论布里渊区积分时，没有考虑占据数（零温下为阶梯函数）的影响。

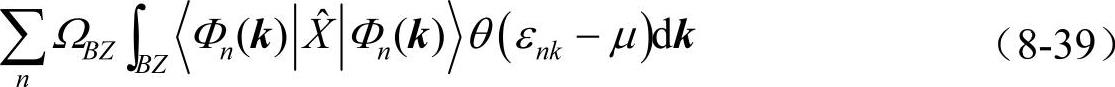
事实上，阶梯函数在数值上不稳定，使得布里渊区积分随k点数目收敛很慢。此时，常引入分数占据来代替阶梯函数。

1）费米-狄拉克Fermi-Dirac分布函数

优点：温度具有物理意义。

2）高斯（Gauss）型

优点：可以外推得到T=0时的能量。

3）Methfessel&Paxton方法。MP方法通过将阶梯函数用一组正交函数展开来实现，Gaussian函数是其零阶近似。因此，我们通常说的MP方法是指大于0阶的情形。对于合理的σ=k_BT的值，MP方法中F里的熵贡献较小，这样计算的力会更准。一个合理的判据是选择合适的σ，使得熵小于1meV/（atom·K）。MP方法的弱点是不适用于半导体或绝缘体，有可能出现占据数大于1的情况。

4）四面体（Tetrahedron）方法

数占据从算法上也可以看成对布里渊区积分离散化时，对不同k点的权重进行系统的调整。从这个思路出发，在由四个k点组成四面体内做线性插值可以得到修正的权重，也即等效的分数占据函数f_nk。实际应用上常采用Blochl等人提出的修正的四面体算法。

1）自动选择四面体使误差尽量抵消。(www.xing528.com)

2）对金属，误差抵消不完全，加入修正项。

3）最后积分形式仍为加权求和。

修正的四面体算法可以十分准确地计算能量、态密度等量，且不需要输入额外的参数。但是，由于它对分数占据不满足变分原理，所以得到的力可能不够准确，不能用来优化金属体系。

（2）能量泛函

在SCF迭代过程中，运用类似与热力学中的勒让德（Legendre）变换，能量泛函可以写成不同的形式。收敛以后它们都得到同一个能量，但是它们趋向于收敛的行为各不相同。KS能量泛函的原始定义为

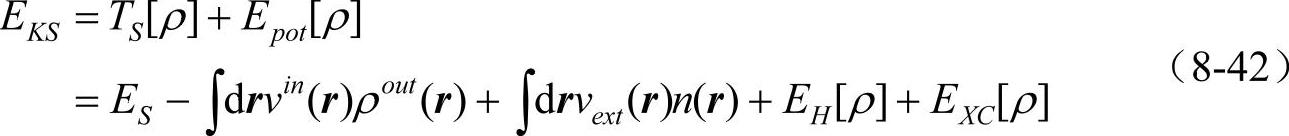
KS能量泛函原则上是电荷密度的泛函，但是在实际操作中可以看成有效势的泛函

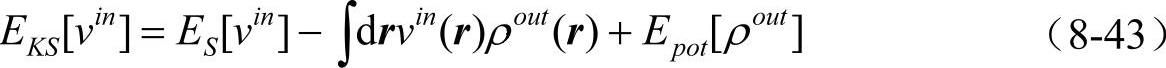
它满足变分原理。我们也选择另外一种显式的密度泛函形式，这就是常用的Harris-Foulkes（HF）泛函。因为输入势可以由输入密度决定，我们将v[ρⁱⁿ]记为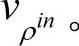

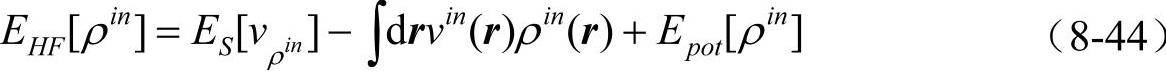
因为自洽收敛时ρⁱⁿ=ρ^out，HF泛函显然与KS泛函有同样的收敛性质。但是，HF泛函不满足变分原理，它主要用在非自洽计算（无需计算ρ^out）时的能量估计，而且在自洽计算的过程中HF泛函给出的能量值也通常比KS泛函更接近真实能量。

3.SCF迭代：mixing

SCF迭代刚开始时ρⁱⁿ和ρ^out可能会相差很大，使得整个算法不稳定，收敛困难。这时需要做一定的mixing。

（1）Linear mixing

为了考察的α取法，定义与真实密度的差为δρ=ρ-ρ_KS。在基态密度附近线性化，δρ^out=（χ～+1）δρⁱⁿ，若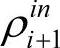=ρ_KS，则可收敛。可以证明，欲使SCF收敛，则有：。

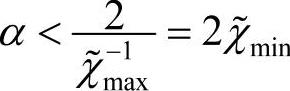从物理上来看，响应函数可以看成极化率的度量。所以，对束缚很强的刚性系统，可以取较大的α，而对于金属表面之类的较软的系统，则比较困难。

（2）其他Mixing算法

对介电函数作均匀电子气Thomas-Fermi屏蔽近似，可以得到Kerker Mixing，其形式与linear mixing基本相似，这里不作具体介绍。