波函数的展开原理及应用简析

在实际求解科恩-沈[吕九]方程时，由于原子核产生的势场项在原子中心是发散的，波函数变化剧烈，需要用大量的平面波展开，因而计算变得十分困难，所以需要尽可能包含少的基函数。好的基应该收敛快，计算中可以包含尽量少的维度。根据不同研究对象，有很多不同的选择基函数的方法，如原子轨道线性组合法（linear combination of atomic orbitals，LCAO）、平面波方法（plane wave，PW）、缀加平面波法（augmented plane wave，APW）、格林函数法（KKR）、线性缀加平面波法（linear augmented plane wave，LAPW）、Muffin-tin轨道线性组合法（linear muffin-tin orbitals，LMTO）等。

1.布里渊区积分

在通常的能带图中，经常会出现比如Γ、Λ、Κ、Χ、…符号。这些符号表示的是布里渊区内的高对称性的一些特殊的k点。这些k点有特殊重要的意义，是因为在进行体系总能计算时，通常要对布里渊区内的波函数或本征值进行积分，在实际计算过程中，积分是通过对部分特殊选取的k点的求和完成的。比较常见的k点网格的撒取方法有Monkhorst-Pack方法。

众所周知，根据布洛赫（Bloch）定理，周期体系中的电子波函数可以表述为调幅平面波的形式，即

ψ（k，r）=μ（r）exp（ik⋅r） （8-30）

其中，k是电子波矢，μ（r）是具有晶体平移周期性的周期函数。其本征能量和本征矢量为：En（k），Φn（k）。不同的电子状态按照量子数n进行分类，而量子数n则表征能态的分立性。研究多体体系的价电子问题，归根结底是计算出不同类的电子状态的本征值和本征矢量，体系处于基态情况下，哪些不同k的低能量状态被电子占据。因体系具有周期性，所以，第一布里渊区的所有k可以代表所有的k。但是，由周期边界条件确定的k有无穷多个，而且计及相互作用势的实际体系中许可的k在倒易空间内是不均匀的，实际计算过程中只能选取有限个点。

对周期性体系，电子结构计算与分析都涉及布里渊区（BZ）积分，通过玻恩-冯卡门边界条件，在实际计算中积分变成求和的形式。更一般地，积分可以变成对部分特殊选取的k点进行带权重的相加。这样，就涉及到k点的选取。在计算过程中，要用尽量少的k点得到尽可能精确的积分。对任意函数，如果取如上两个k点，可以保证其傅里叶展开以后直到2阶分量的积分为零。因此，为了获得较高的效率需要选取一些特殊的k点，原则是对一定的k点数量使得尽可能高的傅里叶分量的积分都为零。同时，k点的选取也需简便易行，综合考虑后较好的方法为Monkhorst-Pack（MP）取点法，它将三维问题转化为三个一维问题。一套MP网格是BZ内均匀分布的规则格点集，其数目由参数n_k1×n_k2×n_k3n决定。MP的k点的分数坐标取为u_r=（2r-n_k-1）2n_kr=1，2，3，…，n_k。

Monkhorst-Pack方法的k-grid对偶数分割不包括原点，这样可减少需要计算的点的数量，如图8-3所示。经验表明，对nk≤8，应尽量采取偶数分割，否则采取奇数分割。对六角晶格，因为晶格矢量不垂直，MP分数坐标公式需作一定的修正，此时应该将Γ点包含在k网格中。与绝缘体比较，金属需要更密的k点。

图8-3 Monkhorst-Pack方法的k点选择

a）含原点，需计算6个点； b）不含原点，只需计算3个点

2.平面波（PW）方法

平面波方法是以平面波为基函数展开电子波函数。这种方法的数学形式相当简单。在大多数情况下，哈密顿量矩阵元在平面波基下可以简单地用解析式表达，而且平面波基是非定域的，不依赖于原子的位置。但晶体的电子波函数占有很宽的动量范围，在靠近原子核的区域，电子动量很大，波函数快速振荡，在远离原子核的区域，电子动量很小，波函数变化平缓。因此，要准确地描述电子运动状态，波函数展开所需的平面波数相当大，使得计算量庞大。为克服这一困难，通常采用动量较小的平面波和具有较大动量的孤立原子芯态波函数构成正交化平面波，用正交化平面波为基函数展开电子波函数，只需要少数几项就可以很好地描述晶体中的电子运动状态。

平面波是最简单的正交完备基，根据布洛赫定理，单电子波函数可以用平面波展开

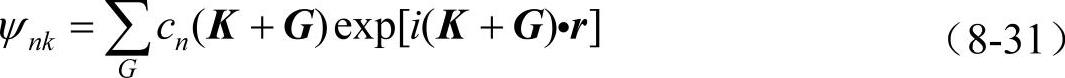
式中，G是原胞的倒格矢，K是第一布里渊区的波矢，c_n（K+G）是平面波展开系数（简称平面波系数）。在对真实系统的模拟中，由于电子数目的无限性，K矢量的个数从原则上讲应该是无限的。但由于ψ（r）随K点的变化在K点附近是可以忽略的，因此可以使用K点取样通过有限个K点进行计算。另一方面，为了得到对波函数的准确表示，G矢量的个数也应该是无限的。但由于对有限个数的G矢量求和已经能够达到足够的准确性，因此对G的求和可以截断成有限的，给定一个截止能

对G的求和可以限制在（G+K）≤E_cut的范围内，即要求用于展开的波函数的能量小于E_cut。当K=0时，即在Γ点，有很大的计算优势，因为这时波函数的相因子是任意的，就可以取实的单粒子轨道波函数。

哈密顿矩阵元为

(www.xing528.com)

原则上无穷多个平面波才构成一个完备集，但具有较小动能|K+G|²/2的平面波系数c_n（K+G）比具有较大动能的平面波系数大，因此可以只用小于某一能量E_cut的平面波作为基进行展开。E_cut越小，计算越容易，但截断所引起的误差也越大，因而需要增加E_cut直到收敛。

由于固体中离子实附近具有很强的局域势，在远离原子核处，波函数的行为趋近于一个平面波，但在近核处变化很快，全电子计算的平面波展开收敛太慢。众所周知，固体中许多物理性质主要由费米面附近的价电子决定，赝势方法利用这个性质，采用一个减弱的赝势来代替内层电子和原子核势场，相应的赝势作用下的波函数不再有振荡特征，而是平滑的赝波函，因此大大减少了平面波展开所需要的平面波函数目。

可将真实价波函数ψn（k，r）看做是由赝势波函数λ_n（k，r）和内层波函数φ_J（k，r）线性组合

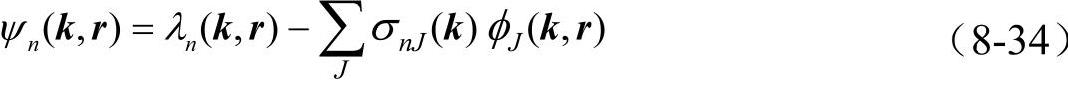
其中系数σ_nJ（k）由正交条件确定

联合真实波函数ψn（k，r）所满足的薛定谔方程[T+V（r）]ψ_n（k，r）=E_n（k）ψ_n（k，r），可得到赝波函数满足如下方程

上式中U_ps称为原子赝势。根据密度泛函理论，原子赝势包括离子赝势价电子库仑势和交换关联势：。其中后两项V_H^ps（r）和V_xc（r）可以从真实电荷密度计算（此时等于对应的全电子势V_H和V_xc），也可从赝电荷密度计算。

从上面可知：

1）赝波函数和真实波函数具有完全相同的能量本征值E_n[k]，这是赝势方法的重要特点。

2）赝势第二项是排斥势，与真实的吸引势有相消趋势，因此比真实势弱。

3）赝势包括局域项，其中非局域项同时与r和r'处的赝波函数λ_n（k，r）和λ_n （k，r'）有关，而且依赖于其能量本征值E_n（k）。

利用平面波基来计算有很多优点。首先平面波基能很方便地采用快速傅里叶变换（FFT）技术，使能量、力等的计算在实空间和倒空间快速转换，这样计算尽可能在方便的空间中进行。如前面讲到的哈密顿量中的动能项的矩阵元，在倒空间中只有对角元非零，就比实空间减少了工作量。第二，平面波基函数的具体形式并不依赖于核的坐标。这样，一方面，价电子对离子的作用力可以直接应用赫尔曼-费恩曼（Hellman-Feymann）定理得到解析表达式，计算显得非常方便。另一方面也使总能量的计算在不同的原子构型下有基本相同的精度。此外，平面波计算的收敛性和精确性比较容易控制，因为通过截断能E_cut的选择可以方便地改变平面波基的多少。当然平面波基也有缺点，一般电子轨道具有一定的局域性，而平面波是空间均匀的，因此电子轨道展开时与原子轨道基相比，平面波基的个数要多得多。为了尽量减少平面波基的个数，一般在平面波的计算中都采用赝势来描述离子实与价电子之间的相互作用，使电子轨道波函数在离子实内部的分布尽量平缓些。

3.LCAO方法

原子轨函线性组合（LCAO）方法的中心思想就是用原子轨道的线性组合来作为一组基函数，由此求解单电子薛定谔方程。这种方法在绝缘体的能带结构研究中是成功的。处于同一格点上的原子轨道是正交的，但不同格点上的原子轨道函数一般是非正交的，由它们组成的基函数也是非正交的，在计算中必然会遇到多中心积分的计算问题，计算量相当庞大。为了克服这些困难，人们提出了许多方案，如Slater-Koster参数方法和W.A.Harrison键轨道近似。

Slater-Koster参数方法将原子轨道线性组合方法中的哈密顿量矩阵元看成参数，其大小由布里渊区中心或边界上高对称性电子波矢的精确理论值或实验值拟合得到。一般来说Slater-Koster参数方法对半导体价带的描述较好，但对导带的描述却不太好。为了得到对价带和导带较好的描述，往往大量引入参数，有时参数达到50个之多。价键轨道近似在化学中应用广泛，但应用于固体时，由于忽略了成键态与反键态的耦合作用，在半导体中，对类s价带的描述较好，但对价带顶的类p价带的描述却不好，没有色散，反映在电子态密度上为一个δ函数。为改善对类p价带的描述，W.A.Harrison还引进了额外的相互作用参数。此外键轨道近似对导带的处理也不理想。

4.APW方法

缀加平面波方法和糕模（muffin-tin）轨道线性组合方法有一个共同特点，即它们都与糕模（muffin-tin）势有关。muffin-tin势将晶体空间分为两个区域：以每个原子为中心的muffin-tin球形区以及球外的球间区域。假定在球内muffin-tin势具有球对称性，球间区域则常取为常数势。muffin-tin势通常被用于金属与合金的电子结构计算。缀加平面波方法可以给出整个能带结构的很精确的结果，但由于要求解的久期方程是一个超越方程，计算量还是很大的。原子球近似下的muffin-tin轨道线性组合方法在对分子、以四面体结构结合的绝缘体和半导体的单电子能量和结合能计算中会出现严重误差。而对于这种方法加以非muffin-tin近似修正是十分复杂的。