赝势技术的应用和发展

在求解固体的单电子波动方程时，用假想的势能代替离子实内部的真实势能，若不改变电子的能量本征值及其在离子实之间区域的波函数，则这个假想的势能叫赝势。利用赝势求出的价电子波函数叫赝波函数，赝波函数所满足的波动方程

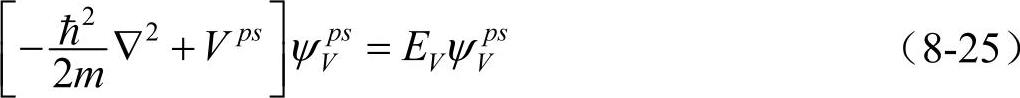
式（8-25）又称为赝势方程。方程中V^ps是赝势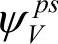，是价电子的赝波函数，E_V是价电子的能量。

在实际求解科恩-沈[吕九]方程时，由于原子核产生的势场项在原子中心处是发散的，波函数变化剧烈，需要用大量的平面波展开，因而计算变得十分困难。通常的做法是把空间区域按糕模（Muffin-tin）球划分，波函数在球内的部分由球面波展开，同时设定球外的原子势场为常数零。也可以用赝势方法，即把原子核的库仑吸引势加上一个短程的排斥势，两项之和（赝势）在原子核附近变得比较平坦，而得到的本征能量和价电子波函数与真实本征值及在原子核外的真实波函数是一样的。

赝势同时概括了离子实内部的吸引作用和波函数的正交要求，二者相消，如图8-1c所示，赝势比离子势弱，比较平坦。对于这样的赝势系统，用平面波展开赝波函数可以很快收敛。实际采用的赝势总是要使价电子波函数在离子实内部尽可能的平坦，且在离子实之间的区域给出与采用真实势相同的波函数，见图8-1d。值得指出的是，虽然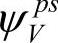是赝波函数，但由此得到的能量却是相应于晶体真实价电子波函数的本征能量E_V。

方程（8-25）中的赝势是有效势，它包含离子实的作用（称为离子赝势或原子赝势）和价电子的作用。在赝势方法中，使用的离子赝势（原子赝势）可分成三类：经验赝势（EPM）、半经验原子赝势和第一性原理从头计算原子赝势。

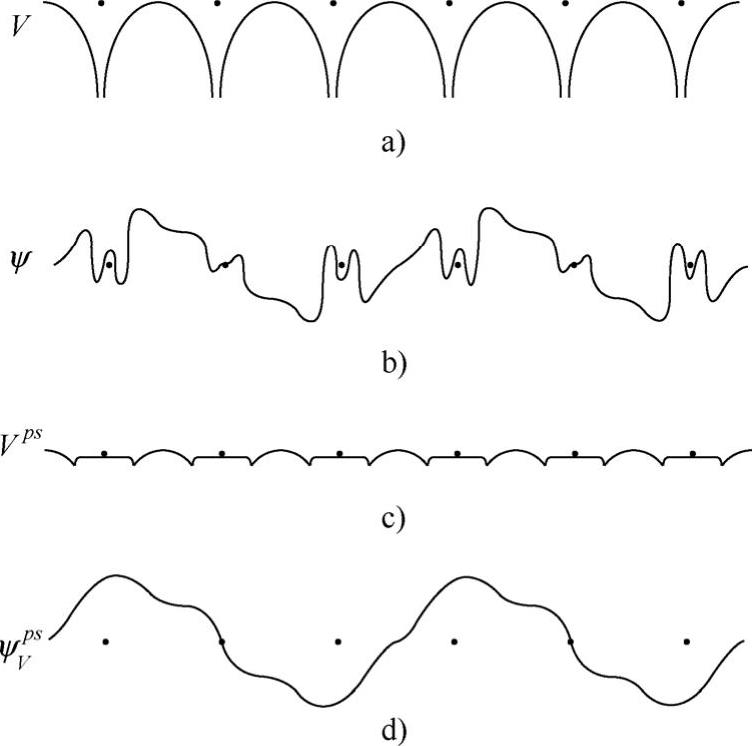
图8-1晶体周期势（图a）、Bloch波函数（图b）与赝势（图c）、赝波函数（图d）的比较

在经验赝势方法中，晶体势被表示成原子势的叠加，在赝势拟合过程中经过反复与实验数据（一般是能带、态密度、响应函数等）作比较、修改，直至得到与实验数据接近的结果。目前，经验赝势方法最主要的用途是在现代从头算原子赝势自洽迭代计算中做初始值使用。模型赝势是用于自洽计算的半经验原子赝势，在这种赝势表达式中含有一个或几个可变参量，用与实验数据相比较的办法来确定这些参量。没有任何附加经验参数的原子赝势，称为第一性原理从头算原子赝势。目前，在能带理论计算中最常用的从头算原子赝势是D.R.Hamann提出的模守恒赝势。

理论计算中最常用的赝势是模守恒赝势以及超软赝势，这些赝势所对应的波函数不仅与真实势对应的波函数具有同样的能量本征值，而且在r_c以外，与真实波函数的形状和幅度都相同，另外在r_c以内变化缓慢，没有大的动能。

在密度泛函理论的LDA和GGA的框架下，赝势的首要用途是在现代从头计算原子赝势自洽迭代计算中作初始值使用。这种赝势的最大优点是它的易于处理的简单形式，能以最小的代价用于任意晶体的能带计算。虽然这种经验赝势产生的电荷分布与真实的不完全一致，但它能正确地体现出晶体的对称性，在一个耗费很大的第一性原理赝势自洽从头计算中给出了一个很好的初始值。

赝势应用过程中的一个概念就是赝势的硬度。如果一个赝势使用很小的傅里叶格子就取得精确的结果，则称此种赝势为软的，反之则称之为硬的。现在在能带理论计算中最常用的Hamann等提出的模守恒赝势就是一种相当硬的质势。Vanderbilt所提出来的超软赝势的想法是不用释放非收敛性条件的，用这样的方法来产生更软的赝势。在这种方法里，虚波（seudo-wave）函数在核心范围被允许做成尽可能的软，以得到尽可能小的截止能量。从技术上而言，这是靠广义的正交条件来实现的。为了要得到总的电子密度，波函数平方所得到的电荷密度必须在核心范围内再加上附加额外的密度。这个电子云密度因此被分成两个部分，第一部分是一个延伸至整个单位晶胞的平滑部分，第二部分是一个局域化在核心区域的自旋部分。前面所提的附加部分只出现在密度里，并不出现在波函数中。超软赝势除了比模守恒赝势更软外，还有另外一个好处。采用超软赝势保证了在预先选择的能量范围内会有良好的散射性质，这使得产生的赝势具有更好的转换性和精确性。

1.模守恒赝势（norm conserving pseudopotential，NCPP）

除了经验势和可用于自洽计算的半经验模型赝势外，常用的第一性原理赝势方法为模守恒赝势。它要求赝势波函数满足如下条件。

1）本征值与真实本征值相等。

2）没有节点。

3）在原子核区之外（r>r_c）与真实波函数相等。

4）在内层区内（r<r_c）的赝电荷与真实电荷相等，将赝波函数插入到薛定谔方程中即得对应的赝势。一般说来，小的r_c移植性好，可用于不同环境，但平面波收敛慢。(www.xing528.com)

模守恒赝势产生的基本思想是对于孤立原子，构造一个参数化的等效势V，在给定交换关联模型的条件下，求解的单电子方程得到赝波函数φps和本征值；在相同交换关联模型下求解全电子方程，得到波函数ψ和本征值。调整参数化势能函数U，使得到的两组本征值相同，在某个截断半径r_c以外波函数一致，在该截断半径以内保证波函数的模方一致，此时的等效势V有效地描述了价电子感觉到的来自原子核和处于稳定状态的满壳层电子的相互作用，这个等效势就是模守恒赝势U_ps。赝势的构造有可能将波函数急剧振荡的芯区用一个平滑的波函数替代而不改变电荷密度分布。平滑的波函数在用平面波展开过程中需要的平面波矢要小得多，在晶体环境中，这意味着截断能的降低，进而导致收敛性的改善。

第一性原理模守恒赝势可分为局域和非局域两部分

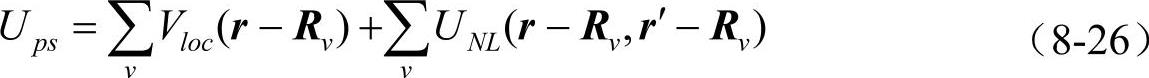
其中，v是对离子势求和。考虑到原子球对称性，得用球谐函数将赝势的非局域部分写成

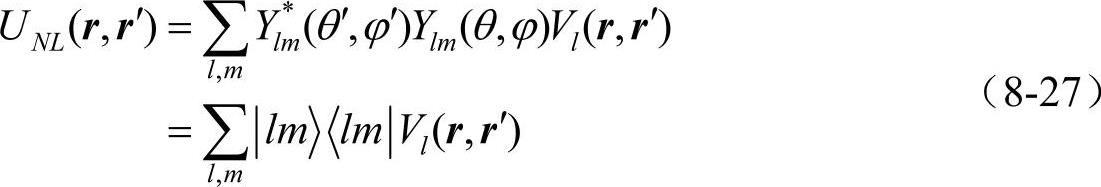
如果将V_l（r，r′）取成半局域形式，即径向是局域的，只有角部分是非局域的：V_l（r，r′）=V_l（r）δ（r，r′），并定义角动量l的投影算符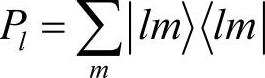。则半局域的原子赝势可以写成如下的形式

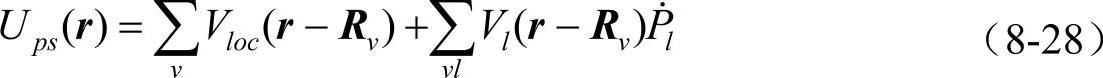
为了简化计算，Kleinman和Bylander（KB）将上面半局域赝势部分用一个非局域赝势来近似

模守恒赝势方法可以在局域密度近似下采用平面波基精确有效地计算固态性质，且可移植性好，但在描述局域价轨平面波基仍然很大，因而在第Ⅰ族元素和过渡金属中的应用受到了限制，通过优化光滑的赝波函数或赝势和增大截断半径rc的改进有一定效果，但模守恒条件的限制使得在一些情况下，如O2p或Ni3d轨道，很难构造出比全电子波函数更光滑的赝波函数，收敛仍然很慢。

模守恒型的赝势从最早的Hamann等提出，后来建立一组涵盖整个周期表的参数，之后的Kerker、TM赝势，一直到Optimised赝势，都是在朝着兼顾准确性的情况下，尽可能使必须使用的平面波基底数目越少越好，它是直接影响着所需计算量大小的量。一个赝势所需的基底数多少，可由系统总能E_tot对截断动能E_cut的收敛性来判断，即平面波截断动能E_cut用到多大时则固态计算所求得系统总能就不再改变，所需E_cut越小，也就是所谓的赝势越“软”。

使用Optimised或TM赝势虽然能够把模守恒型赝势变得很“软”，但模守恒条件对于原本就已经没有节点价电子云分布的改造及最佳化的程度，与现今日渐普遍的超软赝势（它不必遵守模守恒条件）来比，节省计算的程度仍是有限的。总之，计算量的大小是取决于原子的种类这一点，是十分明确而普遍的认识，也就是说不同种类元素其势的“软硬”差异会令人明显感觉到。

2.超软赝势（ultrasoft pseudopotential，USPP）

事实上，模守恒条件并不是必须的，任何构造一套光滑的赝波函数，只要它能够通过某种方式从赝波函数得到真实的电荷密度，将之插入到具有正确本征值的径向薛定谔方程中得到相应赝势，就能实现计算目的。在此前提下，收敛越快的越好。Vauderbilt提出的超软赝势方法，它是通过对模守恒条件的弛豫而发展了的一套方法。超软赝势的赝波函数已经不必再遵守模守恒条件，而是通过定义附加电荷来达到所谓的模守恒条件的，其目的基本上是将被砍掉的较局域化的电子云补回去。它构造的赝波函数在内层区之外（r>r_c）和全电子波函数一致，而在内层区内（r<r_c），通过引入一个广义的正交条件，用于自洽计算的真实电荷密度可以从赝波函数计算得到。图8-2给出了氧原子2p径向波函数、模守恒赝波函数和超软赝波函数的比较。

超软赝势目前已经成功地应用于过渡金属和第Ⅰ族元素计算中。

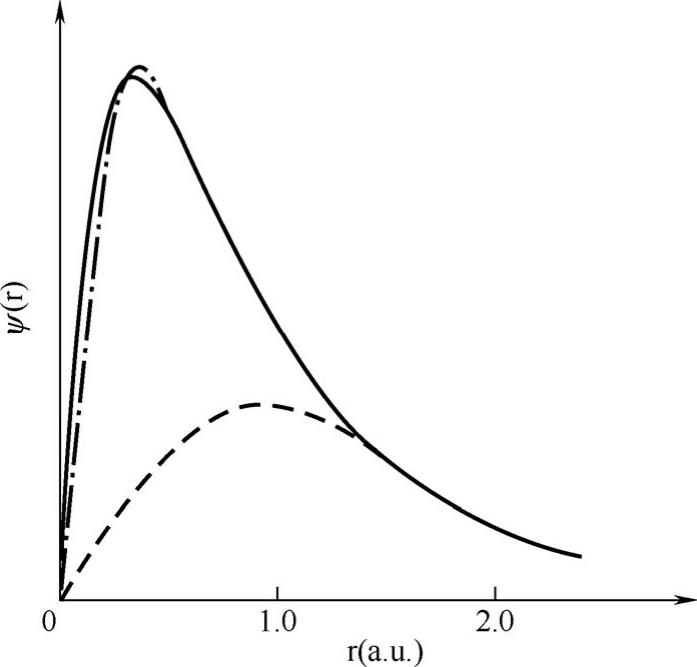
图8-2 氧原子2p径向波函数（实线）、模守恒赝波函数（点画线）、超软赝波函数（虚线）的比较