交换关联能泛函简介

在整个密度泛函的理论中，由于交换关联能泛函E_xc[ρ（r）]是未知的，具体计算中需要作适当的近似。显然密度泛函计算结果的精度，取决于交换关联势质量的好坏。

1.局域密度近似（Local Density Approximation，LDA）

局域密度近似是实用中最简单有效的近似。它最早由Slater在1951年提出并应用，甚至早于密度泛函理论。这种近似假定某处的交换关联能只与该处的密度有关，且等于同密度的均匀电子气的交换关联能，因此可以把交换关联能近似写为

其中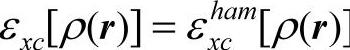，，是每个电子在密度为ρ（r）的均匀电子气中的交换能和关联能之和。则交换关联势为

如果考虑自旋不同的电子的密度ρ（r）和轨道也不相同，相应的LDA就称为LSDA或者LSD。

LDA近似在大多数的材料计算中展示了巨大的成功。经验显示，LDA计算原子游离能、分子解理能误差在10%～20%；对分子键长、晶体结构可到1%左右。

但是，局域密度泛函近似认为交换关联能函数完全是局域的，原则上忽略了某一点r附近电荷密度的非均匀性所带来的影响。虽然对于均匀电子气的交换关联能的计算结果较准确，但是对于与均匀电子气或者空间缓慢变化的电子气相差太远的系统，也就是在一些能量梯度很高的情况下，如方向性的成键，LDA就难以得到精确的结果，往往过高估计键能。此外，分子的离解能和固体中的内聚能也常常被高估，虽然这种误差通常可在接受的精度范围内。因此对LDA需加以改进，使其适应性和精度提高。

2.广义梯度近似（GGA）

迄今为止，已有数种尝试改进LDA的方案。其中较为成功的是广义梯度近似（GGA）。在GGA近似下，交换相关能是电子（极化）密度及其梯度的泛函。构造GGA交换相关泛函的方法分为两个流派。以Becke为首的流派认为“一切都是合法的”，所以人们可以以任何原因选择任何可能的泛函形式，而这种形式的好坏由实际计算来决定。通常，这样的泛函的参数由拟合大量的计算数据得到；以Perdew为首的流派主张尽量少引入拟合参数，通过渐进行为等物理限制来得到较好的泛函形式。基于这种理念构造的一个著名的GGA泛函是PBE泛函，也是现在用得最广泛的GGA泛函之一。除了密度梯度以外，在泛函中包含其他自变量（如动能密度）而得到的泛函称为meta-GGA。泛函不同的LDA方案之间大同小异，但不同的GGA方案可能给出完全不同的结果。(www.xing528.com)

GGA的交换-关联能表达式与LDA类似，只是在其ε_xc[ρ（r）]中加入了电子密度梯度，如

由于加入了一个非局域梯度项，GGA从原理上来说应该更适合于处理非均匀体系。事实上，与LDA比较，GGA只改进了原子交换关联能的计算，对价电子的电离能仅有小的变化。分子中的键长和固体中的晶格常数稍有增加，离解能和内聚能明显下降。然而至少对于较轻的元素，GGA的结果一般与实验符合得很好，不仅是其价键和金属键，氢键和范德华键的键能计算都得到了改善。

应该指出的是，GGA并非总是优于LDA。例如，对于4d过渡金属的晶格常数和内聚能，GGA的结果常常偏大，反不如LDA给出的精确。因此，很难说GGA与LDA谁更优越，只能由实际体系和计算的物理量来决定。由于GGA的计算量要高于LDA，迄今为止LDA仍是使用最为广泛的交换关联能近似。

需要注意的是，如果交换关联能泛函显式包含轨道时，我们无法直接计算泛函微分，通常需要一种非直接的方法来求泛函极值。

3.杂化密度泛函

哈特里-福克（Hartree-Fock）理论包含精确的交换关联能。因此，在DFT混合部分哈特里-福克交换可能有助于提高精度。通常，从科恩-沈[吕九]轨道得到的哈特里-福克交换被另外称为精确交换。最简单的杂化泛函可以写成

一个比较实用的杂化泛函是B3LYP

杂化密度泛函在分子体系中被广泛应用，但较少应用到固体体系，因为固态计算中流行的平面波基组方法实现精确交换的效率太低。