密度泛函理论（DFT）的原理及应用

20世纪60年代，Hohenberg、Kohn和Sham（沈吕九）提出了密度泛函理论，简称DFT。密度泛函理论将多电子波函数和薛定谔方程用简单的电荷密度ρ（r）和相应的计算方案来代替，不但给出了将多电子体系简化为单电子问题的理论基础，同时也成为当今分子和固体电子结构和总能量计算的有力工具。因此，密度泛函理论是多粒子系统理论基态研究的重要方法。DFT同分子动力学方法相结合，在材料设计、合成、模拟计算和评价等许多方面有明显的进展，成为计算材料科学的重要基础和核心技术。近年来，用DFT的工作以指数规律增加，现在已经大大超过用HF方法研究的工作。DFT适应于大量不同类型的应用，因为电子基态能量与原子核位置之间的关系可以用来确定分子或晶体的结构，而当原子不在它的平衡位置时，DFT可以给出作用在原子核位置上的力。因此，DFT可以解决原子分子物理中的许多问题，如电离势的计算、振动谱研究、化学反应问题、生物分子的结构和催化活性位置的特性、等等。在凝聚态物理中，如材料电子结构和几何结构、固体和液态金属中的相变等。DFT的另一个优点是，它提供了第一性原理或从头算的计算框架，在这个框架下可以发展各式各样的能带计算方法。下面对密度泛函理论进行介绍。

1.霍恩伯格-科恩（Hohenberg-Kohn）定理

1927年，H.Thomas和Fermi各自提出以电子密度的函数来表示能量的理论，这样当然大大减少了计算中的变量，但是由于缺乏对动能项的精确处理，这个早期的理论有点粗糙，主要侧重于化学方面，甚至有时会给出分子不会形成键结的计算结果，这个结论阻碍了托马斯-费米（Thomas-Fermi）理论的进一步发展。到了20世纪60年代，从电子密度出发的概念给出了Kohn新的想法，1964年Hohenberg和Kohn发表了后来极著名的霍恩伯格-科恩（Hohenberg-Kohn，HK）定理，对于无简并的基态：

定理一：不计自旋的全同费米子系统的基态能量是粒子数密度ρ（r）函数的唯一泛函（除了一附加常数外）。

定理二：能量泛函E[ρ]在粒子数保持不变的条件下对正的粒子数密度函数取极小值，并等于基态能量E₀，即在条件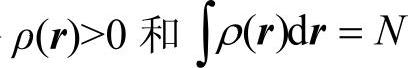下，满足δE[ρ]=0时的ρ为基态密度泛函，此时的能量等于基态能量E₀。

这两个定理统称为霍恩伯格-科恩定理。定理一说明，粒子数密度函数是确定多粒子系统基态物理性质的基本变量，多粒子系统的所有基态物理性质，如能量、波函数以及所有算符的期待值，都由粒子数密度函数唯一确定。定理二表明，如果得到了基态粒子数密度函数，就能确定能量泛函的极小值，并且这个极小值等于基态的能量，因此，能量泛函对粒子数密度的变分是确定系统基态的途径。

对于给定的局域势v（r）（表示外场的作用），多电子系统的能量是电子数密度（也称为电荷密度）ρ（r）的泛函，则对应的多电子系统的能量泛函E[ρ]为

式中，F[ρ]是与外场无关的泛函，它包括电子的动能和电子之间的相互作用能

E_ext[ρ]是局域势v（r）所表示的外场对电子的作用能

E_N-N是原子核之间的排斥能

为了说明F[ρ]，在式（8-12）中将F[ρ]分为三项，第一项和第二项是与无相互作用粒子模型对应的动能和库仑排斥能，第三项E_xc[ρ]代表了所有未包含在无相互作用粒子模型中的相互作用能。这里所谓无相互作用是指一个电子的存在对其他电子没有影响，而实际上一个电子的存在对其他电子是有影响的。如果在r处存在一个电子，那么在r'处的电子数密度将不再是r处无电子时的ρ（r），这表明电子间除了库仑排斥作用还存在其他的相互作用，这种相互作用包括自旋平行电子间的交换相互作用和自旋反平行电子间的关联相互作用。因此，E_xc[ρ]称为交换关联相互作用能（简称交换关联能），它包含了电子间相互作用的全部复杂性。E_xc[ρ]也是电子数密度ρ的泛函，可分成交换能E_x[ρ]和关联能E_c[ρ]两部分，即E_xc[ρ]=E_x[ρ]+E_c[ρ]。

根据霍恩伯格-科恩定理，如果能得到能量泛函E[ρ]，将E[ρ]对电子数密度ρ变分，就可以确定系统的基态和所有的基态性质。但要得到能量泛函E[ρ]，必须解决以下三个问题：

1）粒子数密度函数ρ（r）的确定。

2）动能泛函T[ρ]的确定。

3）交换关联泛函E_xc[ρ]的确定。

W.Kohn和L.J.Sham（沈吕九）提出了解决第一和第二个问题的方法，并由此得到了Kohn-Sham方程。对于第三个问题，一般采用局域密度近似来解决。

2.科恩-沈[吕九]（Kohn-Sham）方程(www.xing528.com)

上述霍恩伯格-科恩定理说明了电荷密度是确定多电子体系基态物理性质的基本变量，能量泛函对电荷密度函数的变分是确定系统的途径，但由于多电子体系中电子间的相互作用，严格确定相互作用系统的密度泛函E_xc[ρ]非常困难。

由于对有相互作用电子系统的动能项一无所知，W.Kohn和L.J.Sham提出：

1）假定动能泛函T[ρ]可用一个已知的无相互作用电子系统的动能泛函T_S[ρ]来代替，这个无相互作用电子系统与有相互作用电子系统具有相同的密度函数。

2）用N个单电子波函数Φ_i（r）构成密度函数ρ（r）

根据霍恩伯格-科恩定理一，如果ρ（r）确定，V_S（r）就唯一确定，因此无相互作用多粒子体系的能量也是ρ（r）的单值函数

其中，T_S[ρ（r）]是无相互作用多粒子体系的动能泛函

将能量泛函E[ρ]对ρ的变分用对Φ_i（r）的变分代替，以ε_i为拉格朗日乘子，变分后得到

其中，

这样，对于单粒子波函数Φ_i（r），也得到了与哈特里-福克方程相似的单电子方程，它包括局域势v（r）、库仑排斥势V_coul[ρ（r）]和交换关联势V_xc[ρ（r）]。式（8-15）、式（8-18）和式（8-19）一起成为科恩-沈[吕九]方程。现在，基态的电子数密度函数可由解方程（8-18）得到的Φ_i（r）按式（8-15）构成。根据霍恩伯格-科恩定理，这样得到的电子数密度可精确地确定该系统基态的能量、波函数及各物理量的期待值

科恩-沈[吕九]方程的核心是，用无相互作用电子系统的动能代替有相互作用粒子系统的动能，而将有相互作用电子系统的全部复杂性归入交换关联相互作用泛函E_xc[ρ（r）]中，从而导出形如式（8-18）的单电子方程。与哈特里-福克方程相比，密度泛函理论导出的单电子科恩-沈[吕九]方程是严格的，因为哈特里-福克方程只包含电子的交换相互作用，不包含电子的关联相互作用，而科恩-沈[吕九]方程不仅包含电子的交换相互作用，而且包含电子的关联相互作用。

在密度泛函理论中，利用科恩-沈[吕九]方程可将多电子系统的基态特性问题转化成等效的单电子问题，这种计算方法与哈特里-福克自洽场近似法相似，但其结果更精确。然而，遗憾的是归纳了所有复杂相互作用的交换关联能泛函E_xc[ρ（r）]是未知的，只有得到准确的、便于表达的E_xc[ρ（r）]，才能求解科恩-沈[吕九]方程。科恩-沈[吕九]方程主要有以下几个特点。

1）通过引入N个单电子波函数，严格计算出了动能的主要部分，代价是需要求解N个方程。

2）除了更一般的局域势外，科恩-沈[吕九]方程与哈特里方程具有相似的形式，求解两种方程的计算量也相差不大，但比求解具有非定域势的HF方程要简单。

3）尽管哈特里（Hartree）、哈特里-福克（Hartree-Fock）和科恩-沈[吕九]方程都提供了一个多电子体系的单电子方法，但三者具有本质的差别，前两者一开始就引入了近似，而科恩-沈[吕九]原则是严格的，它可由变分原理严格推导。

至此，利用密度泛函理论计算多电子系统总能和电荷密度空间分布的方案可以付诸实施了。