铁磁体中的畴壁及其能量密度

磁畴和磁畴之间的边界称为畴壁。在畴壁内原子磁矩的方向逐渐转变。根据原子磁矩转变的方式，可将畴壁分为布洛赫壁（Bloch Walls）和奈尔壁（Neel Wall），如图7-18所示。布洛赫壁的特点是畴壁内的磁矩方向改变时始终与畴壁平面平行，一般在大块的铁磁性材料内存在布洛赫壁。当铁磁体厚度减少到相当于二维的情况，即厚度为1～10nm的薄膜时，则畴壁的磁矩始终与薄膜表面平行地转变，这种畴壁称奈尔壁。由于畴壁内部的原子磁矩不再相互平行，磁矩间的交换作用能就有所提高，同时，由于在畴内磁矩偏离了易磁化方向，磁各向异性能也有所提高。因此，和磁畴内比，畴壁是高能区域。

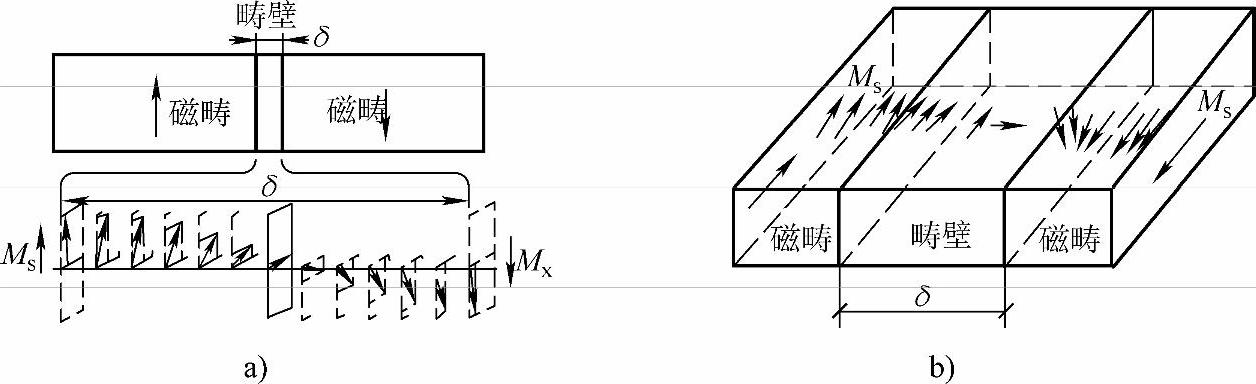
图7-18 布洛赫壁和奈尔壁中磁矩过渡的方式

a）布洛赫壁中磁矩过渡的方式 b）奈尔壁中磁矩过渡的方式

1932年布洛赫首先从能量的观点分析了180°布洛赫壁。如果原子磁矩在相邻两原子间突然反向，则交换作用能的改变ΔE_ex为

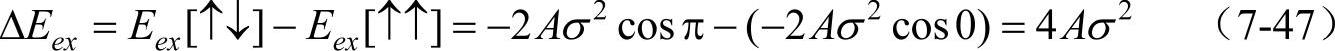
式中，E_ex为两原子自旋交换能；σ是电子以ћ为单位的电子自旋角动量；A为交换积分。但是如果在n个等距的原子面间逐步地均匀转向，如图7-18a所示，相邻两个原子之间的交换作用能E_ex（φ）则可以写成

式中，φ为相邻两个原子磁矩间的夹角，φ=π/n。当φ很小时，cosφ≈1-φ²/2。这时相邻两原子自旋的交换能的变化（ΔE_ex）_φ为

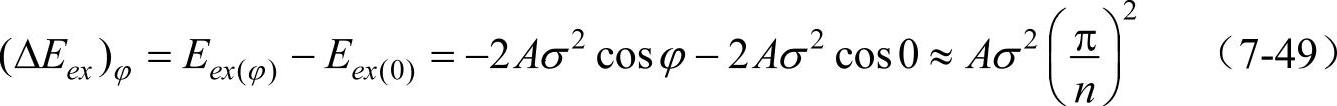(www.xing528.com)

在n+1个自旋磁矩的转向中，交换能的总变化ΔE_ex为

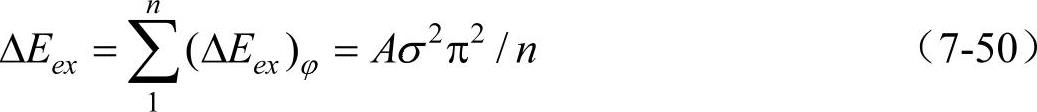
比较式（7-47）和式（7-50），后一种情况比前一种情况的交换能低得多。因此，畴壁中的原子磁矩必然是逐步转向。畴壁是原子磁矩由一个磁畴的方向逐步转向相邻磁畴的方向的过渡区。在畴壁内的交换能、磁晶各向异性能和磁弹性能都可能比磁畴内高，所高出的部分的能量称畴壁能，用Eω表示。畴壁单位面积的能量称畴壁能密度，用γω表示。由式（7-50）可知，如果只考虑交换能，则在畴壁内相邻原子磁矩的方向改变越小，交换能越小，即交换能使畴壁无限加宽。但是事实上这是不可能的。因为n越大，就有更多的原子磁矩偏离易磁化方向，使磁晶各向异性能增加。磁晶各向异性能力图使畴壁变薄。综合考虑以上两个方面的因素，使总能量为最小，可以求出畴壁能密度γω和畴壁厚度δ为

式中，A₁=Aσ²/a，a为点阵常数；K₁为磁晶各向异性常数。考虑当材料内部存在内应力时，由于应力也要引起应力各向异性，根据式（7-46），可以将应力各向异性和磁晶各向异性同样考虑，求得总能量最小时的畴壁能密度γ_ω和畴壁厚度δ分别为

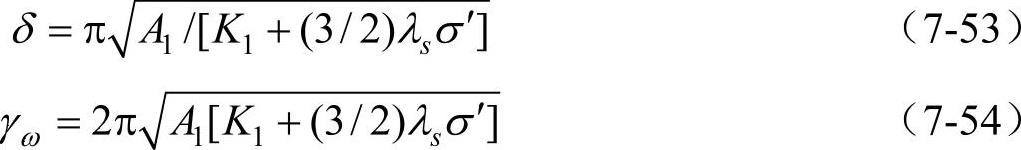
这里，λ_s为饱和磁致伸缩系数；σ′为内应力。

可见畴壁厚度与材料的K₁、A₁、λ_s、σ′等参量有关。K₁越大，δ越小，γ_ω越大。在Fe-Ni合金中，K₁很小，如果内应力也很小的话，则畴壁厚度可相当得大，这时畴壁内相邻原子间磁矩的角度φ仅有0.18°～1.8°，磁矩的分布近似具有连续性，这种畴壁称为连续性的畴壁模型。在六方结构的Co和SmCo₅等金属与合金中，由于K₁很大，δ很小，γ_ω很大。其φ角可达6°～180°，并且φ角的分布是不均匀的。这种畴壁称为非连续畴壁模型。窄畴壁对材料磁特性有重要的影响。