直接交换的作用

根据式（7-28）和式（7-31）估算一下分子场的大小。对于铁来说，T_c=1043K，n=8.49×10²⁸m^-3。设J（J+1）g_Jμ_B≈n_effμ_B=2.2×9.273×10^-24=2.04×10^-23A·m²（n_eff为原子磁矩的实验值），代入式（7-31）得λ=9.73×10²，铁的M_s=n_effnμ_B≈1.73×10⁶A·m^-1，代入式（7-28）得分子场约1.73×10⁹A·m^-1。这一磁场比晶体中一个原子磁矩在相邻原子处产生的磁场8×10⁵A·m^-1大3～4个数量级，说明分子场不起源于磁的相互作用。

当1924～1926年建立了描述微观电子运动的量子力学理论后，1928年海森堡（W.Heisenberg）和弗伦克尔（Фpeкeлъ）几乎同时分别提出分子场是相邻原子间电子自旋的交换作用的理论。这种交换作用是一种量子力学效应，是属于静电性质的。下面用氢分子模型说明交换作用原理。

图7-6 氢分子模型

图7-6中a、b分别代表两个氢原子核，l和2代表两个电子。在氢分子内原子核之间，原子核与电子间的距离分别如图7-6所示。当两个氢原子相距很远时，两原子的电子云不重叠，它们有各自能量E₀，两个孤立的氢原子的能量和为2E₀，同时两个氢原子间的电子自旋运动也相互不影响。当两个氢原子靠近到能形成氢分子时，两个氢原子就要结合在一起。这时电子的运动与两个孤立氢原子时的运动就不同了，相应地整个氢分子的能量与两个孤立原子的能量和也不同了。原子磁矩间磁的相互作用很弱不予考虑，而电的作用有如下几项：原子核之间的静电相互作用；l和2两个电子间的电相互作用；a核与电子1、2之间的电相互作用；b核与电子1、2之间的电相互作用。两孤立的氢原子结合成分子后，其能量为E=2E₀+E′。根据量子力学的理论计算，E′不仅决定于上述的静电作用，还与两个电子间自旋的相对取向有关。由量子力学的理论计算得到氢分子的能量为

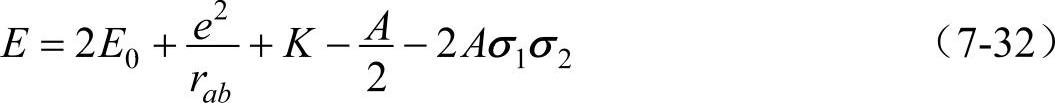
式中，K和A为

式中，ψa（1）和ψa（2）分别代表电子1和电子2在a核周围运动的波函数。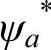（1）和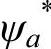（2）分别是它们对应波函数的共轭波函数。ψb（1）和ψb（2）分别代表电子l和电子2在b核周围运动的波函数。（1）和（2）分别是它们相应的共轭波函数。dτ₁和dτ₂分别代表空间的体积元。K是库仑相互作用的平均势能，它与两个电子之间的自旋取向无关。A是交换积分常数。在A项内包括了ψ_a（2）和ψ_b（1）的波函数，它代表电子1和电子2相互交换位置时对应的能量。A的大小与两电子云重叠的程度有关。

-2Aσ₁σ₂项是与两个电子自旋取向有关的能量，称为自旋交换能，用E_ex表示。式中σ₁和σ₂是两电子以ћ为单位的电子自旋角动量，即，Ps为自旋角动量。感兴趣的是两个电子自旋相对取向对能量的影响，因此把式（7-32）中的前四项能量看作是常数，而仅研究最后一项能量，即(www.xing528.com)

E_ex=-2Aσ₁σ₂ （7-34）为简便起见，把式（7-34）按经典矢量模型来处理，设两个电子自旋角动量矢量σ₁和σ₂的夹角为φ，这样可把式（7-34）写成

E_ex=-2Aσ₁σ₂cosϕ （7-35）可见当交换积分A为正时，交换能为最小值的条件是相邻原子间的电子自旋角动量同向平行排列（φ=0°，cosφ=1）。当交换积分A为负时，交换能最小的条件是相邻原子的电子自旋角动量反向平行排列（φ=180°，cosφ=-1）。

根据能量最小值的原理可得，当铁磁物质内部相邻原子的电子交换积分A取正值时，相邻原子自旋磁矩要同向平行排列，从而实现自发磁化到饱和。这就是铁磁性的起因。

原子磁矩不为零，交换积分常数A>0是铁磁性的必要与充分条件。由式（7-33）可知，相邻原子的电子云（波函数）在重叠区有相同符号，所以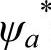（1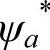）、（2）和ψa（²）、ψb（1）都是正的，要想使A>0，必须满足

可见要使A>0，必须要求r₁₂要足够小，即要求未填满的次电子层的电子云在两原子核之间重叠。不过重叠区也不能过分大。3d金属Fe、Co和Ni及它们的合金正好符合这一条件。因为3d电子的轨道角量子数l=2，其轨道半径较小，两电子云既重叠，但重叠区又不过分大，保证了A>0，因此它们是铁磁性的。根据这些条件，斯莱特（Slater）总结出交换积分常数A和a/r_3d的关系，如图7-7所示。a是相邻原子间距，r_3d是未填满电子的3d电子层的半径。当a/r_3d>3时，A>0，为铁磁性。但a也不能过大。若a过大，3d电子云不重叠，交换作用很弱，使A→0，为顺磁性。若a过小，就会使得式（7-36）不成立，从而使得A<0，导致反铁磁性。在Mn和Cr中通过添加第二或第三组元，扩大a值则有可能使反铁磁性转变为铁磁性。

图7-7 交换积分A和a/r_3d的关系