固体电介质热击穿判据及机制分析

当固体电介质在电场作用下，由电导和介质损耗产生的热量超过试样通过传导、对流和辐射所能散发的热量时，试样中的热平衡就被破坏，试样温度不断上升，最终造成介质永久性的热破坏，这就是热击穿。显然，热击穿除与所加电压的大小、类型、频率和介质的电导、损耗有关外，还与材料的热传导、热辐射以及试样的形状、散热情况，周围媒质温度等等一系列因素有关。

为了定量地研究介质在什么条件下发生热击穿，即要获得热击穿判据，首先要建立介质在电场作用下的发热或散热的临界平衡方程，从而得到在各项条件下的热击穿电压。在电场作用下，如试样的发热功率为W₁，散热功率为W₂，临界热平衡方程为W₁（T_m）=W₂（T_m），其中，T_m为介质达到临界热平衡时的最高极限温度，与T_m相应的电压就是热击穿电压。实际上要建立临界热平衡解析式是相当复杂的，现仅以一种最简单的情况为例加以说明。

设对面积为A、厚度为d的试样施加直流电压V，且介质只有漏导电流产生的热量。这时介质的电导率为σ，则试样的电导G=σA/d，这时介质的发热功率W₁=GV²。介质的电导率σ随温度T的上升指数式增加，其关系式可表示为σ=A′exp（-B/T），A′、B为常数。则

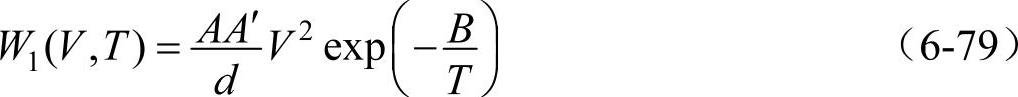
上式表明，W₁是电压V和介质温度T的函数，并随温度T增加指数上升。图6-16表示出了在不同的电压V₁、V₂、V₃下，W₁与T关系的曲线。

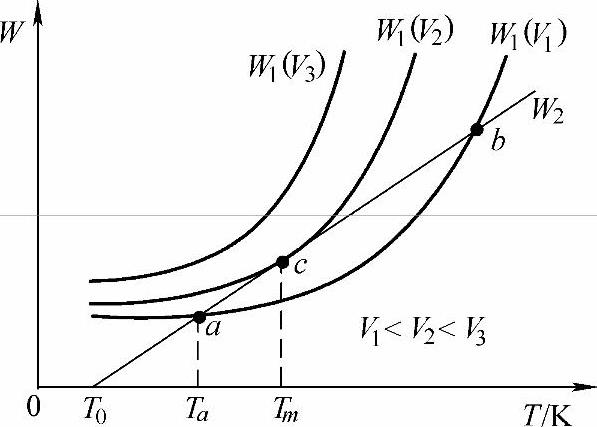
图6-16 在电压作用下固体电介质的发热与散热曲线

介质中所产生的热量，一方面使试样本身的温度升高，另一方面通过热传导和热对流向周围散发热量。如环境温度为T₀，散热功率W₂与温差T-T₀成正比，则(www.xing528.com)

式中，B′为与热传导和热对流有关的散热系数，可以把B′看成是一个与温度无关的常数。由上式可见，散热功率W₂与介质温度T呈线性，如图6-16所示。

由图6-16可见：①当外加电压V_l较小时，发热曲线W₁（V₁）与散热直线W₂在a点相交。这表明，在a点发热功率W₁等于散热功率W₂，介质处于热平衡情况，这时试样的温度为T_a，电压可持续作用，温度不再升高；②若外加电压V₃较高，这时发热功率W₁恒大于散热功率W₂，曲线W₁（V₃）与直线W₂不可能相交，这表明介质在任何温度下都不会达到热平衡，这就使介质温度不断地升高，最后导致热击穿；③在一定电压V₂下，曲线W₁（V₂）与直线W₂相切于c点，相应于c点介质的温度为T_m，这就是介质达到临界热击穿时的最高极限温度。因为T<T_m时，W₁（V₂）>W₂，温度继续上升至T_m，在T_m维持热平衡，电压可持续作用，温度不再升高。而当T>T_m时，W₁（V₂）>W₂，温度继续上升最后导致热击穿。发热曲线W₁（V₂）是介质热稳定与不稳定状态的临界曲线，电压V₂就是固体电介质热击穿电压。由于热击穿电压不仅取决于固体电介质的本质，同时还取决于一系列外界因素，因此热击穿电压往往不作为表征介质特征的参数。

显然，当发热曲线W₁与散热直线W₂相切时，切点c应满足以下条件

这就是固体电介质的热击穿判据。

对于介质损耗较高的固体介质材料，在高频下的主要击穿形式是热击穿。