电介质弛豫与频率响应分析

前面介绍电介质极化微观机制时，曾分别指出不同极化方式建立并达到平衡时所需的时间。事实上只有位移极化可以认为是瞬时立即完成的（严格地讲电子位移极化是瞬时的），其他极化都需要时间，这样在交流电场作用下，电介质的极化就存在频率响应问题。

在一个实际介质的样品上突然加上一电场（阶跃电场），所产生的极化过程不是瞬时的，如图6-12所示。P₀代表瞬时建立的极化（位移极化），P_l代表松弛极化，P₁是时间的函数（可写为P₁（t）），它渐渐达到一稳定值P₁∞。这一滞后通常是由转向极化和空间电荷极化所致。在外电场施加和移去后，系统逐渐达到平衡状态的过程叫介质弛豫。由图6-12可以看出，t时间极化强度P（t）包括两项为

P（t）=P₀+P₁（t） （6-67）

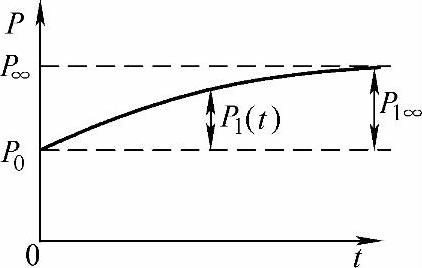
图6-12 介质的弛豫过程

当时间足够长时，P₁（t）→P_1∞，而P（t）→P_∞。设P₀=ε₀χ₀E，P_1∞=ε₀χ₁E（E为宏观电场强度，χ₀为介质的瞬时极化系数，χ1为介质稳态极化系数）。根据弛豫过程的特征方程，有

式中，τ为弛豫时间常数。当t=0时，对于阶跃电场，有P₁（0）=0，因而可得

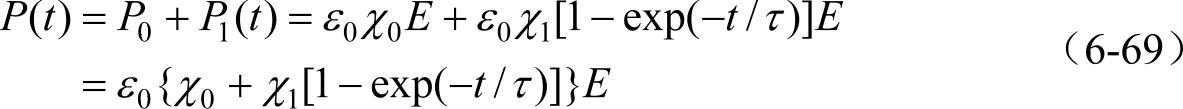
当外加电场是交变电场E=E₀e^icot时，P₁（t）与E具有相同的变化频率（但相位角不一定相同），可设P₁（t）为

式中的A不一定为实数，P₁（t）与E的相位差可包括在A中。将式（6-70）代入式（6-68），并考虑到P_1∞=ε₀χ₁E，可得A为

则

所以

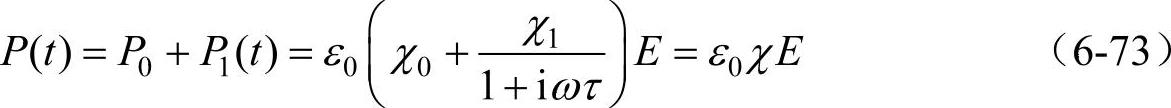(www.xing528.com)

式中，χ为介质的复极化系数。

则介质的复相对介电常数ε_r为

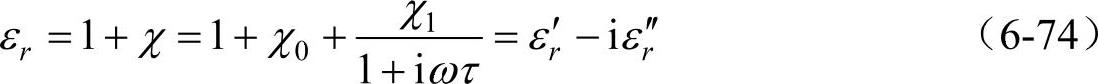
式中，ε_r′和ε_r″分别为复相对介电常数的实部和虚部。那么有

低频或静态时，ε_r′=ε_r0（ε_r0代表静态相对介电常数）；频率ω→∞时，ε_r′=ε_r∞（ε_r∞代表光频相对介电常数），所以有

由式（6-74）、式（6-75）、式（6-76），连同tanδ=ε_r′/ε_r″，可得

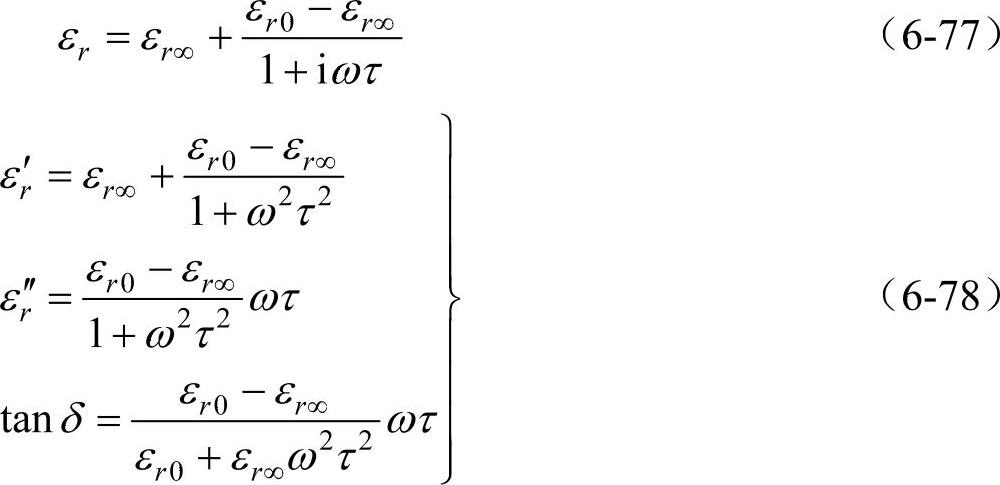
式（6-78）即为德拜公式。

式（6-78）可以分析描述电介质极化和频率、弛豫时间的关系。电介质的相对介电常数（实部和虚部）随所加电场的频率而变化。在低频时，相对介电常数大小与频率基本无关；当ωτ=1时，ε_r″有极大值；当ωτ=（ε_r0/ε_r∞）^1/2时，tanδ有极大值。某种介质根据其ε_r0、ε_r∞、τ值由式（6-78）作图，得到图6-13所示的三条曲线。

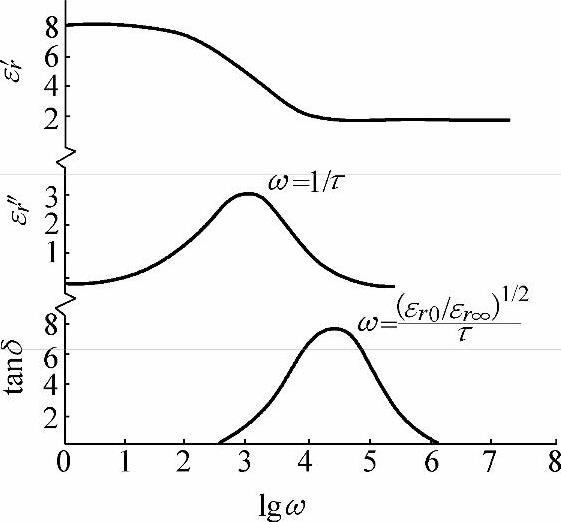
图6-13 ε_r′、ε_r″、tanδ分别与ω的关系曲线

由于不同极化机制的弛豫时间不同，因此，在交变电场频率极高时，弛豫时间长的极化机制来不及响应所受电场的变化，故对总的极化强度没有贡献。图6-14为某一电介质的相对介电常数ε_r（实部）、介电损耗tanδ与频率f的关系。在图6_-14b中，在偶极子松弛极化阶段、离子位移极化阶段（红外光谱范围）、电子位移极化阶段（紫外光谱范围）都有吸收峰。

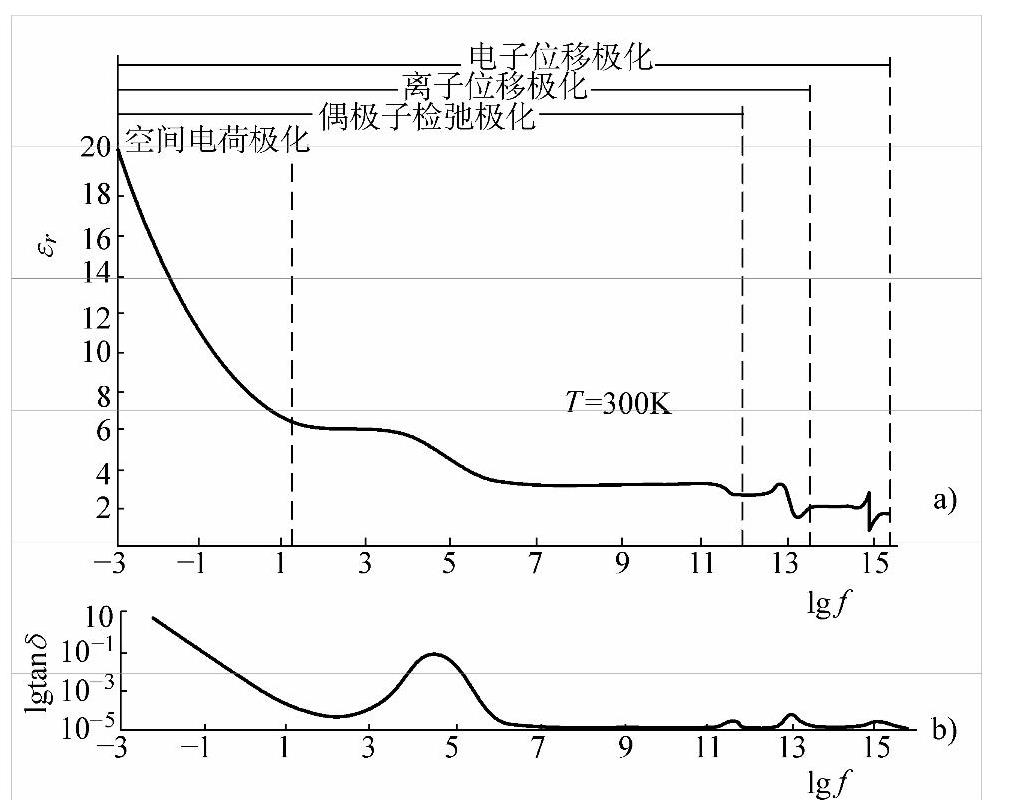
图6-14 相对介电常数ε_r（实部）与频率f关系曲线和介电损耗tanδ与频率f关系曲线