电介质极化机制简析

电介质在外加电场作用下产生宏观的电极化强度，实际上是电介质微观上各种极化机制贡献的结果，它包括电子的极化、离子的极化（两者均又可分为位移极化和松弛极化）、电偶极子取向极化和空间电荷极化等。位移极化是一种弹性的、瞬时完成的极化，不消耗能量。松弛极化与热运动有关，完成这种极化需要一定的时间，并且是非弹性的，因而消耗一定的能量。

1.电子、离子位移极化

（1）电子位移极化

在外电场作用下，原子外围的电子云相对于原子核发生位移，原子中的正、负电荷重心产生相对位移，这种极化称为电子位移极化。电子位移极化的性质具有一个弹性束缚电荷在强迫振动中所表现出来的特性。因为电子很轻，它们对电场的反应很快，可以光频跟随外电场变化。根据玻尔原子模型的经典理论可以计算出电子的平均极化率α_e。

一个点电荷（电子）-e环绕以点电荷（原子核）+q为圆心的圆周轨道运行。垂直于轨道平面的电场E_loc使-e的轨道中心沿轴线从轨道中心M移至点O，移动距离为d，如图6-4所示。则原子感生偶极矩为μ=ed。由图6-4可见，d/R=eE_loc/F_R，F_R为沿轨道运行电子的离心力。由于R》d，则F_R≈e²/（4πε₀R²），因此有

则

电子的极化率α_e为

可见，电子极化率的大小与原子（离子）的半径有关。

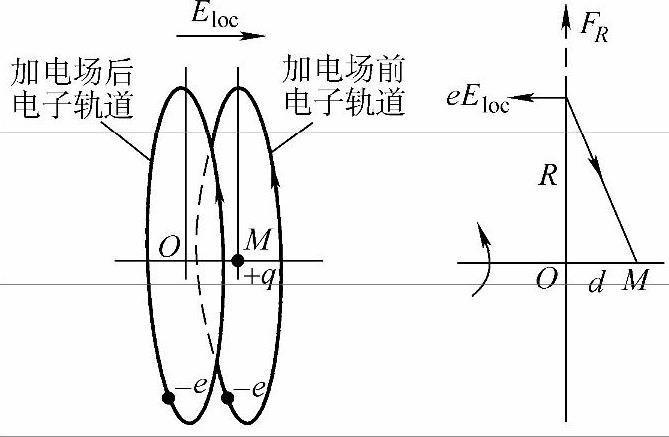
图6-4 轨道模型

若考虑同类原子的一个集合，它们所有轨道是随机取向，则在电场方向上平均感生偶极矩为<μ>=μ<cos²θ>，尖括号表示对其中的物理量求平均值，θ为偶极矩与电场方向的夹角。如电场强度较低，则<cos²θ>=1/3，所以

则

对O-、F-、Na+、Mg2+、S-、Cl-、K+和Ca2+离子半径的X射线测量值与经典理论计算值比较表明，除Mg2+、Ca2+离子外，相符较好，这说明经典模型是有效的。

还可以从另外一个角度估算电子的极化率α_e的大小，如导出电子的极化率α_e和电子与离子组成的弹性偶极子的固有频率的关系。设电子质量为m，电子轨道中心在垂直于轨道平面的交变电场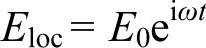（这里E₀为交变电场的幅值，ω为电场交变频率，t为时间）作用下位移为x。电子轨道中心与原子核（离子）的弹性恢复系数为β。则电子的运动方程为

这个振动方程的解为

由式（6-31）得电偶极矩为

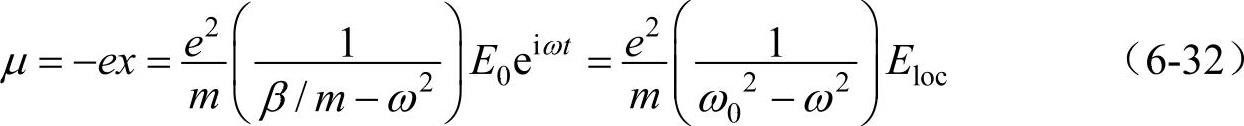
式中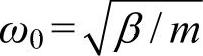，，即为电子与离子组成的弹性偶极子的固有频率。由式（6-32）可得电子的极化率α_e为

令ω→0，得静态极化率α_e0为

由式（6-34）可以看出电子极化率依赖于频率。式（6-33）中极化率与频率的关系反映了极化的惯性。测量电子极化一般在光频（紫光）下进行，此时，其他极化机构（分子、离子极化）由于惯性跟不上电场的变化，因而此时的介电常数ε∞（∞表示交变电场频率很大）几乎完全来自电子极化率的贡献。

（2）离子位移极化

在离子晶体和玻璃等无机电介质中，正、负离子处于平衡状态，其偶极矩的矢量和为零。但这些离子，在电场作用下，除了离子内部产生电子位移极化外，离子本身将发生可逆的弹性位移。正离子沿电场方向移动，负离子沿反电场方向移动，正、负离子发生相对位移，形成感应偶极矩，这就是离子位移极化。离子的相对位移包括离子之间的间距变化和键与键之间夹角的变化。

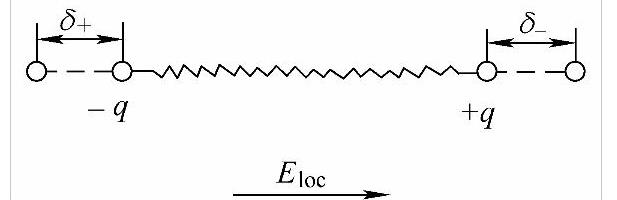
图6-5 离子位移极化模型

为简单起见，取由两个异性离子（正负离子的质量分别为M+和M-，所带电量绝对值均为q）组成的分子来研究离子位移极化率α_i。在平行于正、负离子连线方向上施加电场E_loc=E₀e^icotωt，与电子位移极化类似，在电场中离子的位移，仍然受到弹性恢复力的限制（弹性恢复系数为β）。设正离子位移δ+，负离子位移δ-（δ+与外电场方向相同为正，δ-与外电场方向相反为负），如图6-5所示。则感生的电偶极矩μ_i为

μ_i=q（δ+-δ-）=α_iE_loc （6-35）

在交变电场作用下，两离子的运动方程可写为

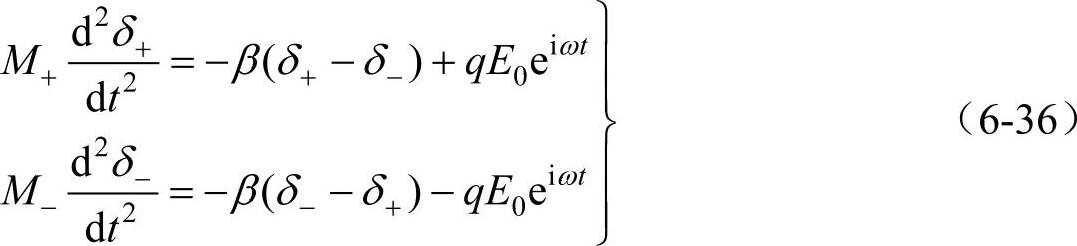
引入相对运动约化质量M*为

则由式（6-36）得

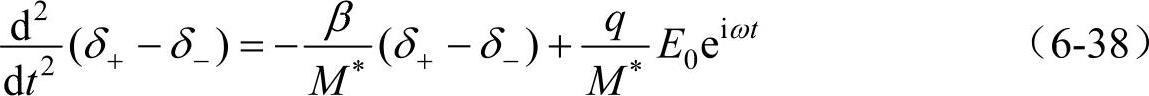
设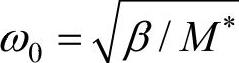为相对振动的固有频率，则式（6-38）的解为

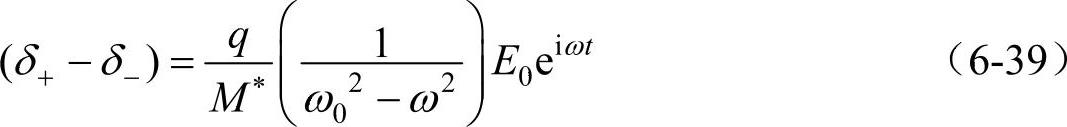
则离子极化率α_i为

令ω→0，得静态极化率

可见，离子位移极化和电子位移极化的表达式一样，都具有弹性偶极子的极化性质。ω₀可由晶格振动红外吸收频率测量出来，从而得到离子位移极化建立的时间约为10^-12～10^-13s。

2.电子、离子和极性分子松弛极化

这种极化机制也是由外加电场造成的，但与带电质点的热运动状态密切相关。例如，当材料中存在着弱联系的电子、离子和偶极子等弛豫质点时，温度造成的热运动使这些质点分布混乱，而电场使它们有序分布，平衡时建立了极化状态。这种极化具有统计性质，称为热松弛（弛豫）极化。极化造成带电质点的运动距离可与分子大小相比拟，甚至更大。

由于是一种弛豫过程，建立平衡极化时间约为10^-2～10^-9s，并且由于创建平衡要克服一定的位垒，故吸收一定能量，因此，与位移极化不同，松弛极化是一种非可逆过程。

松弛极化包括电子松弛极化、离子松弛极化、偶极子松弛极化。多发生在聚合物分子、晶体缺陷区或玻璃体内。

（1）电子松弛极化

由于晶格的热振动、晶格缺陷、杂质引入、化学成分局部改变等因素，使电子能态发生改变，出现位于禁带中的局部能级形成所谓弱束缚电子。例如色心点缺陷之一的“F—心”就是由一个负离子空位俘获了一个电子所形成的。“F—心”的弱束缚电子为周围结点上的阳离子所共有，在晶格热振动下，可以吸收一定能量由较低的局部能级跃迁到较高的能级而处于激发态，连续地由一个阳离子结点转移到另一个阳离子结点，类似于弱联系离子的迁移。外加电场使弱束缚电子的运动具有方向性，这就形成了极化状态，称之为电子松弛极化。

电子松弛极化与电子位移极化不同，是一种不可逆过程。由于这些电子处于弱束缚状态，因此，吸收一定的能量，电子可作短距离运动，运动距离比位移极化的电子大得多，所以极化作用也强烈得多。

但弱束缚电子和自由电子不同，不能远程迁移。因此电子松弛极化和电导不同，只有当弱束缚电子获得更高的能量时，受激发跃迁到导带成为自由电子，才形成电导。由此可见，具有电子松弛极化的介质往往具有电子电导特性。

电子松弛极化主要是折射率大、结构紧密、内电场大和电子电导大的电介质的特性。一般以TiO₂为基础的电容器陶瓷很容易出现弱束缚电子，形成电子松弛极化。含有Nb⁺⁵、Ca⁺²、Ba⁺²杂质的钛质瓷和以铌、铋氧化物为基础的陶瓷，也具有电子松弛极化。

电子松弛极化建立的时间约为10^-2～10^-9s，在电场频率高于10⁹Hz时，这种极化就不存在了。

（2）离子松弛极化

和晶体中存在弱束缚电子类似，在晶体中也存在弱联系离子。在完整离子晶体中离子处于正常结点，能量最低最稳定，称之为强联系离子。它们在极化状态时，只能产生弹性位移，离子仍处于平衡位置附近。而在玻璃态物质、结构松散的离子晶体或晶体中的杂质或缺陷区域，离子自身能量较高，易于活化迁移，这些离子称弱联系离子。弱联系离子极化时，可以从一平衡位置移动到另一平衡位置。但当外电场去掉后离子不能回到原来的平衡位置，这种迁移是不可逆的，迁移的距离可达到晶格常数数量级，比离子位移极化时产生的弹性位移要大得多。然而需要注意的是弱离子弛豫极化不同于离子电导，因为后者迁移距离属远程运动，而前者运动距离是有限的，它只能在结构松散或缺陷区附近运动，越过势垒到新的平衡位置。其越过势垒U_松要比电导势垒U_电导小，如图6-6所示。

以离子晶体晶格缺陷为例，求解离子松弛极化率。如图6-7所示，设晶体中存在着正离子M^+的空位（在B处），这种空位相当于一个负电荷。为了保持电中性，晶格中自然会出现电荷的某种补偿机构。例如，在空位周围出现M⁺⁺。这样，M⁺的空位和M⁺⁺就构成电矩。由于M⁺的空位带负电，当施加外电场于晶体后，它将逆外电场正的方向排列，如图6-7所示，在A位置上的离子M⁺易位到原来的空位B处，亦即正离子空位从位置B过渡到位置A。这样，电矩可以基本上转到和外电场平行的方向。在趋于和外场平行的转动中，电矩必须克服势垒。由于热起伏，电矩克服势垒是可能的。由此可见，电矩由一平衡态过渡到另一平衡态之前必须等待若干时间；换言之，由于电矩在两个或两个以上的平衡位置转动而引起的极化是一个弛豫过程。

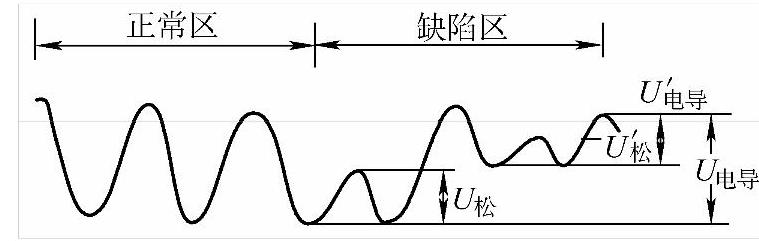
图6-6 离子松弛极化与离子电导势垒(www.xing528.com)

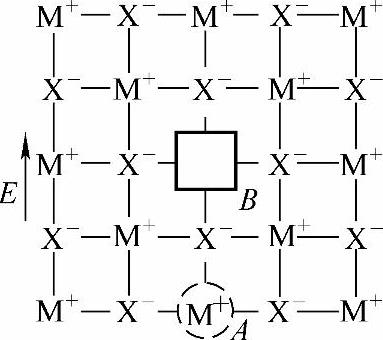
图6-7 空位的移位导致电矩转向

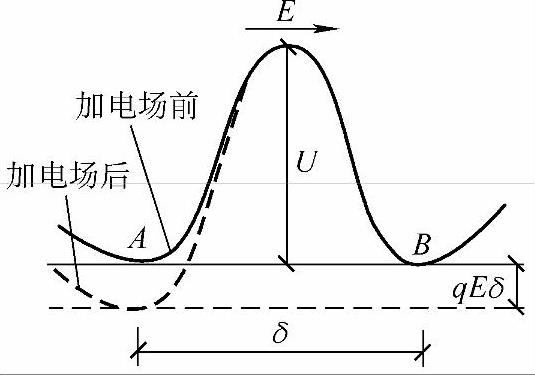
图6-8 施加外电场后势垒变化

设A、B间的势垒为U，如图6-8所示。以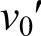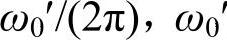（=为角频率）代表离子的振动频率，沿某一方向运动的频率为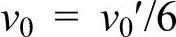。那么，在未加外电场时电矩（即正离子空位）从A向B（或从B向A）过渡的几率P_AB（0）（P_BA（0））为

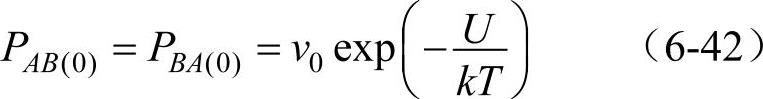
式中，T为绝对温度；k为玻耳兹曼常数。施加外电场E（局部电场）后，A处的势能比B处降低了qEδ（q为离子空位电荷，δ为A、B两点的距离），如图6-8所示。电矩由A向B过渡的几率变为P_AB为

加电场后，由B向A的过渡几率P_BA与未加电场的相同，即P_BA=P_BA（0），因而，电矩处位置A的几率就增加了。如果qEδ《kT，则

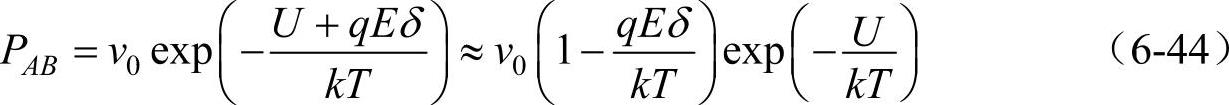
今设单位体积有n_A个正离子空位处于A位，而有n_B个正离子空位处于B位，则

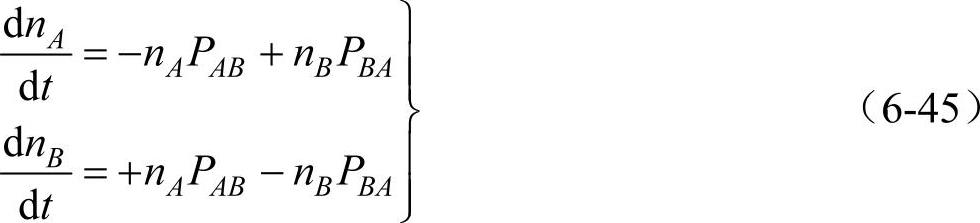
设n为正离子总数，则n=n_A+n_B。由式（6-45）得

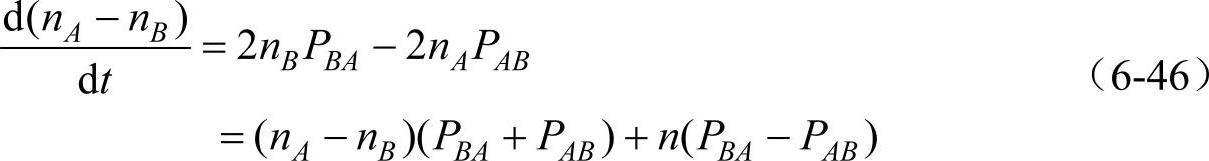
由式（6-42）、式（6-44）及qEδ《kT可得

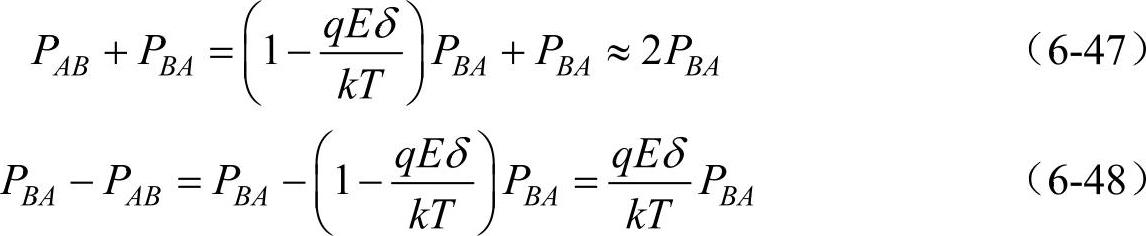
由式（6-47）及式（6-48），式（6-46）变为

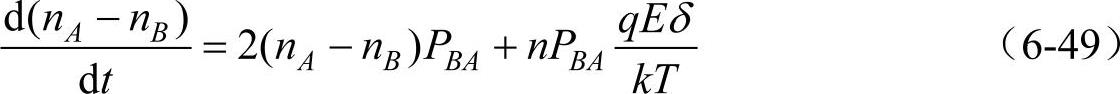
设时间t=0时，n_A=n_B=n/2，且设t=0时加上外电场。在此条件下，式（6-49）的解为

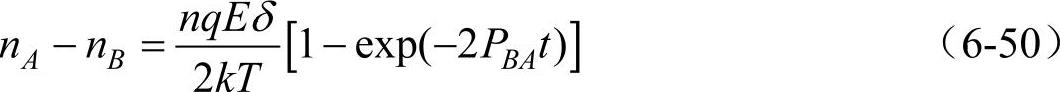
令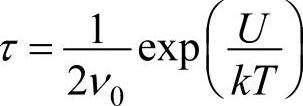（τ为弱联系离子松弛（弛豫）时间常数），那么τ=1/（2P_BA），式（6-50）变为

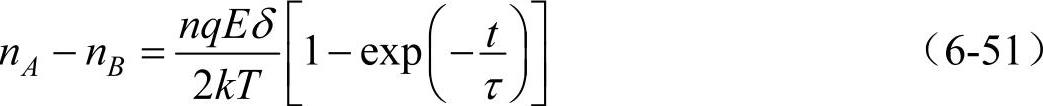
∆n=n_A-n_B实际上为逆电场方向转移的净离子空位数。从式（6-51）可以看出，t→∞时，∆n才稳定。实际上，t=3τ时，极化就基本完成了。极化强度P和热松弛极化率α_T分别为

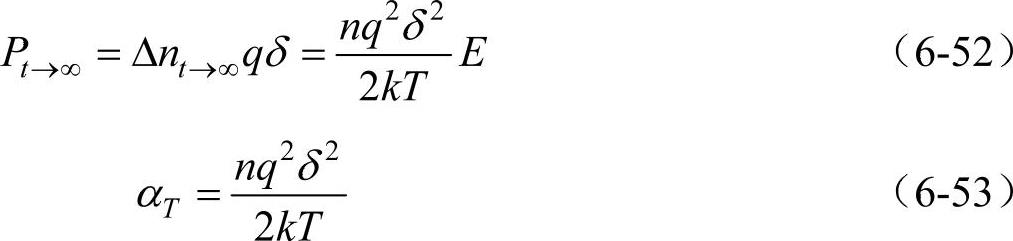
温度越高，热运动对质点的规则运动阻碍越强，因而α_T减小。

由计算可知，离子松弛极化率比电子位移极化率以及离子位移极化率大一个数量级，因而导致较大的介电常数。

在松弛极化P和介电常数ε与温度的关系中往往出现极大值。这是因为，一方面，温度升高，τ减小，松弛过程加快，极化建立得更充分些，这时ε可升高，另一方面，温度升高，极化率α_T下降，使ε降低，所以在适当温度下，ε有极大值。一些具有离子松弛极化的陶瓷材料，其ε—T关系中未出现极大值，这是因为参加松弛极化的离子数随温度升高连续地增加。

离子松弛极化随频率的变化，在无线电频率下比较明显。由于一般松弛时间长达10^-2～10^-5s，所以在无线电频率下（10⁶Hz）离子松弛极化来不及建立，因而介电常数随频率升高明显下降。频率很高时，无松弛极化，只存在电子和离子位移极化（ε趋近于ε∞）。

（3）极性分子固有电矩转向松弛极化

分子具有固有电矩，而在外电场作用下，电矩的转向所产生的电极化称为转向极化。许多电介质，例如一些有极的液体，具有较大的介电常数，这是与其中存在固有电矩有关的。

如果分子具有固有电矩，则在外电场作用下，除贡献电子极化和离子极化外，它们的固有电矩将趋于转到与外电场平行的方向，使介质的极化强度增大，如图6-9所示。特别重要的是，由于固有电矩间的相互作用具有长程有序的性质，一个分子的转向会带来周围许多分子的转向，这样会使得介电常数具有较大的数值。

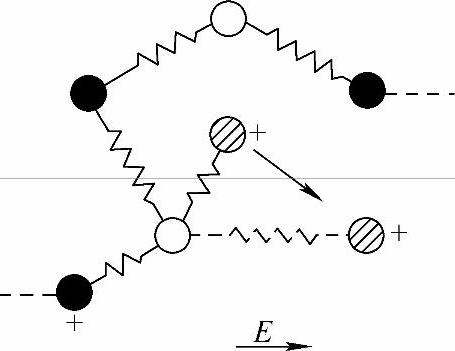
图6-9 极性分子的转向极化

分子中固有电矩的存在，是由于分子结构的不对称性。例如水和氯化氢都有固有电矩。前者是由于H₂O分子并非直线结构（两个OH键夹角为105°），后者则由于电荷在原子周围分布的不均衡，在氢的一端具有较多的正电荷所致。又如CH₃CH₂Br中，由于溴取代氢原子的结果，使得原来对称的分子CH₃CH₃变为不对称，因而也具有固有电矩。

下面来考虑固有电矩在外电场作用下的转向，从而求出其极化率α。在这里的初步考虑中，将忽略固有电矩的相互作用（实际上一个分子的转向会带来周围许多分子转向），这只适用于稀疏情况下的气体。设气体包含大量相同的分子，而每个分子的固有电矩为μ，在没有外电场作用时，由于热运动，这些电偶极子的排列是完全无规则的，因而就整个气体来看，并不具有电矩。当加上外电场E（局部电场）后，每个电矩都受到电场的作用，趋于有序化。另一方面，热运动使电矩无序化。可见同时存在有序化和无序化相矛盾的两个方面。在一定的温度T和一定的电场E下，两方面的作用达到暂时的互相平衡。

固有电矩μ在外电场E的热能为

式中，θ为µ与E间的夹角。根据玻耳兹曼统计，µ与E间的夹角介于θ和（θ+dθ）之间的几率正比于2πδθdθexp[μEcosθ/（kT）]，因此，沿电场方向的平均电矩为

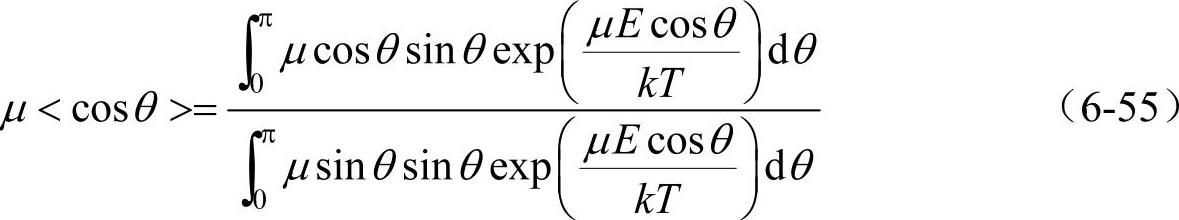
对很大电场E，存在μE》kT，有<cosθ>≈1，这时电场有序化运动超过热无序化，使得所有的电矩都完全平行于电场方向，因此μ<cosθ>=μ。

在E不太大，T不太小时，热运动的无序化作用占相当优势的情况下，可以认为μE《kT，有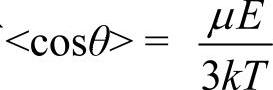。最终可得固有电矩的转向极化率。

转向极化一般需要较长时间，约为10^-2～10^-10s。对于一个典型的偶极子，μ=

-10e×10C·m，因此α≈2×l0^-38F·m²，比电子极化率（l0^-40F·m²）高。

分子的总极化率可以认为是电子极化率、离子极化率和转向极化率的总和。对于单位体积分子数为n的体系，存在关系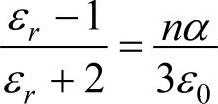。各种极化机制随外电场变化的速度不同，频率较低时，三种极化机制均起作用，随外电场频率增大，固有电偶极矩的取向迟缓而不能跟上电场的变化，频率再高，离子的位移也不能跟上电场的变化，此时电子位移极化起主要作用。

3.空间电荷极化

空间电荷极化常常发生在不均匀介质中。在电场作用下，不均匀介质内部的正负间隙离子分别向负、正极移动，引起介质内各点离子密度变化，即出现电偶极矩。这种极化叫做空间电荷极化。在电极附近积聚的离子电荷就是空间电荷。

实际上晶界、相界、晶格畸变、杂质等缺陷区都可成为自由电荷（间隙离子、空位、引入的电子等）运动的障碍。在这些障碍处，自由电荷积聚，形成空间电荷极化。宏观不均匀性，例如夹层、气泡，也可形成空间电荷极化。所以上述极化又称界面极化。由于空间电荷的积聚，可形成很高的与外电场方向相反的电场，因此这种极化有时称为高压式极化。

空间电荷极化随温度升高而下降。因为温度升高，离子运动加剧，离子扩散容易，因而空间电荷减小。

空间电荷的建立需要较长的时间，大约几秒到数十分钟，甚至数十小时，因而空间电荷极化只对直流和低频下的介电性质有影响。

4.自发极化和高介晶体极化

以上介绍的各种极化机构是介质在外电场作用下引起的，没有外加电场时，这些介质的极化强度等于零。还有一种极化叫自发极化，这是一种特殊的极化形式。这种极化状态并非由外电场引起，而是由晶体的内部结构造成的。在这类晶体中，每一个晶胞里存在有固有电矩。这类晶体称为极性晶体。自发极化现象通常发生在一些特殊结构的晶体中。其机理将在铁电体部分讨论。

由实验得知，大部分离子晶体，例如碱卤晶体、碱土金属的氧化物和硫化物的相对介电常数ε∞约为1.6～3.5，ε_r约为5～12。但是有少数晶体，如金红石（TiO₂）和钙钛矿（CaTiO₃）型晶体，其相对介电常数ε∞和ε_r都相当高，金红石多晶体的ε∞=7.8，εr=110～114；钙钛矿晶体的ε∞=5.3，ε_r=150。这类晶体的介电常数与温度的关系不大，即没有松弛极化的特性。为了说明这这类晶体介电常数大的原因，人们提出一个假设：这类晶体的晶体结构比较特殊，在外电场作用下，由于离子间的相互作用，引起了及其强烈的局部内电场。在此内电场的作用下，离子的电子壳层发生了强烈的变形，离子本身也发生了强烈的位移，这使材料具有很高的介电常数。

计算这类晶体的介电常数时，图6-2中球内原点附近偶极子的影响E₂不但不为零，而且有很大的数值。计算E₂时，可用式（6-16），但通常晶体中存在着好几种性质和相互位置不同的离子。为了研究方便，应把它们所建立的附加内电场区分开。Сκaнaвц导出了金红石晶体的ε_r为

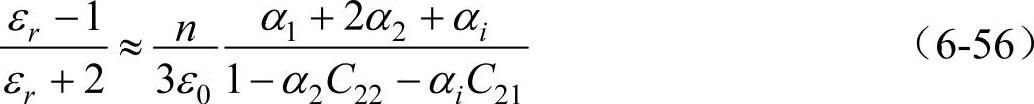
式中，n为单位体积内TiO₂“分子”的个数，即Ti^4+的个数；α₁、α₂分别为Ti⁴⁺、O^2-的电子极化率；α_i为TiO₂“分子”在点阵中的离子位移极化率；C₂₂、C₂₁为晶体的内电场结构系数。当离子位移极化率不存在时，即α_i=0，则得到纯电子极化时的公式

比较式（6-56）和式（6-57）可见，只要加入不大的离子极化率α_i，ε_r比起ε∞来就剧增。Сκaнaвц根据式（6-56）计算的结果与实验结果很接近。

各种极化形式的综合比较如表6-1及图6-10所示。

表6-1 各种极化形式的比较

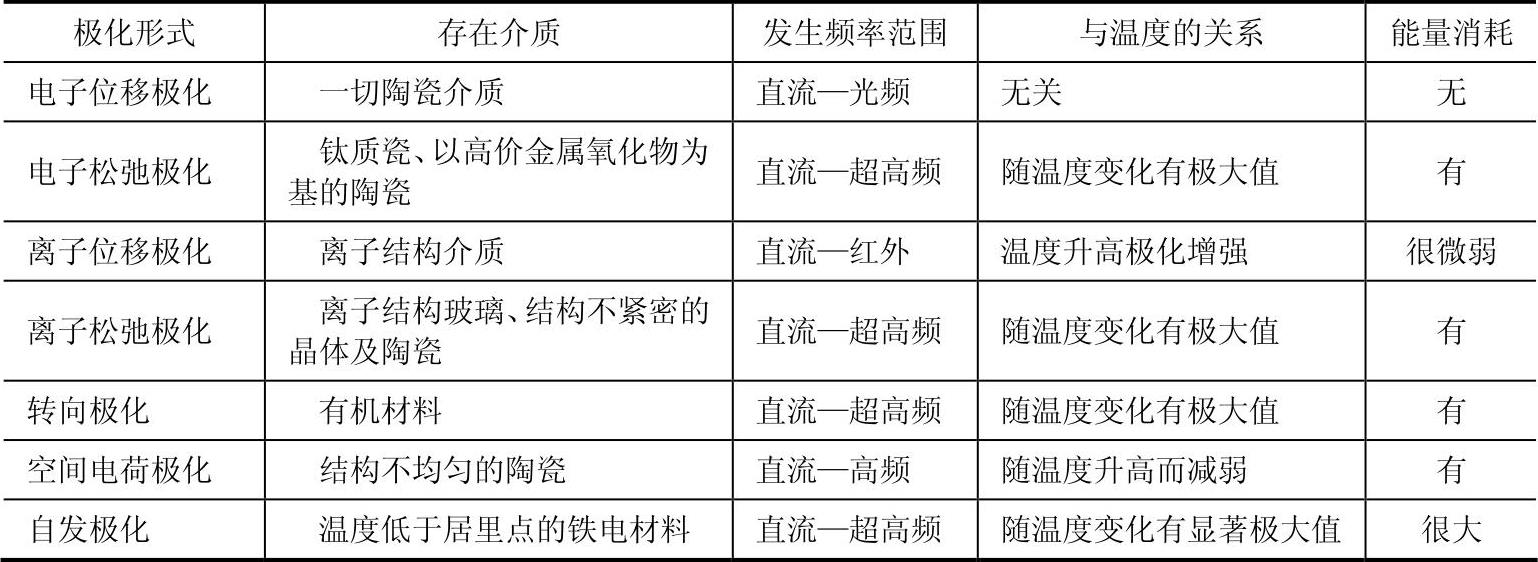
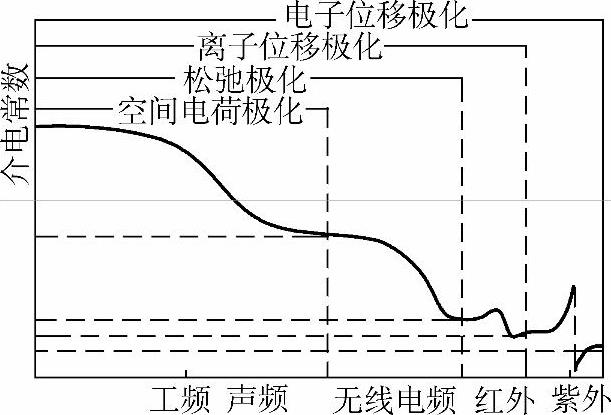
图6-10 各种频率范围对介电常数的影响