静电场中宏观和微观极化的关系探析

1.宏观电场E

上面提到介质宏观平均电场强度的概念，对于介质内宏观电场的的贡献，一是外加电场（由物体外部固定的电荷在真空中所产生的电场）；二是构成物体的所有质点电荷的电场之和。

当介质极化后，它就有了极化强度P，为了求出极化强度P对宏观电场的贡献，可以对样品所有偶极子的和加以简化，如图6-1所示。极化强度P造成的电场可认为是由表面束缚电荷引起的。根据静电学原理，由均匀极化所产生的电场等于分布在物体表面上的束缚电荷在真空中产生的电场。令此电场强度为E_d，它和外加电场E₀方向相反，因而称之为退极化场，如图6-1所示。一个椭球形样品在外电场下能产生均匀的极化强度和均匀的退极化场。这样对宏观场的贡献完全来自外加电场E₀和退极化场强度E_d（矢量和），即

E=E₀+E_d （6-10）

图6-1 退极化场Ed

2.质点位置上的局部电场E_loc

作用在一个质点位置上的局部电场（有时称为有效电场），其数值与宏观电场之间相差甚大。介质中作用于一个质点位置上的局部电场是外加电场E₀及介质中其他质点所产生的电场之和。对其他质点的偶极子场求和的标准方法是以一个想象的参考质点为球心划出一个球，如图6-2所示。该圆球半径应比质点间距大得多，这样对讨论的球心质点来说，球外电介质可作为连续介质，即为均匀介质。同时，球半径又比整个介质（椭球样品）小得多，因此对宏观来说，可视球内为均匀的，即宏观电场对球内各点作用一样。一般可选球半径为质点间距的几十到几百倍。洛伦兹（H.A.Lorentz）设想把球挖空，使球外介质的作用归结为空球表面极化电荷作用场（E₁）和整个介质外边界表面极化电荷作用场（E_d）之和，球内则只考虑原点附近偶极子的影响即E₂，如图6-2所示。所以对一个参考质点（球心）来说，局部电场为

式中，E₁称为洛伦兹场。

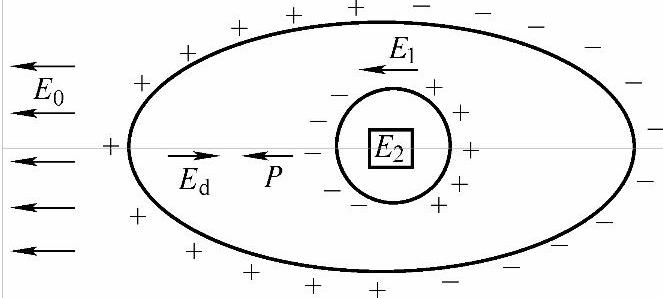
图6-2 介质中质点上的内电场

洛伦兹曾计算此设想的空腔表面上的极化电荷所产生的电场E₁。如图6-3所示，以θ表示相对于极化方向的夹角，θ处空腔表面上的面电荷密度就是-Pcosθ（P为极化强度），取dθ角对应的微小环球面，其表面积为dS。dS面上的电荷dq为

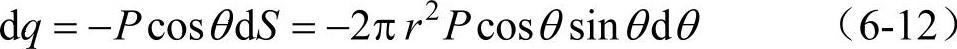
dq在空腔球心0点产生的电场（在P方向上的投影）为

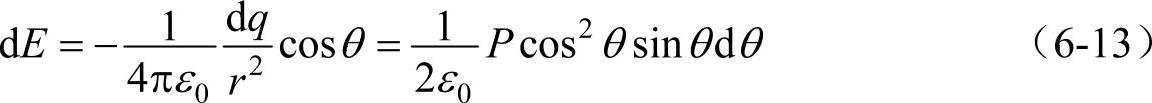
则整个空腔球面上的电荷在球心产生的电场（洛伦兹场）为

图6-3 球形空腔 电场计算

现在来讨论球内其他质点所产生的电场E₂。令球内其他质点（分子、原子、离子）j的坐标为x_j、y_j、z_j；而质点电矩μ_j的三分量为μ_jx、μ_jy、μ_jz；则这些电矩在中心处所产生的电场沿外场方向（设为x向）的分量亦即所需求的E₂，为

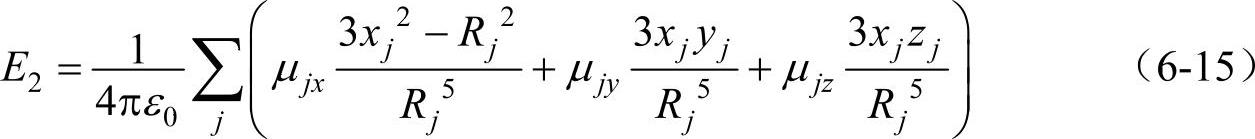
式中，

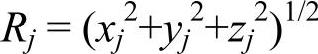
，为电矩_μj的位矢长度。对于由同种原子（或离子）组成的简立方晶体。设立方体的一边同宏观电场E的方向重合（在x向），则μ_jy=μ_jz=0，令a为晶格常数，原子j的坐标为（al_j1，al_j2，al_j3），则(www.xing528.com)

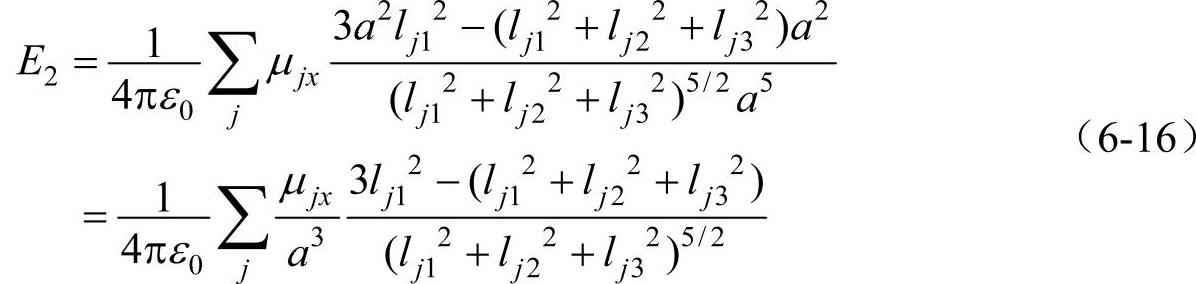
由于简单立方晶体的对称性，在球壳内，有

故式（6-16）等于零，即

E₂=0 （6-18）

同样，对于体心立方、面心立方，以及氯化钠结构的晶体，也可以证明E₂=0，对于具有这类结构的晶体，有效场

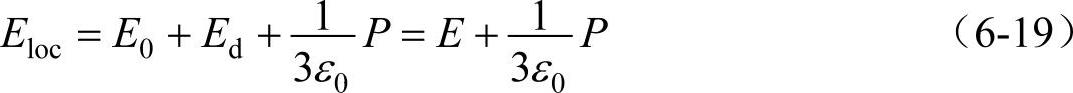
式中，E为宏观电场。这就是洛伦兹关系。关于立方对称离子晶体的实验数据证明洛伦兹关系是正确的。

决不能认为所有具有立方结构的晶体，它们的E₂都等于零。例如钛酸钡（BaTiO₃）虽属立方结构，但其中氧的周围并不是立方对称的，因而E₂不等于零。所以在应用式（6-19）时必须慎重。事实上，对于具体的问题应该从式（6-15）出发实际计算E₂。对于复式格子，不同原子（或离子）的周围情况不同，作用在不等同的原子（或离子）处的有效场不同，对于E₂应该就不同中心原子或离子进行计算。

另外必须指出的是，上面的考虑近似地适合于电子或离子的位移极化，而对于固有电矩的转向极化，上述的有效场则全然失效，这是因为洛伦兹模型中在考虑球外对球内中心分子电矩的长程作用时，过多地计算了转向的影响。

3.克劳修斯—莫索蒂方程

根据D、E和P的关系可知

P=D-ε₀E=（ε-ε₀）E=ε₀（ε_r-1）E （6-20）

将式（6-20）代入式（6-19）得

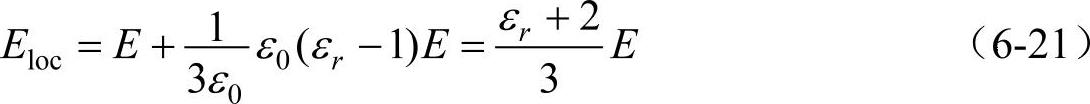
由式（6-5）、式（6-20）和式（6-21）可得

即

此式称为克劳修斯—莫索蒂方程。它建立了宏观量ε_r与微观量α之间的关系。此式适用于分子间作用很弱的气体、非极性液体和非极性固体以及一些型离子晶体和具有适当对称的晶体。

对具有两种以上极化质点的介质，上式可变为

式中，nk、αk分别为介质中的第k种极化质点的单位体积数量和质点的极化率。由式（6-20）可看出，为了获得高介电常数，除了选择α大的离子外，还要求n大，即单位体积的极化质点数要多。