杂质半导体：掺杂与导电的关系

通常制造半导体器件的材料是杂质半导体。在本征半导体中人为地掺入五价元素或三价元素将分别获得n型（电子型）杂质半导体和p型（空穴型）杂质半导体。

1.n型半导体

在本征半导体中掺入五价元素的杂质（磷，砷，锑）就可以使晶体中的自由电子的浓度极大地增加。这是因为五价元素的原子有五个价电子，当它顶替晶格中的一个四价元素的原子时，它的四个价电子与周围的四个硅（或锗）原子以共价键相结合后，还余下了一个价电子变成多余的，成为自由电子，如图5-6a所示。理论计算和实验结果表明，这个价电子能级ε_D非常靠近导带底，ε_C-ε_D比ε_g小得多（ε_C-ε_D的值在锗中掺磷为0.012eV，在硅中掺锑为0.039eV）。所以在常温下，每个掺入的五价元素原子的多余价电子都具有大于ε_C-ε_D的能量，都可以进入导带成为自由电子，因而导带中的自由电子数比本征半导体显著地增多。把这种五价元素称为施主杂质（因其能提供多余价电子），ε_D称为施主能级，ε_C-ε_D称为施主电离能。图5-6b、c示出了n型半导体的能带图。

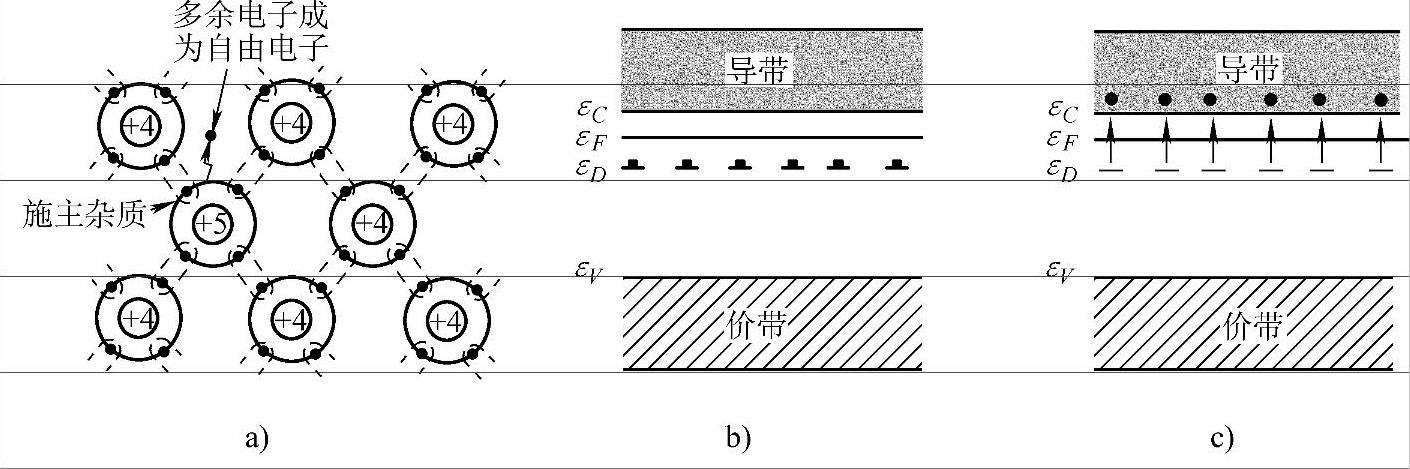
图5-6 n型半导体

a）纯硅掺杂晶格结构示意图 b）0K时施主能级 c）室温时施主能级

在n型半导体中，由于自由电子的浓度大（1.5×10²⁰个/m³），故自由电子称为多数载流子，简称多子。同时由于自由电子的浓度大，由本征激发产生的空穴与它们相遇的机会也增多，故空穴复合掉的数量也增多，所以n型半导体中空穴的浓度（1.5×10¹²个/m³）反而比本征半导体中的空穴浓度小，故把n型半导体中的空穴称为少数载流子，简称少子。在电场作用下，n型半导体中的电流主要由多数载流子自由电子产生，也就是说，它是以电子导电为主，故n型半导体又称为电子半导体，施主杂质也称n型杂质。

2.p型半导体

在本征半导体中，掺入三价元素的杂质（硼，铝，镓，铟），就可以使晶体中空穴浓度大大增加。因为三价元素的原子只有三个价电子，当它顶替晶格中的一个四价元素原子，并与周围的四个硅（或锗）原子组成四个共价键时，必然缺少一个价电子，形成一个空位置，如图5-7a所示。在价电子共有化运动中，相邻的四价元素原子上的价电子就很容易来填补这个空位，从而产生一个空穴。理论计算和实验结果表明，三价元素形成的允许价电子占有的能级ε_A非常靠近价带顶，即ε_A-ε_V远小于ε_g的值（ε_A-ε_V的值在硅中掺镓为0.065eV，掺铟为0.16eV，锗中掺硼或铝为0.01eV）。在常温下，处于价带中的价电子都具有大于ε_A-ε_V的能量，都可以进入ε_A能级。所以每一个三价杂质元素的原子都能接受一个价电子，而在价带中产生一个空穴。我们把这种三价元素称为受主杂质（因其能接受价电子），ε_A称为受主能级，ε_A-ε_V称为受主电离能。图5-7b、c示出了p型半导体的能带图。

图5-7 p型半导体

a）纯硅掺杂晶格结构示意图 b）0K时受主能级 c）室温时受主能级

在p型半导体中，因受主杂质接受价电子产生空穴的作用，使空穴浓度大大提高，故空穴为多数载流子。同时，因空穴多，本征激发的自由电子与空穴复合的机会增多，故p型半导体的自由电子浓度反而比本征半导体中的自由电子少，即电子是少数载流子。在电场的作用下，p型半导体中的电流主要由多数载流子空穴产生，即它是以空穴导电为主，故p型半导体又称空穴型半导体，受主杂质又称p型杂质。

n型半导体和p型半导体统称为杂质半导体，与本征半导体相比，具有如下特性：掺杂浓度与原子浓度相比虽很微小，但是却能使载流子浓度极大地提高，导电能力因而也显著地增强。掺杂浓度愈大，其导电能力也愈强；掺杂只是使一种载流子的浓度增加，因此杂质半导体主要靠多子导电。当掺入五价元素（施主杂质）时，主要靠自由电子导电。当掺入三价元素（受主杂质）时，主要靠空穴导电。

3.杂质半导体电子和空穴数

式（5-27）、式（5-29）分别为计算本征半导体电子和空穴数的公式。在推导时并没有特殊规定，只是在能量上费米能级到导带底部的能量是kT的许多倍。这些同样适用于非本征半导体。问题的复杂性在于如何确定费米能级并且同时考虑施主和受主能级。条件是晶体必然是电中性，净电荷浓度必然是零。在非本征半导体中，杂质原子捐赠一个电子到导带，并留下一个正电荷，最终则有一个受主原子，接受从价带来的电子，那么便有一个负电荷，从而使其电中性公式为

式中，n_e、nh分别为自由电子和空穴的浓度（单位体积的个数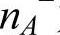）；为游离的受主原子（原子接受一个从价带来的电子）的浓度；n_D^+为游离的施主原子（原子捐赠一个电子到导带）的浓度。

怎样从实际杂质原子浓度n_A和n_D中找到游离杂质的浓度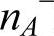和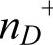+，以图5-6b为例，0K时所有施主能级皆被电子所占有，只要得到ε_g-ε_D的能量，则可成为导电的电子。因此可由这个能量数值来计算出nD+。换句话说，如果以没有占据εD能级的电子的几率乘以nD，便可得到nD+，即

受主的情况类似。电子占据ε_A能级的几率是f（ε_A），则

对某一确定的半导体，即已知n_A和n_D、能隙ε_g以及电子和空穴的有效质量，把式（5-27）、式（5-29）、式（5-35）、式（5-36）表示的ne、nh、nD+、nA-代入式（5_-34），便可以算出ε_F。

对n型半导体，ne》nh，nD+》nA-，则式（5-34）简化为

这说明，所有导电电子来自施主能级，而不是基体的晶格键合，把n_e及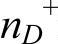表达式代入式（5-37）得

式中，n_C=2（2πm_e*kT/h²）^3/2。计算时可以假设价带顶部的能量为零，则ε_F-ε_C=ε_F-εg，式（5-38）即为(www.xing528.com)

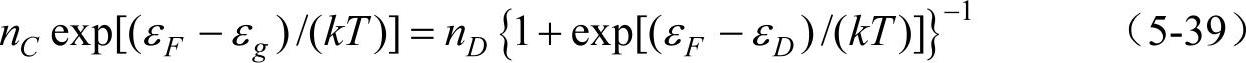
由式（5-39）得到

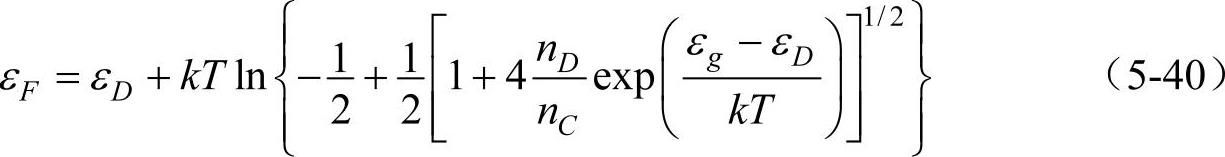
从式（5-40）可见，ε_F是温度的函数。现分三个温度区域讨论式（5-40）的物理意义。

①在低温时，exp[（ε_g-ε_D）/（kT）]》1，则

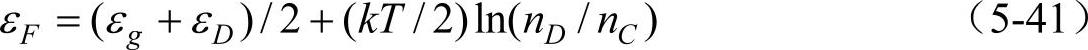
导电电子浓度为

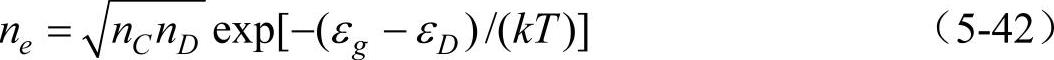
式（5-41）说明费米能级位于导带底和施主能级之间（ln（n_D/n_C）<0）。

②当温度升高至exp[（ε_g-ε_D）/（kT）]≈1时，则

导电电子浓度为

n_e=n_D （5-44）

式（5-43）说明费米能级随温度升高，不断向本征半导体费米能级接近。因为在这个区域施主能级的电子全部跃迁至导带。

③更高的温度区域时，半导体成为本征半导体。此区域即为本征区域。费米能级近似位于禁带中央。

图5-8a表示上述分析结果的物理图像。

对p型半导体也可以做类似的讨论，结果表示在图5-8b中。图5-8c说明杂质含量对非本征半导体费米能级位置的影响。如图5-8c所示，对于n型半导体，当施主浓度为10²⁶m^-3时，费米能级在600℃以下靠近导带的底部。随着施主浓度的减少，费米能级向比导带更低的能量方向移动；对于p型半导体，当受主浓度为10²⁵m^-3时，费米能级在400℃以下位于接近价带的顶部，随着受主浓度减少，费米能级向价带顶部更高能量方向移动。

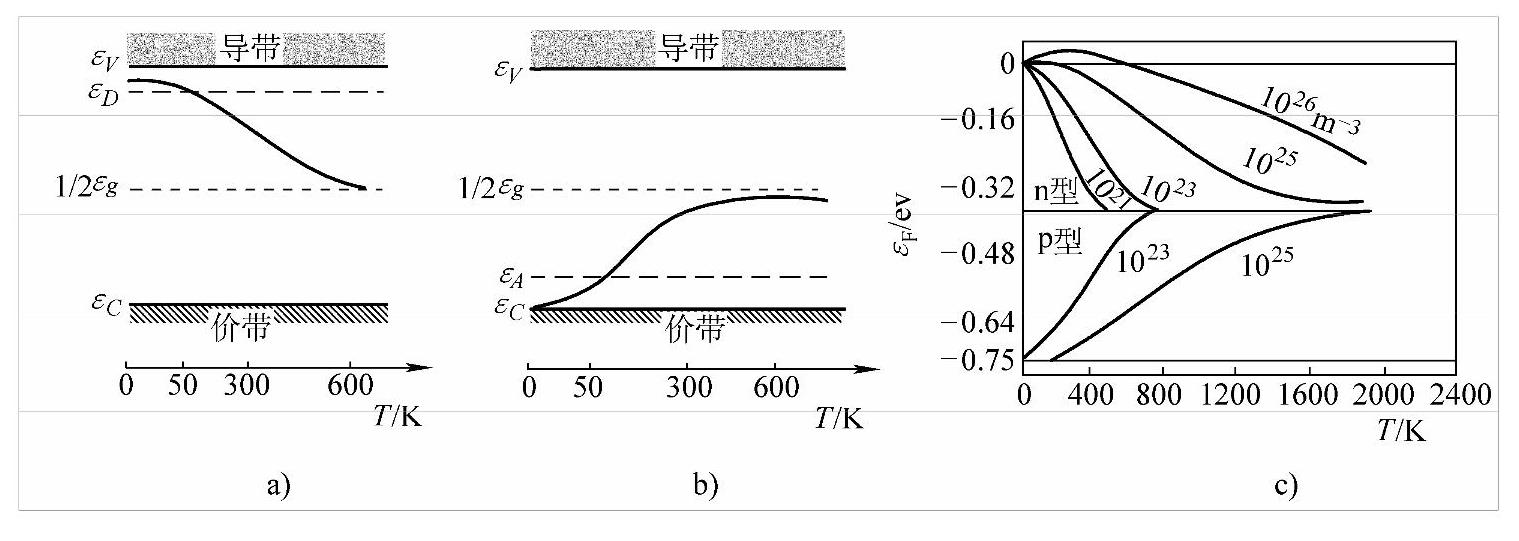
图5-8 费米能随温度的变化

a）n型半导体 b）p型半导体 c）不同掺杂浓度的n型和p型Ge半导体

4.杂质半导体迁移率与温度的关系

图5-9a所示为测得的含不同杂质浓度Ge半导体电阻率ρ与温度T的关系曲线。已知其各温度下的霍耳常数，那么便可绘出Ge的空穴迁移率_μh与温度T的关系，如图5-9b所示。

载流子由于晶格的热振动而被散射，迁移率_μ与温度T具有T^-3/2的关系。离子化的杂质同样散射载流子，杂质含量愈高，迁移率愈低。图5-9b说明在高温或者低杂质浓度时晶格散射起主要作用；当杂质浓度高时，杂质散射起主要作用。

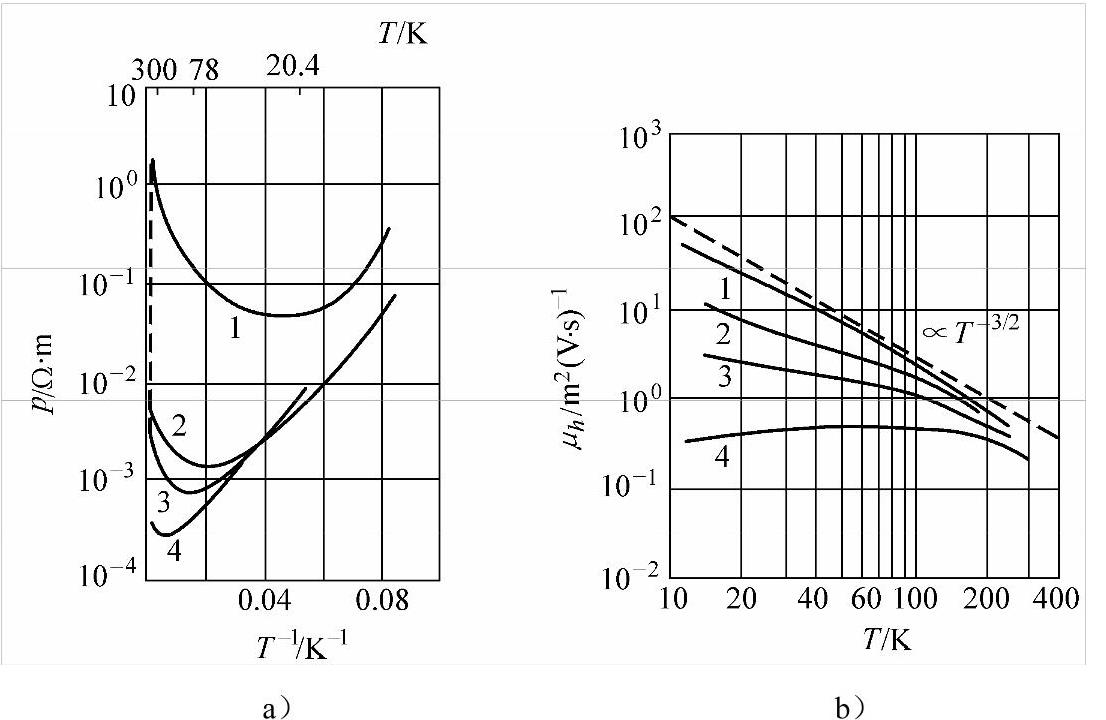
图5-9 Ge电性能与温度的关系

a）电阻率ρ与温度T的关系 b）空穴迁移率μ_h与温度T的关系杂质浓度（n_D-n_A）/m³：1—1.0×10¹⁹2—1.7×10²¹3—7.5×10²¹4—5.5×10²²