固体传热的微观机理及优化探讨

1.声子热导

如果不考虑电子对热传导的贡献，则晶体中的热传导主要依靠声子来完成。在没有温度梯度时，声子在各方向上作无规运动。存在温度梯度时，由声子把能量从一端传递到了另一端，能流密度不为零。声子不是畅通无阻地由一端行进到另一端，在通过样品的扩散过程中遭到频繁的碰撞。通常把声子的前后两次碰撞间走过的平均距离l称为声子的平均自由程。利用上述模型，把经典气体分子运动论中关于热导率的理论移植到声子热传导的问题中来。声子的热导率为

式中，c_V是晶格（声子）质量定容热容；ν是声子平均速度的大小，就是布里渊区中全部占据态（声子）平均速度的大小。

在式（4-78）中，c_V是与温度相关的，平均自由程l由散射过程决定，显然也与温度密切相关，只有ν基本上与温度无关，所以热导率λ是温度的函数。c_V与温度的关系在前面已经给出，要了解热导率λ的温度相关性，现在关键是了解平均自由程l与温度的关系。

平均自由程l与温度T的关系决定于在晶体中发生的碰撞（散射）过程，这个问题是非常复杂的。可简单归纳为如下几个重要的散射机制：声子之间的散射；声子受晶体中点缺陷（杂质、空位等）的散射；声子受样品边界的散射。与每一种散射机制相联系有一个平均自由程l_a、l_b、l_c，因而产生相应的热阻为W_a、W_b、Wc。总热阻为W=W_a+Wb+Wc。总的平均自由程l为

如果上述几种散射强度相当，l与T的关系问题必然十分复杂。这里只讨论简单情况，即某一温度范围内，假设只有一种散射机制起主导作用。

（1）声子与声子的相互作用

如果原子间的力是纯谐和的，则不存在不同声子间的碰撞机制，而平均自由程将只受到声子同晶体边界的碰撞以及点阵缺陷的限制。在有些情况下，这些效应起主导作用。然而，如果存在非谐点阵相互作用，在不同声子间就出现一种耦合，它限制平均自由程的值。非谐系统精确的简正模式不再像纯声子。下面考虑由声子相互作用引起的热阻率。

1）正常过程和倒逆过程 随着温度升高，原子间的位移变大，必须考虑非谐效应。声子不再是互相独立的，它们之间互相散射。散射过程遵守能量守恒和准动量守恒定律。设两个声子的频率和波矢分别为ω₁、q₁和ω₂、q₂，碰撞产生的第三个声子频率和波矢为ω₃、q₃。能量守恒：ћω₁+ћω₂=ћω₃；准动量守恒：ћq₁+ћq₂=ћq₃+ћG，这里G为倒格矢。

如果G=0，q₁、q2、q3都在第一布里渊区，声子碰撞前后系统的动量严格相等，能量不变。这样的过程不产生热阻，它不影响整个声子系统的流动。这种过程叫正常过程，也叫N过程。在N过程中，由散射引起的波矢的改变q₁-q₂-q₃=0，声子集团的动量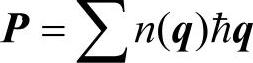守恒，式中n（q）表示波矢为q的声子数。对于P≠0的分布，N过程使P保持不变。即如果沿一根棒状样品推动一个初始P≠0的声子分布集团，则该分布沿这根棒传播而P不变。因此没有热阻，即热导率是无限的。

如果G≠0，这相当于q₁和q₂在第一布里渊区，q₃不在第一布里渊区（超出第一布里渊区的范围），如图4-20所示。有物理意义的波矢都在第一布里渊区内。我们可以把q₃约化到第一布里渊区之内，用q₄代表，q₄=q₃-G。值得注意的是，由声子碰撞产生的有意义的波矢q₄的方向与原来q₁、q₂的方向几乎相反。在碰撞过程中初态和终态动量差非零倒格矢，这种过程对于改变声子动量起很重要的作用，是高温情况下影响平均自由程的决定性因素，这个过程引起热阻。把这种过程称为倒逆过程，也叫U过程。

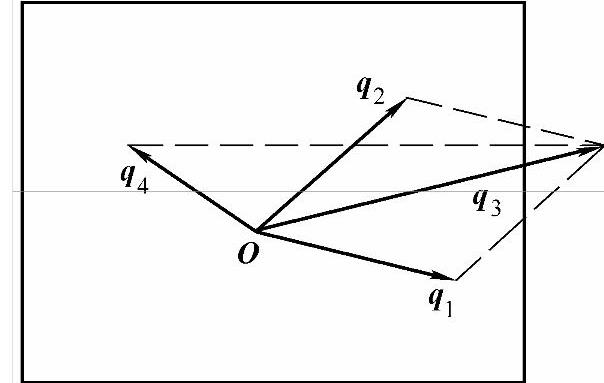
图4-20 倒逆过程

2）倒逆过程对热导的影响 如果两个声子散射后产生第三个声子，只有q₁、q₂波矢大小具有（1/2）G的量级，才可能发生q₁+q₂=q₃+G的倒逆过程，引起热阻。根据德拜理论，这两个参与碰撞的声子的能量为（1/2）kΘ_D量级。

在高温下（T》Θ_D），有

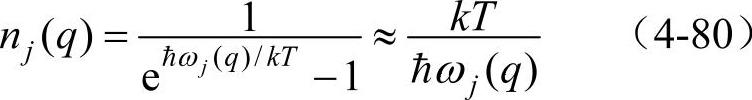
所以总的声子数目是和T成正比的，能够参与倒逆过程的声子数目也与T成正比。由于声子数多少与碰撞几率成正比，因此，1/τ∝T（τ为声子两次碰撞的平均时间间隔），即l∝1/T。由于在高温下质量定容热容c_V遵循杜隆—珀蒂定律，与温度无关，所以此时的热导率随温度升高而降低，即

实际上，更精确的理论分析可以导出λ∝1/T^x，这里x介于1到2之间，这一点已经被实验所证实。

在低温下（T<Θ_D），因为能够产生热阻的倒逆过程的声子能量必须为（1/2）G量级，这样的声子数为

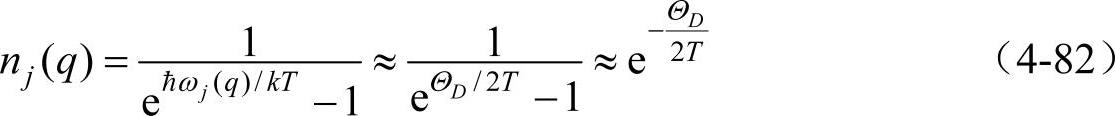
由此可见，温度下降时，能够参与倒逆过程的声子数按指数方式随T急剧减少，没有倒逆过程，热导率应是无限大的。因此可以预见，在T<Θ_D时，热导率公式（4-78）中的有效平均自由程将随e^ΘD/2T改变。这种指数形式，与实验符合得很好。注意：式（4-78）中出现的声子平均自由程是声子之间倒逆过程的平均自由程，而不是声子之间所有碰撞的平均自由程。表4-2中列出几个代表性的平均自由程数值。

表4-2 声子平均自由程（代表性的声速取5×10⁴m/s）

注：石英的测量平行于光轴。

（2）缺陷对声子的散射

在限制平均自由程方面，几何效应也是很重要的，必须考虑由晶体边界、杂质、缺陷等引起的散射。

点缺陷对声子的散射，取决于点缺陷相对于声子波长来说有多大。点缺陷的尺寸越小，散射越小，平均自由程越长。

在低温下，前面描述过的倒逆过程和点缺陷等杂质散射都很小。所以平均自由程将增加，如果平均自由程l可以与样品的宽度相比拟时，则l值将受到这个宽度的限制，它不再是温度的函数。于是声子平均自由程为常值。在式（4-78）中，热导率唯一依赖于温度的因子是质量定容热容c_V，在低温下c_V按T³变化，所以λ∝T³。图4-21给出了低温下氟化锂晶体的热导率λ。从图中可以看出，热导率受到表面散射的限制。在T<10K时，热导率λ∝T³，来自于低温质量定容热容c_V对温度的依赖关系，而且样品尺寸越大，热导率也越大。当温度再升高时，倒逆过程开始起作用。热导率随温度升高而迅速减小，开始以^eΘD/2T形式，之后以1/T形式减少。注意在声子之间散射的平均自由程与样品尺寸相当时，热导率达最大值。

2.光子热导(www.xing528.com)

固体中除了声子的热传导外，还有光子的热传导。这是因为固体中分子、原子和电子的振动、转动等运动状态的改变，会辐射出频率较高的电磁波。这类电磁波覆盖了一较宽的频谱。其中具有较强热效应的是波长在0.4～40μm间的可见光与部分近红外光的区域。这部分辐射线就称为热射线。热射线的传递过程称为热辐射。由于它们都在光频范围内，其传播过程和光在介质（透明材料、气体介质）中传播的现象类似，也有光的散射、衍射、吸收和反射、折射。所以可以把它们的导热过程看做是光子在介质中传播的导热过程。

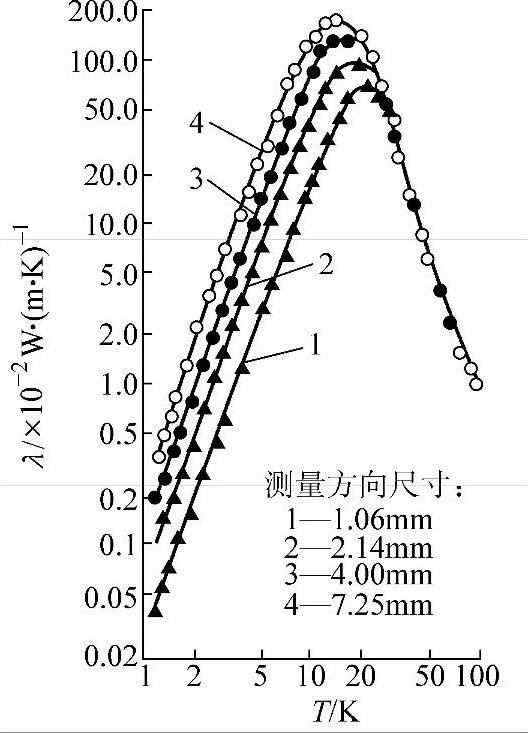
图4-21 氟化锂晶体的热导率

在温度不太高时，固体中电磁辐射能很微弱，但在高温时就明显了。因为其辐射能量与温度的四次方成正比。例如，在温度T时黑体单位容积的辐射能E_T为

式中，σ是斯忒藩—玻耳兹曼常量（为5.67×10^-8W/（m²·K⁴））；n是折射率；c是光速（3×10⁸m/s）。

由于辐射传热中，质量定容热容相当于提高辐射温度所需的能量，所以

同时辐射线在介质中的速度ν_r=c/n，以及将式（4-84）代入式（4-78），可得到辐射能的热导率λr

l_r是辐射线光子的平均自由程。

对于介质中辐射传热过程，可以定性地解释为：任何温度下的物体既能辐射出一定频率的射线，同样也能吸收类似的射线。在热稳定状态，介质中任一体积元平均辐射的能量与平均吸收的能量相等。当介质中存在温度梯度时，相邻体积间温度高的体积元辐射的能量大，吸收的能量小；温度较低的体积元正好相反，吸收的能量大于辐射的，因此，产生能量的转移，整个介质中热量从高温处向低温处传递。λ_r就是描述介质中这种辐射能的传递能力。它极为关键地取决于辐射能传播过程中光子的平均自由程l_r。对于辐射线是透明的介质，热阻很小，l_r较大；对于辐射线不透明的介质，l_r很小；对于完全不透明的介质，l_r=0，在这种介质中，辐射传热可以忽略。一般，单晶和玻璃对于辐射线是比较透明的，因此在773～1273K辐射传热已很明显，而大多数烧结陶瓷材料是半透明或透明度很差的，其l_r要比单晶和玻璃的小得多，因此，一些耐火氧化物在1773K高温下辐射传热才明显。

光子的平均自由程除与介质的透明度有关外，对于频率在可见光和近红外光的光子，其吸收和散射也很重要。例如，吸收系数小的透明材料，当温度为几百摄氏度时，光辐射是主要的；吸收系数大的不透明材料，即使在高温时光子传导也不重要。在无机材料中，主要是光子的散射问题，这使得l_r比玻璃和单晶都小，只是在1500℃以上，光子传导才是主要的，因为高温下的陶瓷呈半透明的亮红色。

3.电子热导

人们在研究纯金属的热导率时，发现一个引人注意的事实，就是金属的电导率愈高，热导率也就愈高。在室温时，金属的热导率和金属的电导率的比值是一常数，不随金属不同而改变。这就是维德曼（Wiedeman）—弗兰兹（Franz）定律。洛伦兹（Lorentz）研究不同的温度T下金属热导率λ和金属的电导率σ的关系时，发现在各温度下λ与σ的比值被相应的绝对温度T除以后，得到的数值对各金属和各温度都是常数。这个常数就叫做洛伦兹常数，以L表示。即

从经典自由电子论可以推导出洛伦兹关系，简略地叙述如下。经典电子论对电导率的表达式为

式中，n₀是单位体积的传导电子数；e是电子的电荷；l是电子的平均自由程；u是传导电子的平均速度；m是电子的质量。

单位体积物质的电子定容热容为c_V^e=（3/2）n₀k，这里k为玻耳兹曼常数。将此式代入式（4-78）得电子的热导率λ_e为

由式（4-87）和式（4-88）得

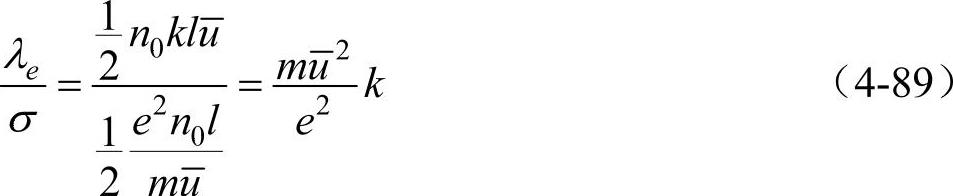
而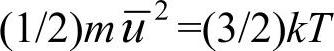，，所以可得

由此可知，当温度一定时，各金属的热导率对电导率之比等于一个相同的常数，而与金属种类无关。在国际单位制中L=2.45×10^-8W·Ω/K²。很多实验工作证明：洛伦兹常数只在较高的温度（>0℃）时才近似为常数，在趋向0K时，洛伦兹常数也趋近于零，这是由于金属中热的传递不仅借助自由电子实现，而且也有赖于离子的振动。另外，对于大多数金属L是符合的，但也不是符合得非常好，不同金属的L有些差别，对于合金差别更大。

如果从总的热导率λ中减去声子热导率λ_t，这样式（4-90）就变为

式中L′是修正后的洛伦兹常数，对所有金属都是常数。修正后的洛伦兹常数对绝大多数金属符合得很好，但只对Be、Cu例外。它对合金也可适用。

即便上述两个规律是近似的，但建立了电导率和热导率之间的联系，也是很有意义的，因为测定热导率较测定电导率要困难，而且结果的准确度也较差。另外，电导率的变化解释起来比热导率较简单。