深度解析因瓦效应的微观机制

人们对因瓦效应的微观机制进行了深入研究，提出了许多的物理模型，但无一种模型占绝对优势。一般认为，因瓦效应与产生磁有序而引起体积效应是密切相关的。因此，目前因瓦理论同铁磁性理论一样分为两大支，即定域电子模型和巡回（巡游）电子模型。

1.定域电子模型

根据定域电子模型，因瓦效应的具体机制主要有以下几种解释。

（1）交换—体积模型

图4-19表示不同金属的贝色—施拉特（Bethe-Slater）交换作用—原子间距曲线（图中r_3d为3d壳层的半径）。由图可见，在正交换作用的上升段（即曲线峰值的左侧），若原子间距为a₁，相应的交换积分为A_l，如交换积分增加到A₂，相应的原子间距增加到a₂。交换积分的增加，使得铁磁体的交换能降低。但另一方面原子间距增加发生弹性变形，提高了弹性能。当交换能与弹性能之和最小时达到平衡。当温度自居里点T_c以上降到T_c以下时发生自发磁化，由于交换积分的增加导致原子间距的改变，且是各向同性的，即发生了体积的变化。这里得到的是正的自发体积磁致伸缩，即ω_s>0（ω_s为自发体积磁致伸缩量）。同样，在正交换作用的下降段（即曲线峰值的右侧），由于磁有序将得到负的自发体积磁致伸缩，即ω_s<0。因瓦合金的ω_s是一个反常大的正值，其数值比一般磁有序物质的高1～2个数量级。因瓦合金在贝色—施拉特曲线峰值左侧，当温度升高时，自发磁化减弱，交换积分A下降，导致原子间距a缩小，从而补偿了晶格振动引起的热膨胀，这就是因瓦合金膨胀系数很小或为负值的原因，也就是因瓦合金负反常热膨胀的物理本质。

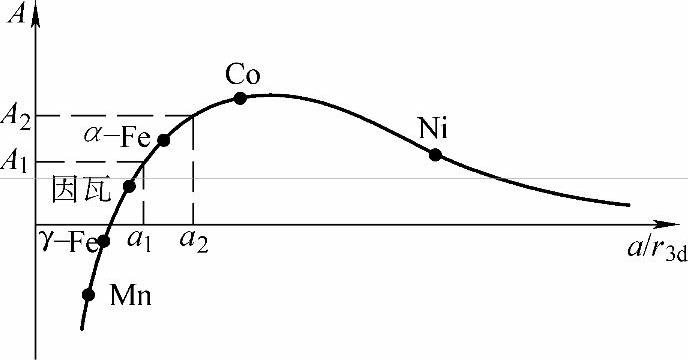
图4-19 贝色—施拉特（Bethe-Slater）曲线

（2）潜存反铁磁性模型

康多尔斯基（Kondorsky）等人认为，在因瓦合金的铁磁基体（体积较大）中有部分的反铁磁性团（体积较小）潜存。温度升高，反铁磁性团增多，导致体积减小。例如Fe-Ni因瓦合金中，Ni-Ni和Fe-Ni原子对呈铁磁性；Fe-Fe原子对呈反铁磁性。

（3）双态模型

外斯（Weiss）假设因瓦合金中存在着γ₁和γ₂两种电子态。γ₁态电子结构为3d^4.0↑3d^3.5↓4s^0.5，是反铁磁态，有较小的体积（晶格常数为0.354nm）和磁矩（原子磁矩为0.5_μB）；γ₂态电子结构为3d^5.0↑3d^2.2↓4s^0.8，为铁磁态，有较大体积（晶格常数为0.364nm）和磁矩（原子磁矩为2.8_μB）。在因瓦成分区域，γ₁和γ₂之间能量差小（约为0.035eV），状态转变对外部条件很敏感。随温度升高，一些γ₂态热激发为γ₁态，由此产生大的自发体积磁致伸缩，因而抵消点阵的热膨胀。

（4）两种交换作用模型

两种交换作用模型，类似潜存反铁磁性模型，不过认为铁磁性来自s电子与d电子的s-d间接交换作用，反铁磁性来自d电子与d电子的d-d直接交换作用。温度升高时，磁矩降低，反铁磁态增加，产生抵消点阵热膨胀的热收缩效应。(www.xing528.com)

（5）施罗斯（Schlosser）模型

施罗斯认为从组织结构上看合金是一种不均匀固溶体。合金由三个区域构成：核心部分是FeNi₃型短程有序区；最外层是γ-Fe；中间是过渡区。因瓦反常与过渡区的状态和数量有关。过渡区中的铁原子取决于近邻原子情况而表现出不同的电子状态和体积。过渡层体积愈大，因瓦反常愈显著。

（6）浓度起伏模型

卡奇（Kachi）和阿桑诺（Asano）基于低镍Fe-Ni合金中铁磁相和反铁磁相共存这一事实，提出了浓度起伏模型。指出，在含镍30%～35%（原子的摩尔分数）的Fe-Ni合金中，相应的铁磁相比例为50%～70%，居里温度分布在100～500K区间。温度升高，浓度不同，居里点也不同的铁磁相连续地从大比体积的铁磁态转变为小比体积的顺磁态，体积反常收缩。

以上各种模型均能够解释一些因瓦现象，但是由于模型中假设太多，显得这些基于定域电子模型的因瓦理论过于人为化了。而且，所有上述因瓦理论又都是以下面的条件为前题，即含铁面心立方结构和原子的（或磁性的）不均匀性。因此可以说，定域电子模型是有它的局限性的。

2.巡游电子模型

基于巡游电子模型的斯通纳（Stoner）能带理论，许多人对因瓦问题进行了深入的研究。具体机制可分为以下几种。

（1）能带模型

认为交换作用使电子极化，并使不同极化方向的能带移位，电子动能和能态密度增大，能态宽度减小，这样导致点阵常数和体积增大，产生自发体积磁致伸缩。

（2）巡游电子弱铁磁性理论

巡游电子弱铁磁性材料都具有低居里点和低磁矩或不稳定磁有序的共同特点。由于这类材料的交换劈裂很小，可把自由能展开成级数，从而可以解释因瓦材料中的许多磁性反常和热膨胀系数很小的现象。

除上面介绍的几种因瓦理论模型外，也还有其他的理论模型。