热膨胀系数与其他物理量的关系

1.热膨胀系数与热容、温度的关系

热膨胀是固体材料受热以后晶格振动加剧而引起的体积膨胀，而晶格振动的激化就是热运动能量的增大。升高单位温度时能量的增量也就是热容的定义。所以热膨胀系数显然与热容密切相关并有着相似的规律。格留涅申（Gruneisen）从晶格振动理论推导出金属热膨胀系数与热容间的关系式（称为格留涅申关系式）为

式中，α_V为体胀系数；C_V为质量定容热容（也叫比定容热容）；K是体积模量；r为格留涅申常数，表示原子非线性振动物理量，对一般物质在1.5与2.5之间变化；ν是比体积。

从热容理论可知，在低温下C_V随温度的变化遵从T³关系，所以在低温下膨胀系数随温度的变化也应服从T³规律，即膨胀系数与温度关系曲线同热容与温度关系曲线特征一致。实验结果也是如此，如图4-15所示，图中T_s为熔点。

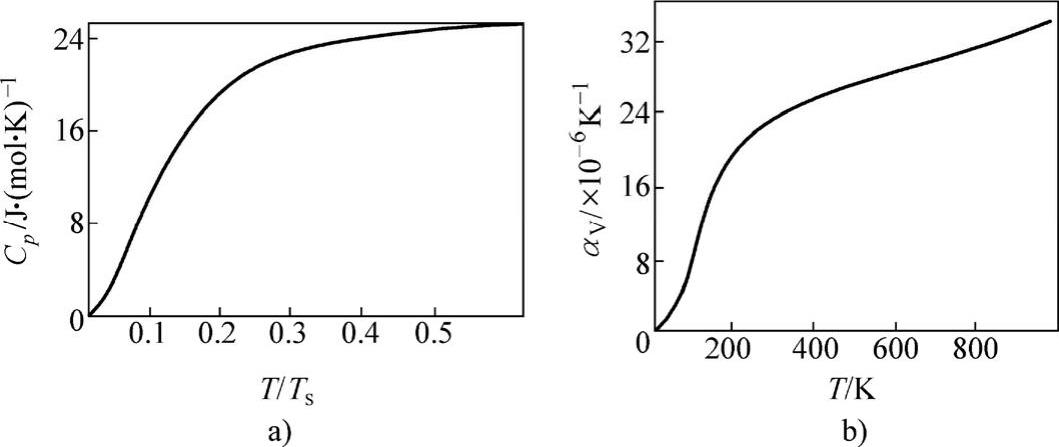
图4-15 Al的摩尔定压热容与温度的关系（图a）及体胀系数与温度的关系（图b）

由式（4-68）还可以看出，膨胀系数与比体积成反比。钢铁材料的γ-Fe的比体积比α-Fe的小，因而加热时γ-Fe膨胀比α-Fe强烈。

2.热膨胀系数与结合能、熔点的关系

由于固体材料的热膨胀与晶体点阵中质点的位能性质有关。质点的位能性质是由质点间的结合力特性所决定的。质点间结合力很强，则位阱深而狭窄，升高同样的温度差，质点振幅增加得较少，故平均位置的位移量增加得较少，因此，热膨胀系数较小，如表4-1所示。

表4-1 热膨胀系数与结合能熔点的关系

(www.xing528.com)

格留涅申还提出了关于固态的体热膨胀极限方程。方程表明，一般纯金属温度由0K加热到熔点T_s，体胀为6%。当固体加热体积增大6%时，晶体原子之间的结合力已经很弱，因而使固态熔化变为液态。同时还可看出，物体熔点愈低，则该物质的膨胀系数愈大；反之，物体的熔点愈高，则该物体的膨胀系数愈小。这是因为在温度0K到熔点温度T_s区间，固体体积的变化总量都是6%之故。元素的平均线胀系数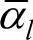与熔点T_s间的经验公式为

式中n=1.17，对于金属A=7.24×10^-2。从该式可以看出，元素的膨胀系数愈小，则它的熔点就愈高。

3.热膨胀系数与德拜温度的关系

前面已经叙述，由林德曼公式可以导出Θ_D与熔点T_s的关系：Θ_D=137[T_s/（mV²/3）]¹/2，若式（4-69）中n=1，那么可得到热膨胀系数与德拜温度的简单关系

因为熔点T_s和德拜温度Θ_D表征晶体原子间结合力（结合能），而从式（4-69）、式（4-70）不难看出了膨胀系数与原子间结合力成反比。因此，表征原子间结合力的物理量如E、T_s、Θ_D都与热膨胀系数有关。固体的弹性模量、熔点、德拜温度愈高，则热膨胀系数愈低。

4.热膨胀系数与热导率的关系

弗兰克尔确定了非金属的热膨胀系数平方应正比于热阻率ω′，即

式中，λ是热导率；C是常数。