晶格振动的非谐效应——揭示热膨胀的本质

如果晶体中的振动是严格的简谐振动，晶体将不会因受热而膨胀。这里只以双原子分子为例，先定性地讨论热膨胀问题，所得结果可以直接应用于一维晶格，如图4-14所示，假定左边的原子固定不动，而右边的原子可以自由地振动。如果势能曲线对原子的平衡位置对称，则当原子振动后，其平均位置将和振幅的大小无关，如果这种振动就是热振动，则两原子间的距离将和温度无关。实际上，两原子之间的互作用势能曲线并不是严格的抛物线，而是不对称的复杂函数，如图4-14中所示。平衡位置的左边较陡，右边较平滑，因此当原子振动后，随着振幅（或总能量）的增加，平均位置将向右边移动。例如，当振动的总能量为某一个E_i时，平均位置移至p_i。与各个能量相应的平均位置如图4-14中的AB曲线所示。物体的热膨胀就是由于势能曲线的这种不对称性所导致。

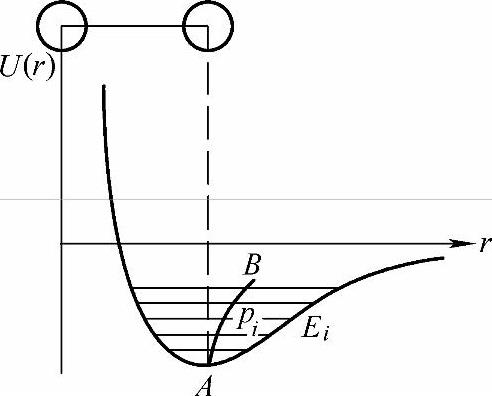
图4-14 原子间互作用势能曲线

以下用经典的方法计算平均位置向右边移动的距离。设r₀是原子的平衡位置，δ是离开平衡位置的位移。把原子在r₀+δ点的势能U（r₀+δ）对平衡位置r₀按式（4-1）展开，则

第一项为常数，第二项为零。如果取U（r₀）=0，并令式（4-61）右边第三项中δ²的系数为f，第四项中δ³的系数为-g，忽略δ³以上各项，那么式（4-61）变成

根据玻耳兹曼统计，原子的平均位移δ为

式中k为玻耳兹曼常数。(www.xing528.com)

如果在势能的展开式中只保留δ²项，即假定力是准弹性的，振动是简谐振动，则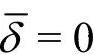，即原子的平均位置和平衡位置相同，没有热膨胀现象发生。如果计入非对称项，则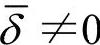，设δ很小，则式（4-63）的分子可写成

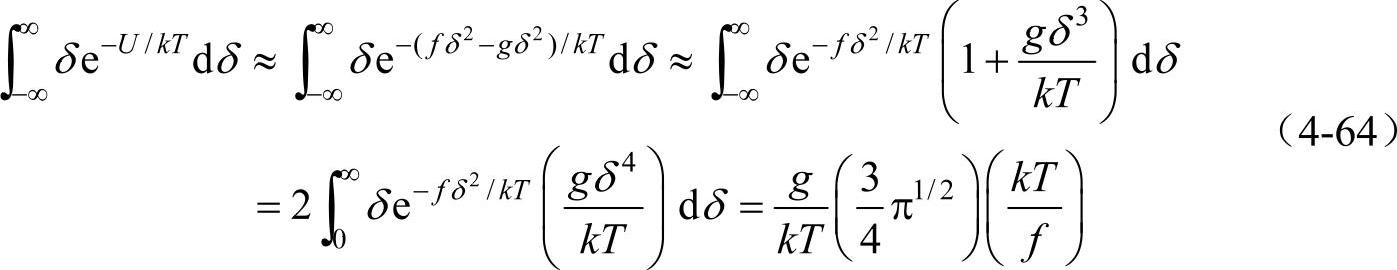
同时，式（4-63）的分母可写成

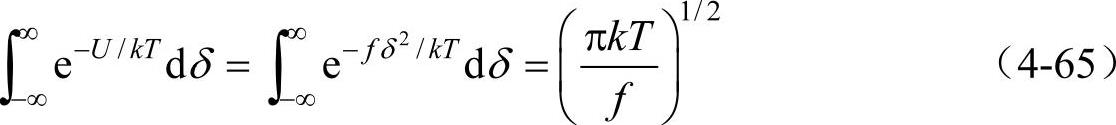
将式（4-64）和式（4-65）代入式（4-63）得

因此得到线胀系数α为

显然，α是一个与温度无关的常数。如果计入U（r₀+δ）展开式中的更高次项，则线胀系数α将和温度有关。