量子理论解析晶态固体的热容性质

根据晶格振动的量子化概念导出的的三维晶格系统的总能量E的公式（4-39）及量子平均数公式（4-45），可以导出该晶体的摩尔定容热容C_V，m（N个原胞，每个原胞有个l原子）为

这就是按照量子理论求得的摩尔定容热容表达式。但是由上式计算C_V，m必须知道谐振子的频谱。这是非常困难的事。实际上，采用简化的爱因斯坦模型和德拜模型。

1.爱因斯坦模型

爱因斯坦提出的假设是：每一个原子都是一个独立的振子，振子的能量是量子化的。振动产生的声子为玻色子。原子之间彼此无关，并且都是以相同的角频率振动。根据式（4-48），而ω_j（q）=ω（j=1，2，3，…。每个振子的频率相同），Nl=N_A（总原子数），因此晶体的摩尔定容热容为

定义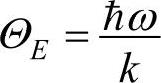为爱因斯坦温度。求晶体的摩尔定容热容时，N_A=N₀，N₀k=R。晶体的摩尔定容热容C_V，m为

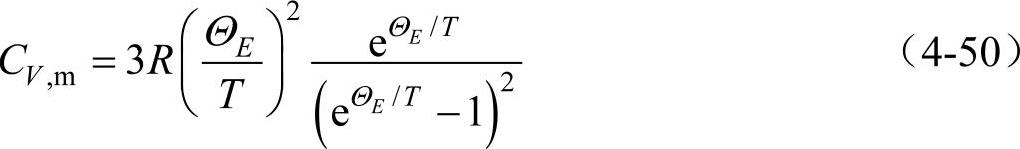
式（4-50）称为爱因斯坦量子摩尔热容公式，它表明的摩尔热容与温度的关系和实验结果有更一步的接近。大多数固体的Θ_E值在100～300K的范围内。Θ_E可由实验确定，即在100～300K范围内，对应一个温度测出一个C_p，m值，再换算成C_V，m值代入式（4-50），即可求出Θ_E。许多简单固体的摩尔热容大体符合式（4-50），所以可以认为这个理论在一级近似上描述了晶体的摩尔热容。例如，金刚石的实验数据与爱因斯坦理论曲线符合得很好。

从爱因斯坦摩尔热容模型式（4-50）可以得出①当高温时，T》Θ_E，则Θ_E/T《1，。所以

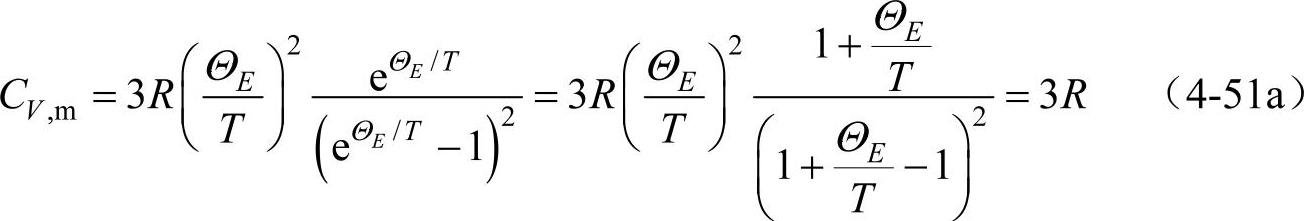
这就是杜隆—珀蒂定律，也就是实验曲线图4-8的Ⅲ区的情况。说明在高温时，爱因斯坦模型同经典热容理论和实验结果符合得很好。这是很好理解的，因为在高温区，振子的能量近似等于kT，而kT远大于能量量子（ћω）时，量子化效应就可以忽略，所以给出这个结果与高温区的热容实验结果符合。②当低温时，T《Θ_E，则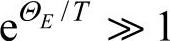，所以

由上式可见，C_V，m与T的关系的趋势是符合实验情况的（图4-8的Ⅰ区），如图4-9所示，这是经典理论所不能得到的结果。但C_V，m与T呈指数关系变化，而试验的C_V，m与T呈三次方的关系变化。

③在温度中温区域（图4-8的Ⅱ区），爱因斯坦模型比实验值下降的快，如图4-9所示。

爱因斯坦模型的结果，在有些区域与实验不符。其原因是假设与实际情况不符。实际晶体质点间是互相联系的，这种联系在低温下表现得尤其显著，格波振动的频率也是有差别的。

2.德拜热容模型

德拜考虑晶体中点阵格点间的相互作用。其主要观点是：晶格的每个谐振子不是相互独立的，而是互相联系的，把格波看成弹性波（不考虑光学波）。每个谐振子的频率不同，频率范围从零到某一最大值ω_m。

图4-9 爱因斯坦模型与实验曲线的比较

由式（4-48）可知，一个振子对摩尔定容热容的贡献为

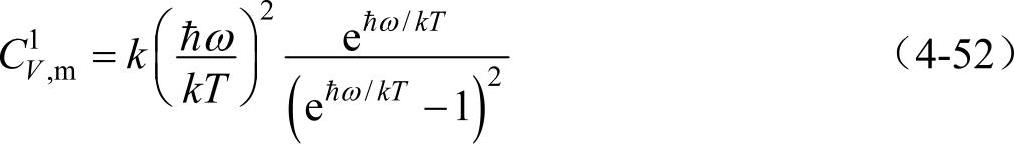
现在考虑到ω不同，若ρ（ω）dω为1mol原子晶体频率位于ω与ω+dω之间的振子数，则所有振子对热容的贡献就变成对式（4-52）积分的形式

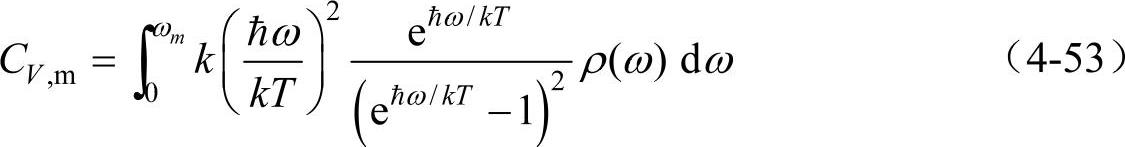
定义，称为德拜温度。由此得到德拜热容模型

(www.xing528.com)

式中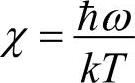。ΘD与Θ_E类似，物质不同Θ_D不同，如Na、Ti、Al、金刚石分别为、158K、420K、428K、2230K。

从德拜热容模型式（4-54）可以得出：

①当高温时，T》Θ_D，则eχ≈1+χ，所以

这就是杜隆—珀蒂定律，也就是实验曲线图4-8的Ⅲ区的情况。说明在高温时，德拜热容模型同经典热容理论和实验结果符合。

②当低温时，T《Θ_D，则

对一定的物质有一定的Θ_D，所以，C_V，m与T³成正比，它与实验符合。这比爱因斯坦理论更进一步了。

③在温度中温区域（图4-8的Ⅱ区），德拜模型的值与实验结果也符合得很好。这也说明在一般温度下，晶体温度升高时所吸收的热量，主要来加强晶格振动。

上面所述的符合仍是大致上的，将德拜模型的值与实验结果严格对照如图4-10所示。在图4-8的Ⅰ区，T<5K，实验值C_V，m与T成正比；在Ⅲ区，实验值C_V，m虽然很接近25J/（mol·K），但并不是以3R为渐近线，而是超过3R继续有所上升。其原因是德拜热容模型只考虑了晶格振动对热容的贡献，但实际上，自由电子对热容也有部分贡献，热容的电子贡献部分在极高温度（对普通金属要几万度）及近于0K的极低温度下才是显著的。

德拜温度Θ_D与晶体的热容、原子间的结合力、晶体的熔点、弹性模量、温度因子都有关系。它与低温摩尔定容热容的关系如上面导出的式（4-56）。式（4-5）中，原子间的恢复力系数β（反映原子间的结合力）与简谐振动角频率ω²成正比，爱因斯坦温度Θ_E与ω成正比。一般情况下，Θ_E=0.7Θ_D，因而β正比于Θ_D²；一般认为在熔点T_s时，原子的振幅达到使晶格破坏的数值，这样原子振动的最大频率ω_m和熔点T_s间有林德曼（Lindlman）公式：ω_m=2.8×10¹²[T_s/（mV²/3）]¹/2，m为原子质量，V为原子体积。由林德曼公式可以导出：Θ_D=137[T_s/（mV²/3）]¹/2；晶体的弹性模量E正比于β，当然也正比于Θ_D²。

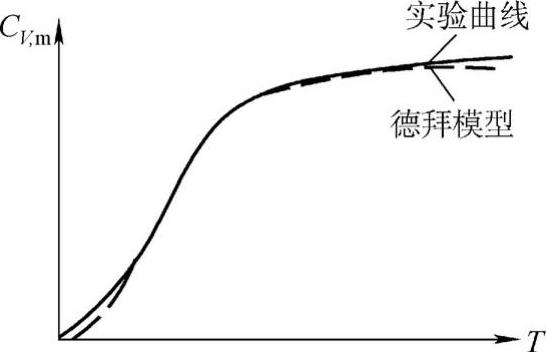
图4-10 德拜热容模型与实验曲线的严格对比

3.德拜热容模型与爱因斯坦模型本质区别及晶格热容与电子热容的关系

温度愈低，德拜热容模型近似愈好。因为在非常低的温度下，只有长波格波的激发是主要的。对于长波，晶格是可以看做连续介质的。

现在可以说明爱因斯坦模型在低温下与实验符合不好的原因。这个模型主要适用于光学波，光学波的ω随q变化很小，可以假设ω为常量。但是，低温下，光学波的量子化能量大于kT，因此没有被激发。这个模型忽略了非常低频的声学波，由于低频声学波量子化能量很小，在非常低温下，它们也能吸收热量而被激发，对摩尔热容有贡献。

尽管德拜模型是相当成功的，但是，它把各种可能格波的色散关系都用连续介质中弹性波的色散关系代替，显然会有局限性。从实验发现在很宽的温度范围内Θ_D本身是与T有关的，其变化量达10%，有时更高。为了改进德拜模型，人们应该用正确的格波色散关系代替长波近似式。

下面在德拜模型近似下，讨论晶格摩尔热容和电子摩尔热容的关系。

在晶格摩尔热容理论中的德拜温度Θ_D和在金属电子摩尔热容理论中的费米温度T_f都是经典过程和量子过程的分界限。在前一个理论中T>Θ_D适于用经典统计力学规律，T<Θ_D需要用量子统计规律。在后一个理论中，T>T_f可以用经典统计规律，T<T_f，须要用量子统计规律。但是对于电子情况，T_f在10⁴～10⁵K量级，所以实际温度总是远低于T_f的；而对晶格振动情况Θ_D在10²K量级，实际温度往往处在量子与经典重叠区内。

在金属摩尔热容测量实验中，需要知道在什么温度下晶格摩尔热容起主导作用（T³规律）。为了回答这个问题，把电子对摩尔热容的贡献e

C_V，m（Z）（1mol离子提供Zmol自由电子）除以声子对热容的贡献i

C_V，m得

当C_V^e，m（Z）=CVⁱ，m时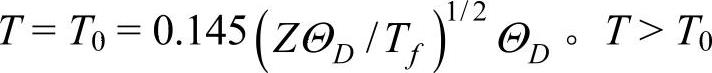，时，声子对摩尔热容的贡献超过电子的贡献。由于一般情况费米温度比德拜温度高2个量级，所以T₀只有几K，这就是金属摩尔热容与T的线性关系只有在极低温度下才能观察到的原因。